Символическое выполнение и решение ограничений

намекать:
В последнее время автор работает над автоматическим созданием тестовых примеров для программ P4 с помощью символического выполнения (Symbolic Execution) и решателя ограничений (Constraint Solver). Символическое выполнение является важным методом формальной проверки (Formal Verification) и технологией анализа программного обеспечения.
Согласно первому из 7 основных принципов тестирования программного обеспечения: Тестирование может показать наличие дефектов, но не может доказать отсутствие дефектов (Тестирование может только доказать, что в программном обеспечении есть ошибки, но не может доказать, что в программном обеспечении нет ошибок) Поэтому необходимо, чтобы программы строго доказывали отсутствие ошибок в системе путем формальной проверки (то есть с помощью математических методов).
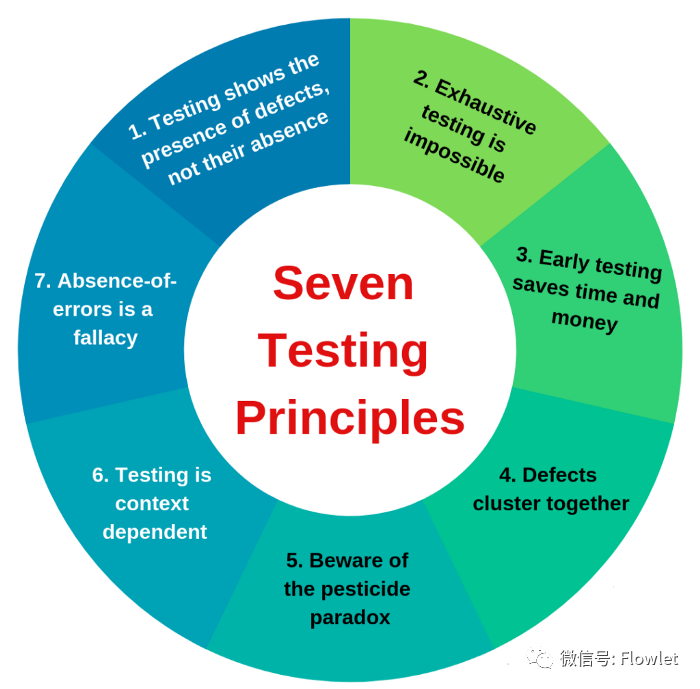
Эта статья представляет собой концептуальное обсуждение подсистем символического выполнения (Symbolic Execution) и решения ограничений (Constraint Solving) в дисциплине анализа программного обеспечения.
Эта статья в основном разделена на следующие части:
1. Символическое исполнение
Part I:Предисловие
Часть II: Классическая символическая казнь
Часть III: Развитие символической казни
Часть IV. Гибридное исполнение
Часть V. Выполнение тестов сборки
Часть VI. Выбор символического выполнения
2. Решение ограничений
Part I:Предисловие
Часть II: Решение ограничений
Часть III: Проблема решения ограничений
Часть IV: Решение проблем SAT
Часть V. Решение проблем SMT
1. Символическое исполнение

Предисловие
В качестве важного формального метода и технологии анализа программного обеспечения символическое выполнение использует абстрактные символы для замены переменных программы. Результат вычислений программы выражается как функция значения входного символа, а пространство выполнения программы пересекается в соответствии с семантикой. программа. Он играет важную роль при тестировании и верификации программного обеспечения, а также может применяться для обнаружения лазеек и уязвимостей в программах.
Символическое выполнение прошло процесс развития традиционного символического выполнения → динамического символического выполнения → выборочного символического выполнения. Динамическое символическое выполнение включает в себя гибридное тестирование и тестирование генерации выполнения.
1.1 Классическое символическое исполнение
Основная идея классического символьного выполнения заключается в использовании символических значений для замены определенных значений в качестве входных данных программы, а также в использовании символических выражений для представления значений переменных программы, связанных с символьными значениями. Когда встречается инструкция ветвления программы, выполнение программы соответствующим образом ищет каждую ветвь, и условие ветвления добавляется к состоянию программы π, сохраненному посредством символьного выполнения, где π представляет ограничения текущего пути. После сбора ограничений пути используйте решатель ограничений, чтобы проверить разрешимость ограничений и определить, достижим ли путь. Если ограничение пути разрешимо, это означает, что путь достижим, в противном случае это означает, что путь недостижим, и анализ пути заканчивается.

Возьмите пример кода на рисунке 1 в качестве примера, чтобы проиллюстрировать принцип символьного выполнения. В строке 9 программы есть ошибка. Наша цель — найти подходящий тестовый пример, который вызовет ошибку. Если вы используете метод случайной генерации тестовых примеров для выполнения конкретного тестирования программы, существует 232 значения для целочисленных входных переменных x, y и z. Значения x, y и z генерируются случайным образом. в качестве входных данных для проверки программы, вероятность возникновения ошибок программы меньше. Обработка символического выполнения заключается в использовании символических значений вместо конкретных значений. В процессе символического выполнения механизм символического выполнения всегда сохраняет информацию о состоянии. Эта информация о состоянии выражается как (pc, π, σ), где:
1) pc указывает на следующий оператор программы, который необходимо обработать, который может быть оператором присваивания, оператором условного перехода или оператором перехода. 2) π относится к информации об ограничении пути, которая выражается в виде условных ветвей, которые необходимо пройти для выполнения определенного оператора программы, и выражения символического значения α_i в каждой ветке. В ходе анализа оно изначально определяется как π=истина. 3) σ представляет собой совокупность символьных значений, относящихся к переменным программы, включая выражения, содержащие конкретные значения и символические значения αi.

Алгоритм символьного выполнения конкретно показан в алгоритме 1.
Во-первых, поскольку x, y, z являются входными данными программы, значения x, y, z определяются как символьные переменные σ: α, β, γ, и поскольку ни один условный переход еще не был выполнен, начальный состояние — σ: {x→α,y→β,z→γ};
Здесь следует отметить, что в дополнение к x, y и z, которые изначально определены как символьные переменные, если во время выполнения кода происходят операции присваивания, связанные с x, y и z, необходимо также учитывать вновь сгенерированные переменные. как символьные переменные для обработки. Например: предположим, что между 2-й и 3-й строками кода добавлена операция присваивания, даже если w=2*x, соответствующая w также будет считаться символьной переменной, поэтому состояние программы станет σ:{x→α , y→β,z→γ,w→2*α} π=истина.
Когда программа анализирует оператор решения первой ветви, если x>0, она разветвляется на два пути, а именно истинный путь и ложный путь. Из этой ветви выходят два состояния анализа, а именно, если x>0 → σ:{x→. α,y→β,z→γ} π:α>0 и если x≤0 → {x→α,y→β,z→γ}; с
Во-первых, продолжайте поиск по истинному пути, то есть, если встречается x>0, будет встречено второе решение ветви, если y<5. Из этой ветви будут сгенерированы еще два пути, и состояния пути будут такими, если y<. 5→σ: {x→α,y→β,z→γ};π:α>0∩ β<5 и если y≥5→σ:{x→α,y→β,z→γ}; π:α≤0∩β≥5, запишите статус ложного пути и оцените, встретив ли он третий путь; ветвь y+z>0 порождает два пути и два новых состояния, если y+z>0→σ:{x→α,y→β,z→γ}; β<5 ∩ y+z>0} и если y+z≤0→σ:{x→α,y→β,z→γ};
На этом этапе операции, связанные с символьными переменными, обработаны, и вам необходимо использовать решатель SMT для решения, удовлетворяющего ограничениям каждого пути. Полученное решение представляет собой тестовый пример, выполняемый по пути. Например, окончательное решение пути, если y+z>0, должно удовлетворять: α>0 ∩ β<5 ∩ y+z>0. Одним из полученных решений может быть α=1, β=2, γ=. 1. Этот тестовый пример. Результат, полученный при выполнении программы, равен a=-2, b=1, c=2. После выполнения этого пути символическое выполнение продолжается по ложному пути, если. y+z≤0 используется для проверки решения. Условие ограничения: α>0 ∩ β<5 ∩ y+z≤0. Полученное решение может быть α=1, β=2, γ=-3, а результат — α=1. это а=-2, б= 0, с=2. По аналогии, после выполнения двух путей третьей ветки, состояние, записанное во второй ветке, будет извлечено из сохраненного состояния, и будет сгенерирован тестовый пример для тестирования программы.
В принципе, традиционное символьное выполнение может полностью охватить путь программы и генерировать тестовые примеры, соответствующие пути для каждого пути.

Дерево выполнения программы примера кода показано на рисунке 2.
В программе имеется 3 точки решения ветвления и всего 6 путей. То есть механизму символического выполнения необходимо решить ограничения 6 раз и получить тестовые примеры для 6 путей. Среди них тестовый пример, полученный путем решения ограничения x≤0 ∩ y<5 ∩ y+z>0, результат выполнения — a=0, b=1, c=2, что приведет к ошибке программы.
1.2 Разработка символического исполнения
По состоянию развития символическое исполнение можно разделить на классическое символическое исполнение, динамическое символическое исполнение и выборочное символическое исполнение. Классическое символическое исполнение фактически не выполняется, а основано на синтаксическом анализе программ и имитирует выполнение через символьные значения; динамическое символическое исполнение использует комбинацию конкретного исполнения и символического исполнения, сочетая в себе преимущества конкретного исполнения и классического символического исполнения, а также появляется гибридное исполнение ( Существует две технологии символического выполнения: concolic-выполнение) и тестирование генерации выполнения; выборочное символическое выполнение может символически выполнять те части, которые интересуют программиста, а другие части выполняются с использованием реальных значений. Типичным инструментом является S2E.
Гибридное исполнение было предложено Годфруа и Сеном в 2005 году. Сен подробно остановился на его принципах и обобщил улучшения и разработки за последние десять лет. Тестирование генерации выполнения было предложено Кадаром и др. В 2006 году оно было получено в инструментах реализации EXE и KLEE. Выборочное символическое выполнение было предложено Чипуновым и др. в 2009 году и реализовано в рамках S2E.
1.3 Гибридное исполнение
Гибридное исполнение — это метод тестирования программного обеспечения, который сочетает в себе конкретное и символическое выполнение и является разновидностью динамического символьного выполнения. Основная идея состоит в том, чтобы выполнить программу с определенными входными данными. Во время работы программы ограничения пути собираются с помощью инструментов программы, путь программы ищется последовательно, а решатель ограничений используется для решения набора ограничений, собранного в предыдущем шаге. выполнение, тем самым получив тестовый пример для следующего выполнения после следующего выполнения, выберите одну из точек принятия решения в соответствии с определенной стратегией, чтобы выполнить инверсию ограничений, чтобы получить новый набор ограничений, а затем использовать решатель ограничений для ее решения; получить следующий результат выполнения. Повторяя этот процесс, вы можете избежать выполнения повторяющихся путей и тем самым добиться высокого покрытия тестами с использованием как можно меньшего количества наборов тестов.
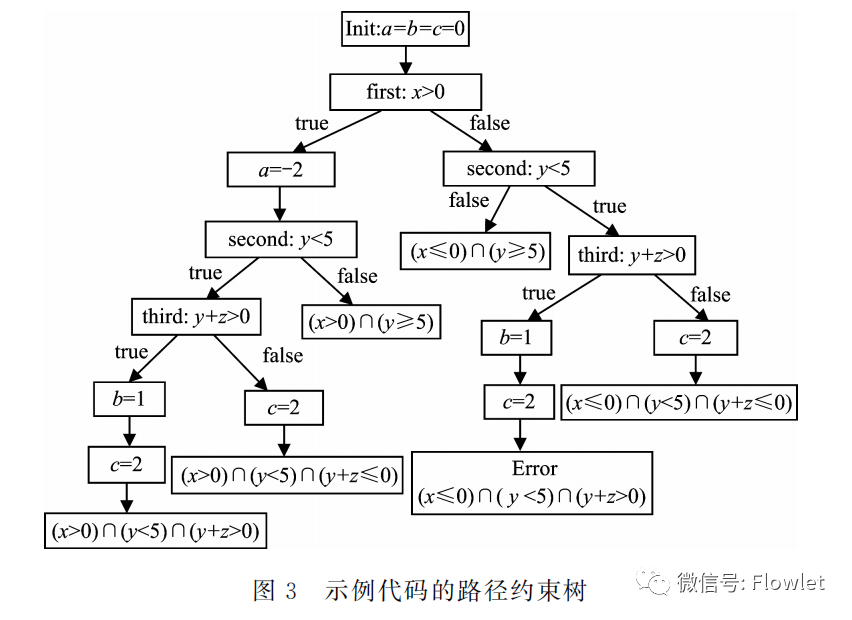
Возьмите пример кода, приведенный на рисунке 1, в качестве примера, чтобы объяснить процесс гибридного тестирования. На рисунке 3 показано дерево ограничений путей программы. Видно, что программа имеет всего 6 различных путей, и каждому пути соответствует соответствующий набор ограничений. Из дерева ограничений путей видно, что код имеет 5 путей, которые заканчиваются нормально, и 1 путь с ошибкой. Траектория выполнения программы определяется с помощью набора ограничений, и программа направляется на выполнение по заданному пути. Для примера программы набор ограничений, которые могут вызвать ошибки программы, следующий: (x≤0)&(y<5)&(y+z>0),Во время выполнения программы,Соберите и сохраните ограничения, выполняющие путь. Чтобы обеспечить полный охват этого кода,,программа будет выполнена 6 раз,И каждый раз, когда оно выполняется, инвертируется новое ограничение, а затем решается новый вариант использования.,ктестдругойпуть。
Например, выберите начальные настройки тестового входа. x=y=z=1. В конкретном процессе выполнения, поскольку 1>0, будет выполнено a=-2, тогда, поскольку 1<5 и 1+1>0, будут выполнены b=1 и c=2; . Программа завершается нормально, и ограничения, собранные на пути во время выполнения, (x>0)&(y<5)&(y+z>0)。Чтобы обеспечить следующее выполнение для покрытияпрограммаразницапуть,Смешанный тест использует определенную стратегию для выбора одного из условий оценки ветвления для отрицания.,т.е. инвертировать ограничения, собранные при предыдущем выполнении,Получить новый набор ограничений(x>0) ∩ (y<5) ∩ (y+z≤0), новый тестовый пример получается путем решения этого ограничения x=1, y=1, z=-2 используйте вновь созданный тестовый пример для выполнения программы, и процесс выполнения выглядит следующим образом; a=-2,c=2, результат выполнения a= -2, b=1, c=2, программа завершается нормально.
После этого раунда работы новых ограничений нет, поэтому набор ограничений равен (x>0) ∩ (y<5) ∩ (y+z≤0). Следующий раунд инверсии ограничений изменит набор ограничений на (). x>0 ) ∩ (y≥5), решение генерирует новый тестовый пример как x=1, y=5, z=-2, а программа по-прежнему работает нормально и завершается.
В соответствии с этим процессом повторяется конкретное выполнение и сбор ограничений пути, а также процесс инверсии ограничений для создания новых тестовых случаев. После решения набора ограничений (x≤0) ∩ (y<5) ∩ (y+). z>0), тестовый пример получается. Когда x=-1, y=1, z=2, результат выполнения равен a=0, b=1, c=2, поскольку a+b+c=3, поэтому возникнет ошибка в строке 9 программы.
Используя гибридное тестирование для проверки правильности программы, теоретически можно полностью охватить путь программы. Однако по мере увеличения количества ветвей пространство состояний программы растет в геометрической прогрессии. В сочетании с ограничениями решения ограничений гибридное тестирование не может. использоваться в реальном программном обеспечении. С тестируемым приложением все еще существуют некоторые проблемы. Например, основная идея гибридного конколического тестирования, предложенная Рупаком и др., заключается в тестировании программы путем объединения методов случайного тестирования и гибридного тестирования, чтобы обеспечить широту и глубину поиска в пространстве состояний программы. Этот метод сочетает в себе преимущества исчерпывающего и тщательного смешанного тестирования и быстрого и эффективного случайного тестирования, улучшая охват тестирования программы.
1.4 Выполнение тестов сборки
Тестирование генерации выполнения — это также технология тестирования программного обеспечения, сочетающая в себе конкретное и символическое выполнение. Оно было предложено Кристианом и др. из Стэнфордского университета и реализовано в EXE. Самая большая разница между выполнением сгенерированных тестов и смешанными тестами заключается в способе смешивания символического и конкретного выполнения. Тест генерации гибридного выполнения заключается в использовании конкретного выполнения для сегментов кода, не связанных с символическими переменными, при выполнении программы и выполнении символического выполнения для сегментов кода, связанных с символьными переменными, используя символическое выполнение для управления процессом тестирования и создания тестового примера для каждого пути; и выполните его один раз.
Основная идея выполнения сгенерированных тестов заключается в автоматической генерации потенциально очень сложных тестовых случаев с помощью программного кода. В процессе выполнения программы с использованием символьного ввода информация о состоянии ложного пути записывается в ветви, и ветвь оценивается. быть правдой продолжает выполняться. Запишите информацию об ограничениях и получите тестовые примеры пути, решив эту информацию об ограничениях. Процесс анализа заключается в выполнении сгенерированного теста.
Ниже приведен пример кода на рис. 1 в качестве примера, иллюстрирующего процесс выполнения сгенерированных тестов.
1) Установите начальное состояние: задайте x, y, z как символьные переменные и примите любое значение. Поскольку типы x, y, z являются целыми числами, их значения могут быть ограничены между INT_MIN и INT_MAX, поэтому добавьте ограничения: x, y, z≥ INT_MIN ∩ x, y, z≤ INT_MAX, выполните программу символьного ввода .
2) Выполнение разветвления на первой условной ветви, строка 3, и устанавливает ограничение для истинной ветви на x>0, а ограничение x на ложную ветвь — на x≤0. Выберите истинную ветвь, чтобы продолжить выполнение, а ложная ветвь клонируется и сохраняется в виде стека.
3) Выполнение разветвления на второй условной ветви (строка 4), установите ограничение для истинной ветви равным x>0 ∩ y<5 и установите ограничение x для ложной ветви равным x>0 ∩ y≥5. Выберите истинную ветвь, чтобы продолжить выполнение, и ложную ветвь, чтобы клонировать и сохранить.
4) Выполнение вилки на третьей условной ветви (строка 5), установите ограничения на истинную ветвь как x>0 ∩ y<5 ∩ y+z>0 и установите ограничения на ложную ветвь как: x>0 ∩ y<5 ∩ y+z≤0. Выберите истинную ветвь, чтобы продолжить выполнение, и ложную ветвь, чтобы клонировать и сохранить.
5) Поскольку истинная ветвь не удовлетворяет ограничению a+b+c=3 в строке 7, она выполняется до тех пор, пока программа не завершится (строка 10), а символическое ограничение x>0 ∩ y<5 ∩ y+z> 0 решается для получения первого тестового примера.
6) Заканчивается выполнение истинной ветки, и записи ветвей последовательно извлекаются из хранилища клонов. Первой вынимается ветвь с условием ограничения x>0 ∩ y<5 ∩ y+z>0. Второй тестовый пример получается его решением.
7) Поочередно извлекайте записи ветвей из резервной копии клона и решайте, чтобы получить тестовые примеры, пока стек записей ветвей не станет пустым, и получите тестовые примеры для всех путей. Одна из ветвей будет выполнена с кодом ошибки (строка 9). Ограничение ветвления в этот момент равно x≤0 ∩ y<5 ∩ y+z>0. Решите это ограничение, чтобы получить тестовый пример, вызвавший ошибку.
По сравнению со смешанным тестированием преимущество выполнения сгенерированного тестирования состоит в том, что оно позволяет получать всю информацию о путях и соответствующих тестовых примерах более систематически и эффективно, избегая повторяющихся процессов поиска. Его недостатком является то, что оно потребляет много памяти. многопоточность вместо хранилища ветвей для достижения одновременного поиска в нескольких ветках и генерации тестовых примеров.
1.5 Выборочное символическое исполнение
Символическое выполнение, ограниченное проблемами расширения путей и решения ограничений, не подходит для ситуаций, когда размер программы велик или логика сложна, и не существует хорошего решения для программ, которые больше взаимодействуют с внешней средой выполнения. Выборочное символическое исполнение — это технология анализа символического исполнения, возникшая для решения таких проблем. Это также технология анализа, которая сочетает в себе конкретное исполнение и символическое исполнение. На основе конкретного анализа решено переключиться между символическим исполнением и конкретным исполнением. При выборочном символьном выполнении пользователи могут указать любую интересующую часть всей системы для анализа символьного выполнения, которая может включать приложения, файлы библиотек, ядро системы и драйверы устройств. Выборочное символическое исполнение плавно переключается между символическим и конкретным исполнением и прозрачно преобразует символическое и конкретное состояния. Выборочное символьное выполнение значительно повышает удобство использования символьного исполнения в практических приложениях для крупномасштабного аналитического тестирования программного обеспечения и устраняет необходимость в имитационном моделировании этих сред.
Символьный поиск выборочного символьного выполнения в пределах указанной области является полным символьным выполнением, а специфическое выполнение используется за пределами этой области. Основная задача выборочного символьного выполнения — перед анализом разделить большие программы на конкретные области выполнения и области символьного выполнения. Эта избирательность относится к выполнению символического выполнения только в необходимых областях и является ключевым элементом масштабирования практических прикладных систем до масштаба, доступного для символического выполнения.
Аналогичным образом возьмем пример кода на рисунке 1 в качестве примера, чтобы проиллюстрировать принцип выборочного символьного выполнения. Предполагается, что символически анализируются только сегменты кода в строках 4-7 кода, а остальные части выполняются конкретно. Ядром выборочного символьного исполнения является интерактивная обработка символьного исполнения и конкретного исполнения, то есть обработка, когда конкретное исполнение переходит в область символического исполнения и когда символическое исполнение переходит в конкретное исполнение.
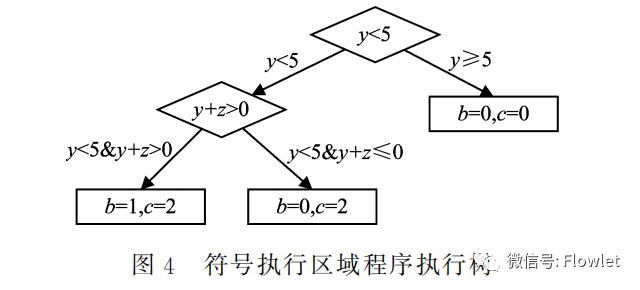
Выполните символьный анализ выделенного фрагмента кода, символическими переменными которого являются только y и z, а x должно быть только конкретным значением. Предполагая, что случайно сгенерированные начальные входные данные равны x=0, y=0, z=0, выполнение программы приведет к a=0, b=0, c=2. Когда код выполняется в области символьного выполнения, будут выполняться преобразования 0 → y и 0 → z, а также выполняться символьный анализ. Дерево выполнения программы этой области кода показано на рисунке 4.
Символический анализ в этой области кода соответствует процессу символического анализа всей программы. На основе различной информации об ограничениях можно генерировать различные тестовые примеры для выполнения целевой программы. После выполнения 7-й строки кода символические переменные. y и z Преобразуется в определенное значение, т.е. y→0и z→0, продолжайте конкретно выполнять оставшийся код, тогда это выполнение завершается. Далее по результатам символьного анализа случайные пары x Получите значение и сгенерируйте тестовые примеры, например x=2, y=6, z=0, результат выполнения программы a=-2, b=0, c=0, ошибка программы не возникает, и тест продолжает генерироваться, например x=-1, y=2, z=-3, выполнить программу, решить и выполнить тестовые примеры различных путей в соответствии с ограничениями ветвления в области символьного выполнения, пока не будут выполнены все пути в области анализа целевого символа. потому что x Значение всегда случайно, поэтому может привести к тому, что даже если все пути в символьной области выполнения будут пройдены, в конечном итоге ошибка программы не возникнет. Только когда область символического выполнения выполняется по пути y<5 & y=z===x Стоимость просто удовлетворяет Если x<0, будет срабатывать ошибка программы, то есть триггер ошибки программы возникает только с определенной вероятностью.
Селективностьсимволическое Основная задача состоит в том, чтобы совместить это символическое и конкретное представление данных с исполнением, сохраняя при этом аналитическую правильность и эффективность. Поэтому необходимо установить четкие границы между конкретной областью и областью символа, а данные должны иметь возможность завершить преобразование между конкретными значениями диапазона значений символа, когда выполнение пересекает установленные границы области, что также даселективностьсимволическое Вклад исполнения заключается в следующем: правильное выполнение реальной системы и ее необходимых задач перехода между состояниями, достижение цели максимизации локального выполнения в определенной степени.
2. Решение ограничений

Предисловие
«Решение ограничений» обычно относится к методологии: оно подчеркивает формальное выражение проблем с помощью определенного математического языка, а затем решает их. Это обычная методология решения компьютерных задач. Следовательно, «решение ограничений» является междоменным. Когда оно упоминается в области формальных методов, обычно подразумевается проблема выполнимости, когда оно упоминается в области исследования операций, речь идет о проблемах математического программирования и когда это упоминается в области САПР, подразумевается проблема выполнимости. Это проблема геометрических ограничений.
2.1 Решение ограничений
Ограничения повсюду,Ограничения — это повсеместное понятие в реальном мире. из личной жизни,в промышленную сферу,Это отражается на национальной экономике и жизнедеятельности людей. Например: мы составляем планы путешествий,Ограничено временем и расходами школьного расписания занятий;,получать классные ресурсы,Ограничения, такие как учителя и время; продукция, обработанная на заводе, ограничена последовательностью обработки продукции и конструкцией микросхем;,с учетом функциональных требованийиограничения процессаи т. д.。
Откройте для себя ограничения в сцене, разные точки зрения:
- Факты/Правила. (Например, при нажатии кнопки открывается дверь; в сутках 24 часа; Джон — учитель Алисы)
- Должен сделать. (Например, при выходе из комнаты свет необходимо выключать)
- Чего делать нельзя. (Например, нельзя проехать на красный свет)
Когда мы говорим об «ограничениях» в жизни, мы склонны отдавать предпочтение последнему и игнорировать два других. По сути, многие проблемы учитывают три вышеупомянутые точки зрения, и ограничений почти нет.
существоватьматематикасередина,Ограничение — широкое понятие,Относится к атрибутам/отношениям, которым должно удовлетворять количество даматематики. например,x>0 даограничение,x>y является ограничением, и a∨b∨¬c также является ограничением. Задача с ограничениями часто содержит множество ограничений.
Чтобы решить ограничения, вы должны сначала выразить ограничения на математическом языке. Модель ограничений — это математический язык, используемый для выражения ограничений. Общие модели ограничений включают в себя
- Булева выполнимость или пропозициональная выполнимость (сокращенно SAT);
- математическое программирование (также известное как оптимизация исследования операций, особенно представленное смешанным целочисленным линейным программированием);
- Теории выполнимости по модулю (SMT). SMT на самом деле представляет собой логику предикатов первого порядка, ограничивающую базовую теорию;
- Проблема удовлетворения ограничений (CSP), это универсальная модель, а другие вышеприведенные модели можно назвать формой CSP.
Модель ограничений по сути является моделью даматематики. Есть также много математических моделей.,Например, дифференциальные уравнения (включая уравнения в частных производных PDE и обыкновенные дифференциальные уравнения ODE),Механика жидкости (вычислительная Fluid Динамика, CFD), геометрические ограничения и т. д. на самом деле все являются моделями ограничений. Однако по историческим и дисциплинарным причинам мы обычно ссылаемся на «Решение». ограничений, большую часть времени мы говорим о нескольких моделях и их вариантах, упомянутых выше, которые, как правило, представляют собой математическую логику и математическое программирование, иногда включая геометрические ограничения. Когда люди говорят о дифференциальных уравнениях, они, естественно, находят конкретную математическую ветвь дифференциальных уравнений, но редко находят ее в разделе «Решение». ограничений。
Каждая модель ограничений также является проблемой. Так как же отличить модели от проблем?,Почему существует только одна модель вопросов SAT?,Но если Да случайно обнаружит задачу комбинаторной оптимизации, она не будет считаться моделью? Чтобы называться моделью, задача должна иметь как минимум:
- Абстракция (математика)
- Универсальность (может выражать определенные типы нетривиальных задач)
- Решаема (или может быть решена большую часть времени в реальности),Баланс экспрессивной способности и производительности решения).
«Решение», как следует из названия, означает решение проблем. Для задач с ограничениями, выраженных на математическом языке, необходимо найти ответ на проблему. С этой точки зрения получение ответа вручную также является решением. Но алгоритмический псевдокод не является решением. Необходимо запрограммировать алгоритм и запустить программу для расчета ответа на задачу до завершения решения.
Решатель обычно относится к программе, которая может решить определенную математическую модель. «Решатель» — также широко распространенное, но менее известное понятие.
Позвольте мне сначала поговорить о чем-то, что всем знакомо, о «калькуляторе». При вводе арифметических данных, например 1+1+4*6, результат вычисляется = 26. Решатель можно рассматривать как суперкалькулятор, и по сути он решает уравнения. Его входными данными являются уравнения (математические формулы). Решатель сталкивается с различными формами математических формул, которые могут быть линейными уравнениями, такими как «x+y=4, x-y=2” ,Вы также можете создавать сложные логические формулы.,Так,“(𝑥+y>10∨3x-z=2)∧(y=f(x+z)∨y-10z≥0)∧(𝑥+y+z=6∨𝑥≤4)”。Эти входные данные обычно называются ограничениями.,И направление исследований, как решить эти ограничения,Сразуda“Решение ограничений”,Направление, укоренившееся в математике и вылившееся в промышленность.,Древнее и до сих пор сложное направление. Решатель — это компьютер, который решает эти задачи.
2.2 Проблема решения ограничений
Задачу решения ограничений можно формально выразить в виде тройки P=<V, D, C>,три его части,Значения следующие:
- V: множество переменных, выраженное как {v1, v2, …, vn};
- D: Набор диапазонов значений переменной,То есть диапазон значений каждой переменной,То есть переменнаяvi должна принимать значение в пределах своего диапазона значений di;
- C: Набор ограничений,Каждое ограничение содержит одну или несколько переменных.,нравиться ci Содержит k переменная, то ограничение dathis k о переменной коллекции k метаограничения.
Решение ограничений заключается в поиске решения на основе этой серии задач с ограничениями. Это решение удовлетворяет всем ограничениям и находится в пределах своего собственного диапазона значений. Если такое решение существует, говорят, что проблема с ограничениями выполнима, в противном случае оно является выполнимым. сказал, что эта проблема ограничений неразрешима.
В настоящее время существуют две основные теоретические модели решения проблем: решатель SAT и решатель SMT.
2.3 Решение проблем с SAT
Проблема SAT (Проблема выполнимости), наиболее типичной из которых является проблема логической выполнимости, относится к решению логического выражения, состоящего из набора логических переменных, существует ли набор значений логических переменных, таких, что булево выражение. это правда. Для задач SAT тип решаемых переменных может быть только булева типа, а проблемы, которые можно решить, представляют собой проблемы с формулами пропозициональной логики. Чтобы решить задачу SAT, задачу SAT необходимо преобразовать в формулу. форма КНФ.
Ниже приводится краткое введение в некоторые ключевые концепции решения вопросов SAT.
- логическое значениепеременная(Boolean Переменная): то есть переменная, значение которой может быть только истинным или ложным, булева переменнаяда. Основа булевой логики (аналогично). Javabooleanтиппеременная)。
- Булевы операции (Boolean Операция): операции, которые можно выполнять с логическими переменными, например логические и ∧(аналогично Java && операция), логическое значение или ∨ (Аналогично Java || Операция) и логическое значение ¬(Аналогично Явапеременная бывшая ! действовать);
- Логическое выражение (Boolean Выражение): Соедините логическую переменную через выражение логического оператора. Например, логическое выражение для логической переменнойaиb может быть да. a∧b(Аналогично Java a && b работать),a∨b(Аналогично Java a || b работать),¬a(Аналогично Java !a операций), мы можем превратить эти простые выражения в очень сложные, непрерывно выполняя операции ИЛИ и НЕ, такие как (¬a∨b)∧(a∨¬b)(Аналогично Java (!a || b) && (a || !b))。
- Дизъюнктивное: логическая операция ИЛИ. Логическое выражение, объединенное только логическим оператором ИЛИ, является разделительным предложением.
- Конъюнктив — это булева операция И. Только логические выражения, объединенные с операторами, являются союзными предложениями.
Введя приведенные выше понятия, можно дать понятие КНФ.
Конъюнктивная нормальная форма (Конъюнктивная нормальная форма) — стандартная форма формул пропозициональной логики. Она состоит из ряда дизъюнктивных предложений, соединенных конъюнктивными операциями. Напротив, дизъюнктивная нормальная форма - это еще одна стандартная форма пропозициональной формулы, которая состоит из ряда соединительных предложений, соединенных дизъюнктивными операциями.
А именно: a∧(¬a∨b)∧(a∨¬b): это конъюнктивная парадигма, и все соединения на самом внешнем уровне являются конъюнктивными операциями;
a∨(¬a∧b)∨(a∧¬b): Это дизъюнктивная нормальная форма, и все самые внешние соединения являются дизъюнктивными операциями.
В традиционном решателе SAT,Вам необходимо предоставить файл CNF, описывающий логику высказываний.,Расширение дадимакс,Затем определите все переменные ограничения в файле CNF.
2.4 Решение проблем SMT
Как анализировалось выше, решатели SAT могут решать только задачи с формулами пропозициональной логики, и в настоящее время существует множество практических прикладных задач, которые нельзя напрямую преобразовать в задачи SAT для решения. Поэтому позже была предложена теория SMT.
SMT (теории модулей выполнимости) расширены на основе задач SAT. Диапазон решений решателя SMT расширен от формул пропозициональной логики до формул, которые могут решать логику первого порядка. SMT содержит множество методов решения, и многие проблемы можно решить, комбинируя эти методы.
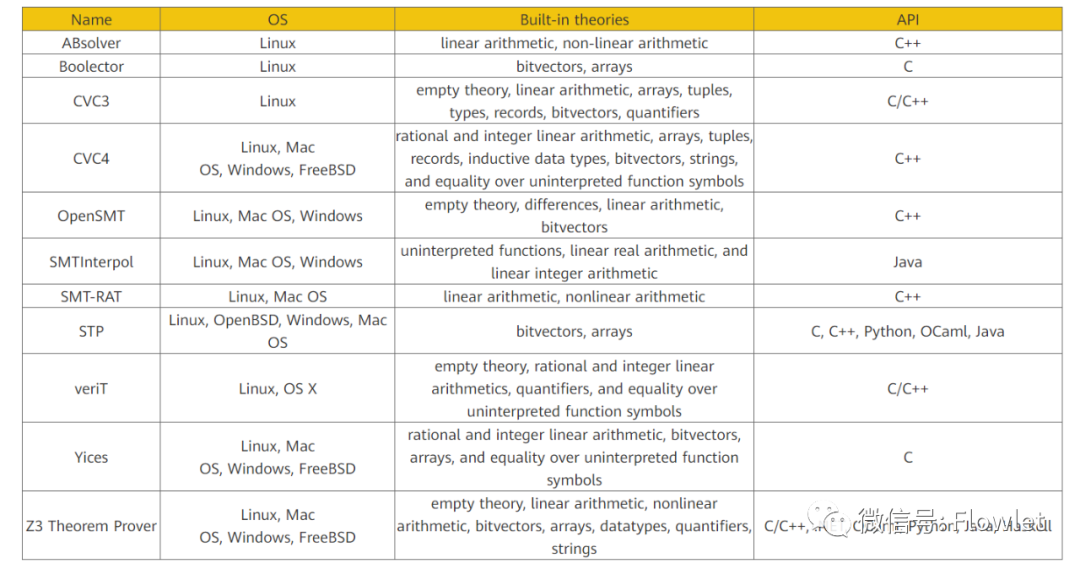
В настоящее время уже существует большое количество решателей SMT, таких как решатель Z3, разработанный Microsoft Research, решатель STP, разработанный MIT и т. д., и SMT содержит множество теорий. Например, решатель Z3 поддерживает нулевую теорию, линейные вычисления. , нелинейные вычисления и т. д. Теория линейных вычислений, битовые векторы, массивы и т. д.
Вот несколько распространенных решателей SMT (поддерживающих API основных языков программирования, таких как C/C++, Java и Python):
(Конец текста)
end
Reference:
- Обзор исследований символических казней
- Ход исследований по проблемам решения ограничений при символьном исполнении
- Решение ограничений
- Исследование по созданию вариантов использования теста на основе символического исполнения и гибридного решения ограничения.
- Введение в статический анализ кода
- Satisfiability modulo theories

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
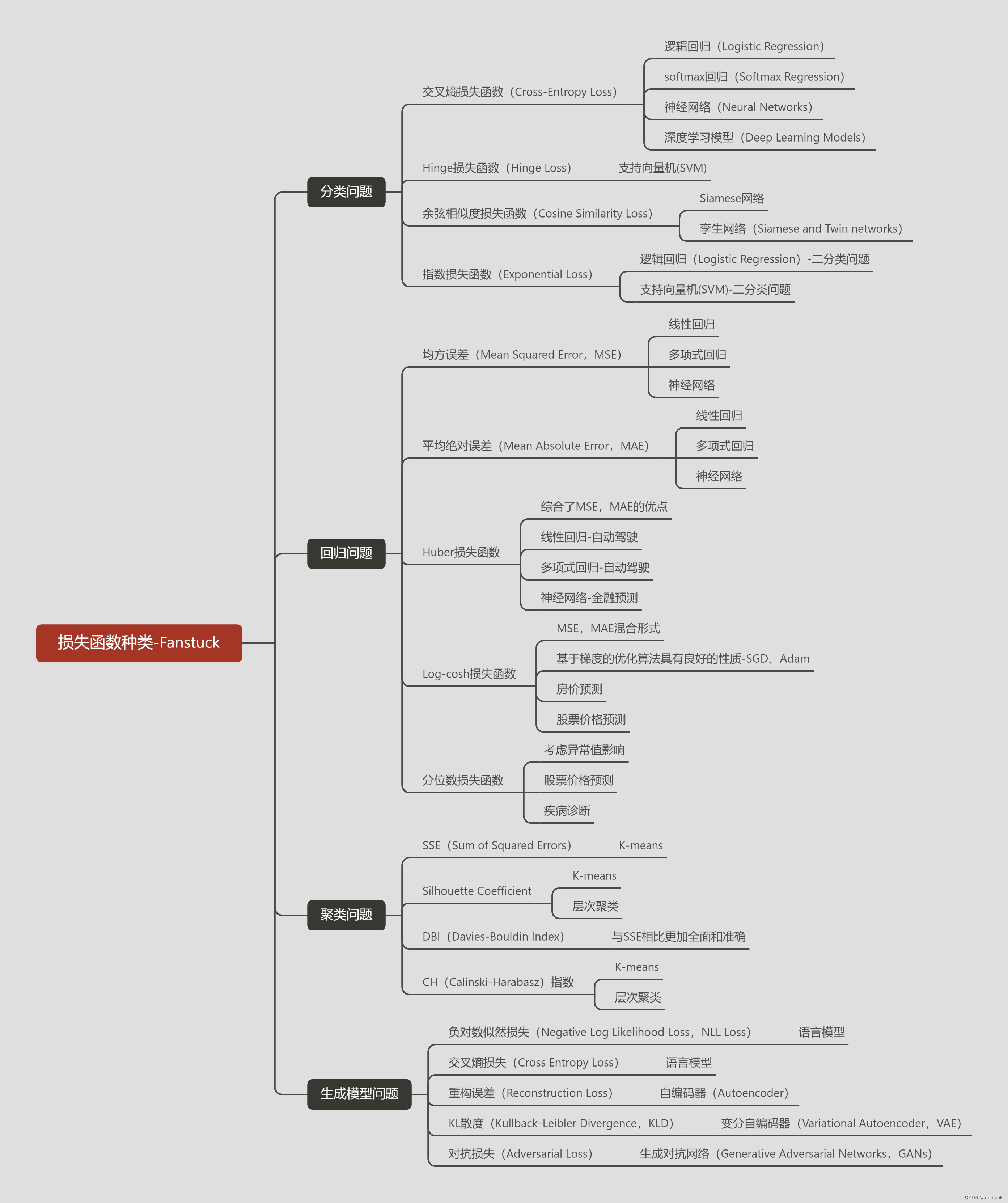
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
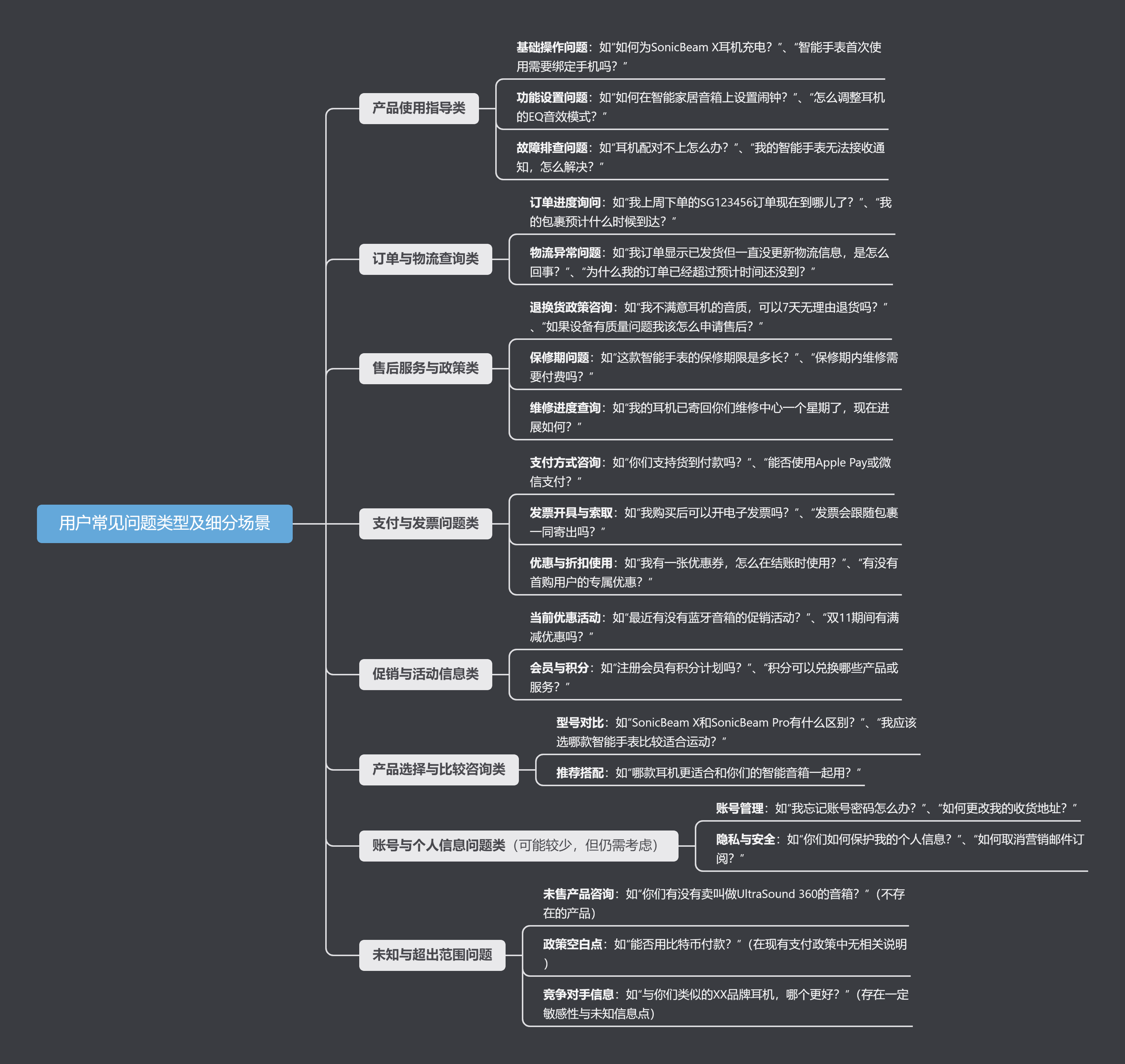
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
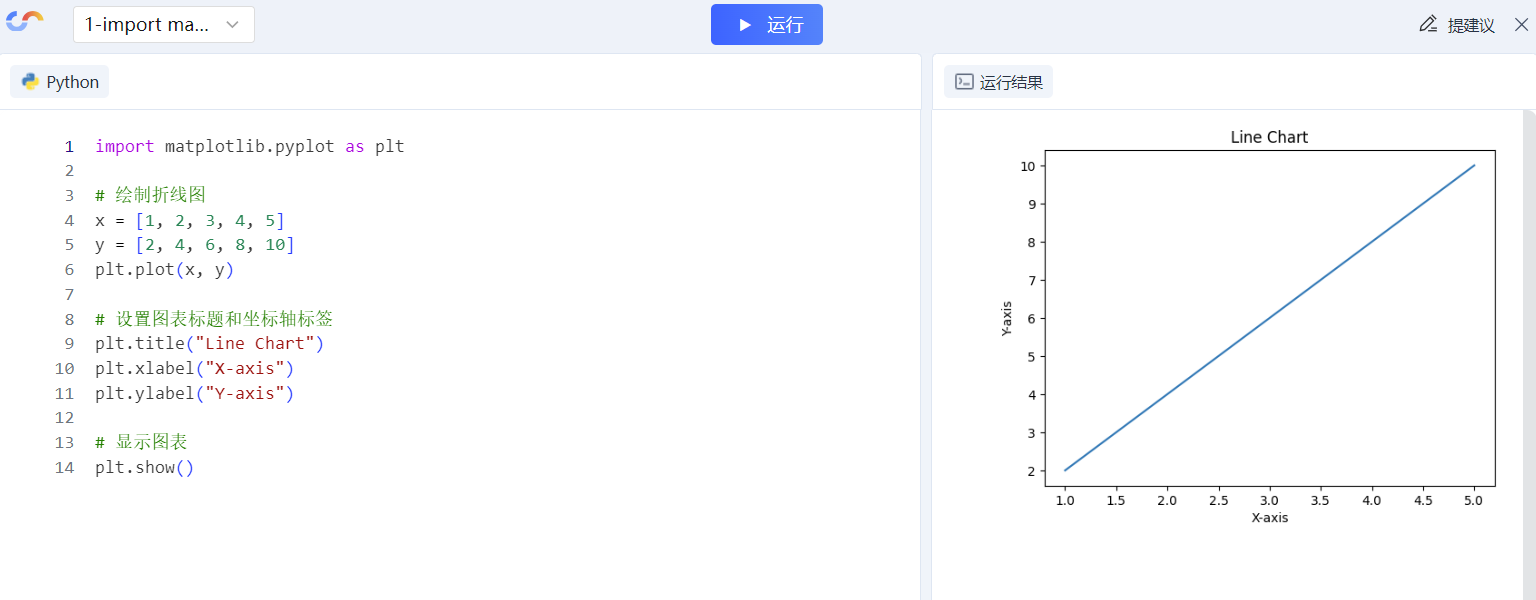
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.