Серия медитаций с асимметричным ключом (1): Обзор атак с выборочным зашифрованным текстом в режиме заполнения PKCSv1.5 по теме RSA
RSA всегда был уязвим для атак с выбранным зашифрованным текстом, главным образом из-за его гомоморфных свойств при умножении.
В этой статье в основном рассматриваются атаки Oracle на RSA в режиме заполнения PKCSv1.5.
1. Классический RSA
В качестве классического асимметричного алгоритма шифрования и дешифрования алгоритм RSA беспрецедентно реализовал концепцию «полного шифрования и дешифрования данных без прямой передачи ключа».
Алгоритм RSA основан на теории чисел, а его математический инструментарий включает функции Эйлера, модульные обратные элементы, разложение на большие простые числа и т. д., которые здесь не будут описаны.
Но стоит подчеркнуть одну вещь. Безопасность алгоритма RSA основана на сложности разложения больших простых чисел.
Чтобы сгенерировать пару ключей RSA на основе математических инструментов, вы можете обратиться к следующему примеру кода:
import random
import time
from typing import List, Tuple
from gmpy2 import gmpy2
def odd_iter():
n: int = 1
while True:
n = n + 2
yield n
def not_divisible(n):
def divide(x):
return x % n > 0
return divide
# генератор простых чисел
def primes():
yield 2
it = odd_iter()
while True:
n = next(it)
yield n
'''
https://docs.python.org/3/library/functions.html#filter
Note that filter(function, iterable) is equivalent to the generator expression
(item for item in iterable if function(item))
if function is not None and (item for item in iterable if item) if function is None.
'''
it = filter(not_divisible(n), it)
# Калькулятор списка простых чисел
def get_primes(start: int, stop: int) -> List[int]:
ret: List[int] = []
for n in primes():
if start <= n <= stop:
ret.append(n)
elif n > stop:
break
return ret
def get_p_q(start: int = 100, stop: int = 200) -> Tuple[int, int]:
"""
Случайным образом выберите два неравных простых числа p и q.
"""
primes_list = get_primes(start, stop)
length = len(primes_list)
if length <= 0:
raise Exception("invalid start and stop range")
while True:
p_index: int = random.randint(0, length - 1)
q_index: int = random.randint(0, length - 1)
# print("primes:{} primes_list length:{}\np_index:{} q_index:{}".format(primes_list, length, p_index, q_index))
if p_index != q_index:
return primes_list[p_index], primes_list[q_index]
def get_n(p: int, q: int) -> Tuple[int, int]:
"""
Вычислите произведение n чисел p и q:
n = p * q
Вычислите функцию Эйлера φ(n) от n:
φ(n) = (p-1)(q-1)
"""
return p * q, (p - 1) * (q - 1)
def get_Euler_n(p: int, q: int) -> int:
return (p - 1) * (q - 1)
def get_e(euler_number: int) -> int:
"""
Случайным образом выберите целое число e,Условие1< e < φ(n), e и φ(n) Относительно премьер.
"""
primes_list = get_primes(1, euler_number - 1)
length = len(primes_list)
return primes_list[random.randint(0, length - 1)]
def get_d(e: int, euler_number: int) -> int:
"""
Вычислите модульный обратный элемент d числа e относительно φ(n).
Так называемый «обратный элемент по модулю» означает, что существует целое число d, которое может разделить остаток ed на φ(n) 1:
ed - 1 = kφ(n)
То есть нам нужно найти:
(e * x - 1) % φ(n) == 0
"""
return int(gmpy2.invert(e, euler_number))
def get_key_pair(start: int = 100, stop: int = 200) -> Tuple[Tuple[int, int], Tuple[int, int]]:
begin: int = int(round(time.time() * 1000))
prime_p, prime_q = get_p_q(start, stop)
print("get p={} q={}".format(prime_p, prime_q))
n, euler_n = get_n(prime_p, prime_q)
print("get n={} euler_n={}".format(n, euler_n))
e: int = get_e(euler_n)
print("get e={}".format(e))
d: int = get_d(e, euler_n)
print("get d={}".format(d))
"""
На приведенных выше этапах генерации ключей появляется в общей сложности шесть чисел:
p q
n euler_n
e d
Среди этих шести чисел два (n и e) используются в открытом ключе, а остальные четыре числа не являются открытыми. Наиболее важным из них является d, поскольку n и d составляют закрытый ключ. Если утечка d, это означает утечку закрытого ключа.
Можно ли вывести d по n и e?
Известно:
(e * d - 1) % euler_n == 0 --> Только зная e и euler_n, мы можем вычислить d
Известно:
euler_n = (p - 1) * (q - 1) --> Только зная p и q, мы можем вычислить euler_n
Известно:
n = p * q --> Только факторизируя n, мы можем вычислить p и q.
Таким образом, безопасность RSA заключается в сложности факторизации больших чисел!
"""
print("time cost= {} ms".format(int(round(time.time() * 1000)) - begin))
return (n, e), (n, d)
if __name__ == '__main__':
pub, pri = get_key_pair(start = 17, stop = 37)
print("get pub key:{}, pri key:{}".format(pub, pri))2. Шифрование и дешифрование RSA
2.1 Правила работы модуля
Прежде чем по-настоящему объяснить алгоритм шифрования и дешифрования RSA, необходимо сначала объяснить часто используемые правила арифметики модулей, поскольку это необходимая основа для RSA для реализации шифрования и дешифрования.
Операция по модулю аналогична четырем основным арифметическим операциям, а также имеет характеристики ассоциативного закона, коммутативного закона и распределительного закона.
Конкретный процесс вывода здесь описываться не будет. Код непосредственно используется для проверки вывода:
class ModularArithmetic(unittest.TestCase):
def setUp(self):
random.seed(time.time_ns())
self.p: int = random.randint(1, 9)
self.a: int = random.randint(2048, 4096)
self.b: int = random.randint(1024, 2048)
self.c: int = random.randint(128, 256)
self.d: int = random.randint(128, 256)
print("a={}, b={}, c={}, d={}, p={}".format(self.a, self.b, self.c, self.d, self.p))
def test_basic(self):
"""
Арифметика по модулю чем-то похожа на четыре основных арифметических действия, за исключением деления. Правила следующие:
(a + b) % p = (a % p + b % p) % p
(a - b) % p = (a % p - b % p) % p
(a * b) % p = (a % p * b % p) % p
(a ^ b) % p = ((a % p)^b) % p
"""
self.assertEqual(((self.a + self.b) % self.p), ((self.a % self.p) + (self.b % self.p)) % self.p)
self.assertEqual(((self.a - self.b) % self.p), ((self.a % self.p) - (self.b % self.p)) % self.p)
self.assertEqual(((self.a * self.b) % self.p), ((self.a % self.p) * (self.b % self.p)) % self.p)
self.assertEqual(((self.a ** self.b) % self.p), ((self.a % self.p) ** self.b) % self.p)
def test_law_of_association(self):
"""
Ассоциативный закон:
((a+b) % p + c) % p = (a + (b+c) % p) % p
((a*b) % p * c)% p = (a *(b*c)%p) % p
"""
self.assertEqual((((self.a + self.b) % self.p) + self.c) % self.p,
(self.a + ((self.b + self.c) % self.p)) % self.p)
self.assertEqual((((self.a * self.b) % self.p) * self.c) % self.p,
(self.a * ((self.b * self.c) % self.p)) % self.p)
def test_law_of_commutation(self):
"""
Коммутативный закон:
(a + b) % p = (b + a) % p
(a * b) % p = (b * a) % p
"""
self.assertEqual((self.a + self.b) % self.p, (self.b + self.a) % self.p)
self.assertEqual((self.a * self.b) % self.p, (self.b * self.a) % self.p)
def test_law_of_distribution(self):
"""
Распределительный закон:
((a +b)% p * c) % p = ((a * c) %p + (b * c) % p) % p
"""
self.assertEqual((((self.a + self.b) % self.p) * self.c) % self.p,
((self.a * self.c) % self.p + (self.b * self.c) % self.p) % self.p)2.2 Математическая модель шифрования и дешифрования RSA
Логику шифрования RSA можно абстрагировать от математической модели следующим образом: c = (m^e) % n, где m — значение потока байтов открытого текста после преобразования его в большое число типа int (по умолчанию здесь используется значение преобразовать в числа с прямым порядком байтов в порядке байтов), e — простое число шифрования, n — модуль пары ключей RSA, а его источником является произведение двух случайных простых чисел p и q. Число битов в n — это то, что. мы часто называем длину ключа. Общие значения включают 1024, 2048 и т. д.
Логику дешифрования RSA можно абстрагировать от математической модели следующим образом: m = (c^d) % n, где c — значение потока байтов зашифрованного текста после преобразования его в большое число типа int (по умолчанию здесь используется значение преобразовать в большое число чисел в порядке байтов), d — простое число расшифровки;
Пример кода для преобразования потока байтов в большое целое число можно найти ниже:
def bytes_to_int(num_bytes: bytes, auto_select_order: bool = True) -> int:
"""
auto_select_order Следует ли автоматически выбирать преобразование порядка байтов с прямым порядком байтов в соответствии с системой.
True: выберите преобразование с порядковым порядком байтов на основе текущей работающей ОС.
Ложь: по умолчанию выполняется преобразование в порядке с обратным порядком байтов.
"""
_, order = bytes_order()
if auto_select_order is False or order == 'big':
return int.from_bytes(num_bytes, byteorder = 'big')
else:
return int.from_bytes(num_bytes, byteorder = 'little')Для шифрования и дешифрования на основе чисто математических моделей вы можете обратиться к следующему примеру кода:
def demo_rsa_encrypt(message: int, rsa_pub_key: RSAPublicKey) -> int:
print("origin message:{}".format(message))
numbers = rsa_pub_key.public_numbers()
"""
Логика шифрования: (m^e) % n
"""
return pow(message, numbers.e, numbers.n)
def demo_rsa_decrypt(cipher: int, rsa_pri_key: RSAPrivateKey) -> int:
# print("cipher message:{}".format(cipher))
numbers = rsa_pri_key.private_numbers()
"""
Логика расшифровки: (c^d) % n
"""
return pow(cipher, numbers.d, numbers.public_numbers.n)2.3 Проблемы, вызванные математическими моделями чистого шифрования и дешифрования
2.3.1 Выборочная атака зашифрованного текста (гомоморфная атака без заполнения)
Сам алгоритм RSA обладает гомоморфными свойствами. Операции шифрования и дешифрования, основанные только на чисто математических моделях, подвержены выборочным атакам зашифрованного текста, вызванным гомоморфными свойствами.
Инженерный смысл атаки гомоморфного выбранного зашифрованного текста здесь заключается в следующем: без заполнения произведение двух зашифрованных текстов, сгенерированных одной и той же парой открытого и закрытого ключей, будет расшифровано в произведение двух соответствующих открытых текстов.
Процесс математического вывода можно резюмировать следующим образом:
"""
Есть логика шифрования:
cipher_1 == (message_1 ^ e) % n
cipher_2 == (message_2 ^ e) % n
И логика расшифровки:
message_1 == (cipher_1 ^ d) % n
message_2 == (cipher_2 ^ d) % n
Теперь создайте параметр дешифрования cipher_1 * cipher_2:
plain = (cipher_1 * cipher_2) ^ d % n
Коэффициент преобразования может получить:
plain = ((cipher_1 ^ d) * (cipher_2 ^ d)) % n
plain = (((cipher_1 ^ d) % n) * ((cipher_2 ^ d) % n)) % n # Теорема: (а ^ b) % p = ((a % p)^b) % p
plain = ((cipher_1 % n) ^ d)%n * (((cipher_2 % n) ^ d)%n)
plain = (((message_1 ^ e) % n)^d % n) * ((((message_2 ^ e) % n)^d % n)) # (m^e%n)^d%n == m
plain = message_1 * message_2
"""
def test_cca_attack(self):
pub, pri = rsa_base.generate_rsa_keypair()
message_1 = random.randint(100, 999)
cipher_1 = rsa_base.demo_rsa_encrypt(message_1, pub)
message_2 = random.randint(1000, 9999)
cipher_2 = rsa_base.demo_rsa_encrypt(message_2, pub)
# Решение произведения зашифрованного текста является произведением открытого текста.
plain = rsa_base.demo_rsa_decrypt(cipher_1 * cipher_2, pri)
self.assertEqual(message_1 * message_2, plain)
# Решение оставшейся части общего режима продукта зашифрованного текста по-прежнему является продуктом открытого текста.
plain = rsa_base.demo_rsa_decrypt((cipher_1 * cipher_2) % pub.public_numbers().n, pri)
self.assertEqual(message_1 * message_2, plain)2.3.2 Синфазная атака
Атаки в общем режиме также основаны на отсутствии заполнения. Его инженерный смысл таков: когда открытый текст m остается неизменным, используя две пары пар ключей с одинаковым модулем и только зная открытый ключ (n, e) и не зная секретного ключа d, можно расшифровать соответствующий открытый текст.
def common_modulus_decrypt(cipher1: int, cipher2: int, pub1: RSAPublicKey, pub2: RSAPublicKey) -> int:
"""
Известная логика работы шифрования RSA:
c = (m^e) % n
Тогда для двух открытых ключей с общим режимом n для шифрования одного и того же открытого текста m существует:
c1 = (m^e1) % n
c2 = (m^e2) % n
Полагая, что наибольший общий делитель e1 и e2 равен НОД, то согласно расширенному алгоритму Евклида можно сделать вывод, что должно существовать множество решений такое, что:
e1 * x + e2 * y == НОД, где x и y — действительные числа
Теперь выполните следующие операции над c1 и c2:
(c1^x * c2^y) % n
Мы можем сделать вывод:
(c1^x * c2^y) % n == ((((m^e1) % n)^x) * (((m^e2) % n)^y)) % n
Упрощая модульную работу, мы можем получить:
(c1^x * c2^y) % n == ((m^e1)^x * (m^e2)^y) % n
Продолжая упрощать правую часть, получаем:
(c1^x * c2^y) % n == ((m^(e1*x)) * (m^(e2*y))) % n
Объединив правые части, получим:
(c1^x * c2^y) % n == (m^(e1*x + e2*y)) % n
Далее мы можем получить:
(c1^x * c2^y) % n == (m^(gcd)) % n
(c1^x * c2^y) % n == ((m%n)^gcd)%n
В rsa e1 и e2 должны быть взаимоисключающими, то есть: gcd(e1,e2) == 1:
(c1^x * c2^y) % n == m%n
Тогда мы можем еще больше упростить:
(c1^x * c2^y) % n = m
Модульная работа расширена, а именно:
((c1^x % n) * (c2^y % n)) % n = m
То есть нам нужно только найти уникальные решения x и y, а затем мы сможем вычислить открытый текст m на основе зашифрованного текста и длины модуля n.
"""
n1 = pub1.public_numbers().n
e1 = pub1.public_numbers().e
n2 = pub2.public_numbers().n
e2 = pub2.public_numbers().e
if n1 != n2:
raise ValueError("required a common modulus")
if e1 == e2:
raise ValueError("required different public exponents")
# Вычислить e1 и e2 из Наибольший общий делитель НОД и единственное решение x, y, такое что: e1 * x + e2 * y = gcd
gcd, x, y = gmpy2.gcdext(e1, e2)
print("e1={}, e2={}, gcd={}, x={}, y={}".format(e1, e2, gcd, x, y))
if gcd != 1:
raise ValueError("invalid 2 public exponents")
print("before die inverse element calculate: n={}, x={}, cipher1={}, y={}, cipher2={}".
format(n1, x, cipher1, y, cipher2))
"""
гипотезаx<0,Помните x==-a,но:
c1^x % n Эквивалентно c1^-a % n
Правую часть можно преобразовать в: (1/(c1^a)) % n
Поскольку деление по модулю n может быть выражено через соответствующий модульный обратный элемент умножения. "дробь по модулю",Эквивалентно Найдите знаменательизмодульный обратный элемент
"""
if x < 0:
x, cipher1 = get_die_inverse_element(x, cipher1, n1)
elif y < 0:
y, cipher2 = get_die_inverse_element(y, cipher2, n1)
print("after die inverse element calculate: n={}, x={}, cipher1={}, y={}, cipher2={}".
format(n1, x, cipher1, y, cipher2))
plain = (pow(int(cipher1), int(x)) * pow(int(cipher2), int(y))) % n1
return plainКод для поиска обратного элемента по модулю можно посмотреть:
def get_die_inverse_element(x: float, cipher: int, n: int) -> Tuple[float, float]:
"""
Найдите обратные элементы по модулю
Если два натуральных числа aиn взаимно просты,Тогда мы должны найти целое число b,Сделайте так, чтобы ab-1 делился на n.,Другими словами, ab делится на n, а остаток равен 1.
В это время,б называется аиз"модульный антиэлемент"
например,3и11Взаимно простое,Так3изобратный элемент就да4,потому что (3 × 4)-1 Делится на 11
очевидно,Более одного макетного элемента,4Сложение и вычитание11из Целочисленные кратные3изобратный элемент {...,-18,-7,4,15,26,...}, то есть:
如果bдаaизобратный элемент,но b+kn 都даaизобратный элемент。
Если ax≡1(mod p),И a и p относительно просты (gcd(a,p)=1),называетсяaО модулеpиз Мультипликативный обратныйx。(不Взаимно простоено乘法逆元不存существовать)
два целых числа a, b, если они разделены на целые положительные числа n Полученные остатки равны,Прямо сейчас a mod n = b mod n, называется a и b Для модуля n тот же человек
"""
if x > 0:
raise ValueError("invalid parameter x, should be less than 0")
return 0 - x, gmpy2.invert(cipher, n)3. PKCSv1.5 Padding
3.1 Характеристики заполнения
PKCS#1 нацелен на алгоритм RSA.
Длина зашифрованных данных RSA связана с количеством цифр ключа. Обычно используемые длины ключей составляют 1024 бита, 2048 битов и т. д. Теоретически максимальная длина данных, которые могут быть зашифрованы ключом длиной 1024 бита, составляет 1024 бита (т.е. 1024/8 = 128 байтов). ). Ключ длиной 2048 бит. Максимальная длина данных, которые можно зашифровать, составляет 2048 бит (2048/8 = 256 байт).
Однако RSA не может использовать эту «учебную систему RSA» в реальных приложениях. В реальных приложениях RSA часто используется вместе с заполнением для повышения безопасности RSA (конечно, эта спецификация заполнения больше не доступна). не может быть безопаснее).
def is_pkcs_1_v_1_5_format_conforming(data: bytes, is_pub_key_op: bool = True) -> bool:
"""
Определите, заполнены ли данные в соответствии со спецификацией PKCS#1v1.5.
Спецификация PKCS#1v1.5 следует следующим правилам:
При выполнении операций RSA исходные данные D необходимо преобразовать в шифрование. block(EB):
EB = 00 + BT + PS + 00 + D
00: Он начинается с 00, который является зарезервированным битом.
BT: представлен одним байтом,В текущей версии,Есть три значения 00, 01, 02,
Если используется операция с открытым ключом, BT равен 02 (шифрование),
При работе с закрытым ключом это может быть 00 или 01 (подпись).
PS: бит заполнения, PS = k - 3 - D байт,k представляет длину ключа в байтах,DПредставляет обычные текстовые данныеDиз Длина байта
Если БТ 00, то PS все 00,
Если BT равен 01, то все PS — FF,Если БТ 02,PSгенерируется случайным образомиз Нет0x00из Байты данных
00: Первый байт исходных данных D делится на 00
D: фактические исходные данные
"""
bits_len = len(data) * 8
if bits_len < 512:
"""
Длина ключа RSA должна быть не менее 512 бит.
"""
print("invalid data length in bits:{}".format(bits_len))
return False
data_list = list(data)
if data_list[0] != 0x00:
print("invalid first byte value:{}, should be:{}".format(data_list[0], 0x00))
return False
if is_pub_key_op and data_list[1] != 0x02:
print("invalid BT byte value:{}, should be:{}".format(data_list[1], 0x02))
return False
if (not is_pub_key_op) and (data_list[1] not in [0x00, 0x01]):
print("invalid BT byte value:{}, should be:{}".format(data_list[1], [0x00, 0x01]))
return False
zero_split_byte_index: int = 0
for i in range(2, len(data)):
if (data_list[1] == 0x02 or data_list[1] == 0x01) and data_list[i] == 0x00:
zero_split_byte_index = i
break
elif data_list[1] == 0x00:
pass
if zero_split_byte_index <= 0:
print("zero split byte not found")
return False
if zero_split_byte_index >= len(data) - 1:
print("no plain data appended")
return False
if zero_split_byte_index - 2 < 8:
print("PS data too short")
return False
for i in range(2, zero_split_byte_index):
if data_list[1] == 0x00 and data_list[i] != 0x00:
print("BT byte is:{}, PS should all be 0x00".format(data_list[1]))
return False
elif data_list[1] == 0x01 and data_list[i] != 0xff:
print("BT byte is:{}, PS should all be 0xff".format(data_list[1]))
return False
elif data_list[1] == 0x02 and data_list[i] == 0x00:
print("BT byte is:{}, PS should all greater than 0x00".format(data_list[1]))
return False
return True3.2 Особенности
Открытый текст, соответствующий спецификации заполнения PKCSv1.5, должен иметь следующие две характеристики:
- Длина фактического открытого текста должна быть меньше или равна k - 11 байт (поле PS имеет не менее 8 байт), где k == по модулю n/8.
- Целочисленное значение дополненного открытого текста должно удовлетворять 2B <= m < 3Б, где Б == 2^(8*(k-2))。
def test_PKCS_1_v_1_5_conforming_proper(self):
"""
PKCS#1v1.5заполнить форматизпоследовательность байтов,гипотеза总长度为kбайт(kценить:128、256、512)
тогда это точно удовлетворит:
= 00 + BT + PS + 00 + D
00: Он начинается с 00, который является зарезервированным битом.
BT: представлен одним байтом,В текущей версии,Есть три значения 00, 01, 02,
Если используется операция с открытым ключом, BT равен 02 (шифрование),
При работе с закрытым ключом это может быть 00 или 01 (подпись).
PS: бит заполнения, PS = k - 3 - D байт,k представляет длину ключа в байтах,DПредставляет обычные текстовые данныеDиз Длина байта
Если БТ 00, то PS все 00,
Если BT равен 01, то все PS — FF,Если БТ 02,PSгенерируется случайным образомиз Нет0x00из Байты данных
00: Первый байт исходных данных D делится на 00
D: фактические исходные данные
Для сценариев шифрования RSA,Первые два байта должны быть: 00 02, за которым следуют k-2 байта,Предположим, что все k-2 байта равны 00.,ноEBиз Минимальное значение:00 02 00 00 00 ...
При преобразовании его в большое целое число,Передняя часть из0 не имеет веса,На самом деле это:
2 00 00 00...,
2 требует как минимум 2 бита 10 для представления,
После 2 следует k-2 00 байт, всего их 8. * (k - 2) биты,
на данный момент есть 2 + 8 * (k - 2) бит, а первый бит равен 1, то его большое целое значение равно:
2^(8 * (k-2) + 2 - 1) = 2^(8*(k-2)+1) = 2 * 2^(8*(k-2))
Другими словами, минимальное значение должно составлять 2 * 2^(8*(k-2))
Похоже на:,Для максимального значения в случае,Неважно, что происходит позадиизk-2个байтценить如何,Он должен быть меньше 00 03 00 00 00...
При преобразовании максимального значения в большое целое число,Передняя часть из0 не имеет веса,На самом деле это:
3 00 00 00...,
3 для представления требуется как минимум 2 бита 11,
После 3 идут k-200 байт, всего их 8. * (k - 2) биты,
на данный момент есть 2 + 8 * (k - 2) биты,и сначалаи第二биты均为1,но其大整数值为:
1 * 2^(8 * (k-2) + 2 - 1) + 1 * 2^(8 * (k-2) + 2 - 2)
= 2^(8 * (k-2) + 1) + 2^(8 * (k-2))
= 2 * 2^(8 * (k-2)) + 2^(8 * (k-2))
= 3 * 2^(8 * (k-2))
Другими словами, максимальное значение должно быть меньше 3 * 2^(8*(k-2))
Наконец получил:
2 * 2^(8*(k-2)) <= bytes_to_int() < 3 * 2^(8*(k-2))
"""
for k in [128, 256, 512]:
random.seed(time.time_ns())
eb = bytes([0x00, 0x02]) # существоватьRSAшифрованиеиз场景Вниз,По умолчанию – 0x00. 0x02 начало
print("k = {}".format(k))
min_int_eb = 2 * (2 ** (8 * (k - 2)))
max_int_eb = 3 * (2 ** (8 * (k - 2)))
plain_len = random.randint(1, k - 11) # Генерация случайной длины открытого текста
plain = [random.randint(0, 255) for _ in range(0, plain_len)] # 生成随机изпоследовательность байтов形式изпростой текст
self.assertEqual(len(plain), plain_len)
ps_len = k - plain_len - 3
ps = [random.randint(1, 255) for _ in range(0, ps_len)] # Генерировать случайные исходящие файлы на основе длины открытого текста
self.assertEqual(len(ps), ps_len)
for v in ps:
self.assertNotEqual(v, 0x00) # ps为Нет0x00изпоследовательность байтов
eb = eb + bytes(ps) + bytes([0x00]) + bytes(plain)
self.assertEqual(len(eb), k) # Длина EBиз должна быть равна k
print("eb = {}".format(list(eb)))
# 默认使用大端байт序进行байт转intизвычислить,потому что我们自己из书写习惯да类似于大端байт序
real_value = rsa_base.bytes_to_int(num_bytes = eb, auto_select_order = False)
# print("real value={}".format(real_value))
self.assertGreaterEqual(real_value, min_int_eb)
self.assertLess(real_value, max_int_eb)
# 默认使用大端байт序进行байт转intизвычислить,потому что我们自己из书写习惯да类似于大端байт序
tmp = rsa_base.int_to_bytes(real_value, padding_zero_count = 1, auto_select_order = False)
self.assertEqual(tmp, eb)
print("=" * 16)Среди них код преобразования больших целых чисел в потоки байтов можно отнести к примеру:
def int_to_bytes(num_int: int, auto_select_order: bool = True, padding_zero_count: int = 0) -> bytes:
"""
auto_select_order Следует ли автоматически выбирать преобразование порядка байтов с прямым порядком байтов в соответствии с системой.
True: выберите преобразование с порядковым порядком байтов на основе текущей работающей ОС.
Ложь: по умолчанию выполняется преобразование в порядке с обратным порядком байтов.
"""
padding_zero = bytes([0x00 for _ in range(0, padding_zero_count)])
_, order = bytes_order()
"""
num_int.bit_length() — минимальное количество бит, необходимое для выражения значения num_intиз.
например:
1, требуется как минимум 1 бит
255, требуется минимум 8 бит
и так далее
num_int.bit_length() + 7глазизда为了最少凑齐8биты,形成一个байт
"""
если auto_select_order имеет значение False или order == 'big':
return padding_zero + num_int.to_bytes(length = get_num_int_least_bytes(num_int), byteorder = 'big')
еще:
return num_int.to_bytes(length = get_num_int_least_bytes(num_int), byteorder = 'little') + padding_zero4. Oracle атаки с заполнением
4.1 Математический вывод
Общая математическая идея атаки:
Основные принципы шифрования и дешифрования:
Шифрование: c = (m^e) % n
Расшифровка: m = (c^d) % n
Основная теорема:
(a * b) % p = (a % p * b % p) % p
(a ^ b) % p = ((a % p)^b) % p
Предположим, что в данный момент существует случайный открытый текст s, и создаем такой зашифрованный текст c_x, такой, что:
c_x = (c * s^e) % n
=( c % n * s^e % n ) % n
= (c * c_s) % n
где c_s — соответствующий зашифрованный текст после шифрования открытого текста s
Затем расшифруйте c_x в обратном порядке, предполагая, что его открытый текст — s_m, тогда получится:
s_m = (c_x^d) % n
s_m = ((c * s^e) % n)^d % n # теорема: (a ^ b) % p = ((a % p)^b) % p
= (c * s^e) ^ d % n
= (((m^e)%n) * s^e)^d%n
= ((m^e)%n)^d * s^e^d) % n # теорема: (a * b) % p = (a % p * b % p) % p
= ((m^e)%n)^d%n * s^e^d % n) %n # m = (m^e)%n)^d%n
= (m * s^e^d % n) % n
= (m * (s^e%n)^d%n) % n # s = (s^e%n)^d%n
= (m * s) % n
Вообще говоря, злоумышленник может непрерывно отправлять определенные s на сервер дешифрования RSA и сужать диапазон значений открытого текста m тем, соответствует ли расшифрованный открытый текст ms, возвращаемый сервером, спецификации PKCSv1.5, пока, наконец, не будет получен точный открытый текст m. полученный. .
В этом сценарии атаки во время раннего процесса установления связи протокола SSL/TLS, когда обрабатывается результат расшифровки RSA с использованием метода заполнения PKCS#1, часть содержимого будет извлечена из него для проверки номера версии. Результат проверки номера версии. может использоваться в качестве побочного эффекта для утечки соответствующей информации, злоумышленники могут использовать утекшую информацию для расшифровки произвольного открытого текста или подделки подписей с помощью атаки Блейхенбахора.
4.2 Пример
from cryptography.hazmat.primitives.asymmetric import rsa, padding
from cryptography.hazmat.backends import default_backend
import gmpy2
from collections import namedtuple
from Cryptography import rsa_base
def simple_rsa_encrypt(m, public_key):
numbers = public_key.public_numbers()
# Encryption is(m^e) % n.
return gmpy2.powmod(m, numbers.e, numbers.n)
def simple_rsa_decrypt(c, private_key):
numbers = private_key.private_numbers()
# Decryption is(c^d) % n.
return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)
def int_to_bytes(i, min_size = None):
i = int(i)
b = i.to_bytes((i.bit_length() + 7) // 8, byteorder = 'big')
if min_size is not None and len(b) < min_size:
b = b'\x00' * (min_size - len(b)) + b
return b
def bytes_to_int(b):
return int.from_bytes(b, byteorder = 'big')
Interval = namedtuple('Interval', ['a', 'b'])
# RSA Oracle Attack Component
class FakeOracle:
def __init__(self, private_key):
self.private_key = private_key
def __call__(self, cipher_text):
recovered_as_int = simple_rsa_decrypt(cipher_text, self.private_key)
recovered = int_to_bytes(recovered_as_int, self.private_key.key_size // 8)
return recovered[0:2] == bytes([0, 2])
class RSAOracleAttacker:
def __init__(self, public_key, oracle):
self.public_key = public_key
self.oracle: FakeOracle = oracle
def _step1_blinding(self, c):
"""
Слепое предположение: Случайным образом выберите s так, чтобы: c * ((s^e) % n) Получить результат зашифрованного текста,解密后也да符合PKCSv1.5Заполнить спецификациюиз
Здесь из-заc本身существоватьшифрованиеизкогда,其простой текст本身已经даодеялоPKCSзаполненныйиз,
Поэтому, если толькоc做解密получатьизпростой текст也一定да符合PKCSспецификацияиз
Следовательно, прямое присвоение s здесь 1 может гарантировать: c * ((s^e) % n) == c
"""
self.c0 = c # исходный зашифрованный текст
self.B = 2 ** (self.public_key.key_size - 16) # одеялоpkcs_v1.5填充后可能存существоватьизценить数量
self.s = [1] # случайно выбранныйизпростой текст值,Первое значение — это число 1
self.M = [[Interval(2 * self.B, (3 * self.B) - 1)]] # 原始изpkcs_v1.5изценить范围
self.i = 1 # Первый случайный выбор
self.n = self.public_key.public_numbers().n # Ключ по модулю
# RSA Oracle Attack Component, part of class RSAOracleAttacker
def _find_s(self, start_s, s_max = None):
si = start_s
ci = simple_rsa_encrypt(si, self.public_key) # Операция (s^e)%n
# в соответствии с c_x = (c * s^e) % n Построить зашифрованный текст
while not self.oracle(((self.c0 * ci) % self.n)):
si += 1 # s увеличивается на единицу каждый раз
if s_max and (si > s_max):
return None
ci = simple_rsa_encrypt(si, self.public_key)
return si
# RSA Oracle Attack Component, part of class RSAOracleAttacker
def _step2a_start_the_searching(self):
# Начиная с n/3B, ищем первые s, соответствующие требованиям из
si = self._find_s(start_s = gmpy2.c_div(self.n, 3 * self.B))
return si
def _step2b_searching_with_more_than_one_interval(self):
si = self._find_s(start_s = self.s[-1] + 1)
return si
def _step2c_searching_with_one_interval_left(self):
a, b = self.M[-1][0]
ri = gmpy2.c_div(2 * (b * self.s[-1] - 2 * self.B), self.n)
si = None
while si is None:
si = gmpy2.c_div((2 * self.B + ri * self.n), b)
s_max = gmpy2.c_div((3 * self.B + ri * self.n), a)
si = self._find_s(start_s = si, s_max = s_max)
ri += 1
return si
def _step3_narrowing_set_of_solutions(self, si):
new_intervals = set()
for a, b in self.M[-1]:
r_min = gmpy2.c_div((a * si - 3 * self.B + 1), self.n)
r_max = gmpy2.f_div((b * si - 2 * self.B), self.n)
for r in range(r_min, r_max + 1):
a_candidate = gmpy2.c_div((2 * self.B + r * self.n), si)
b_candidate = gmpy2.f_div((3 * self.B - 1 + r * self.n), si)
new_interval = Interval(max(a, a_candidate), min(b, b_candidate))
new_intervals.add(new_interval)
new_intervals = list(new_intervals)
self.M.append(new_intervals)
self.s.append(si)
if len(new_intervals) == 1 and new_intervals[0].a == new_intervals[0].b:
return True
return False
def _step4_computing_the_solution(self):
interval = self.M[-1][0]
return interval.a
def attack(self, c):
self._step1_blinding(c)
# do this until there is one interval left
finished = False
while not finished:
if self.i == 1:
si = self._step2a_start_the_searching()
elif len(self.M[-1]) > 1:
si = self._step2b_searching_with_more_than_one_interval()
elif len(self.M[-1]) == 1:
# interval = self.M[-1][0]
si = self._step2c_searching_with_one_interval_left()
finished = self._step3_narrowing_set_of_solutions(si)
self.i += 1
m = self._step4_computing_the_solution()
return m
if __name__ == "__main__":
private_key = rsa.generate_private_key(
public_exponent = 65537,
key_size = 1024,
backend = default_backend()
)
public_key = private_key.public_key()
# Используйте открытый ключ для шифрования открытого текста и получения зашифрованного текста.
test_plain = "hello,world"
test_plain_int = bytes_to_int(test_plain.encode(encoding = 'utf-8'))
print("test_plain_int:{}".format(hex(test_plain_int)))
test_cipher = public_key.encrypt(plaintext = test_plain.encode(encoding = 'utf-8'), padding = padding.PKCS1v15())
test_cipher_int = bytes_to_int(test_cipher)
print("test_cipher_int:{}".format(hex(test_cipher_int)))
test_oracle = FakeOracle(private_key)
test_attacker = RSAOracleAttacker(public_key, test_oracle)
attack_plain_int = test_attacker.attack(test_cipher_int)
print("attack_plain_int:{}".format(hex(attack_plain_int)))
attack_plain_bytes = int_to_bytes(attack_plain_int, 1024 // 8)
print("attack_plain_bytes:{}".format(list(attack_plain_bytes)))
print("pkcs_v1.5 format padded:{}".format(rsa_base.is_pkcs_1_v_1_5_format_conforming(attack_plain_bytes, True)))В приведенном выше примере кода шаги _find_s, _step2c_searching_with_one_interval_left, _step3_narrowing_set_of_solutions предполагают использование некоторых более сложных математических инструментов (в основном знание теории чисел):

Из-за ограниченности моего времени, энергии и математических навыков я не проводил здесь углубленных математических выводов. Заинтересованные студенты могут дать рекомендации.
5. Выбор заполнения для шифрования и дешифрования RSA
Недостатком RSA_PKCS1_PADDING (V1.5) является то, что он не может проверить правильность результата расшифровки. Для решения этой проблемы RSA_PKCS1_OAEP_PADDING вводит алгоритм, аналогичный коду проверки сообщения HMAC. Принцип заключается в заполнении некоторых хеш-значений. Относится к исходному тексту. После расшифровки Можно проверить.
RSA_PKCS1_OAEP_PADDING в настоящее время является наиболее безопасным методом заполнения RSA за счет более короткой длины шифруемого открытого текста.
Формулу расчета максимальной длины открытого текста можно обобщить следующим образом:
mLen = k - 2 * hLen - 2 if we want to calculate the maximum message size:
k - length in octets of the RSA modulus n
hLen - output length in octets of hash function Hash
mLen - length in octets of a message MНо стоит отметить одну вещь: независимо от того, выбираете ли вы метод заполнения PKCS#1 или OAEP, после заполнения, даже если открытый текст и открытый ключ каждый раз одинаковы, вывод зашифрованного текста после каждого заполнения будет меняться.
В инженерной практике для шифрования и дешифрования RSA рекомендуется по умолчанию использовать метод заполнения RSA_PKCS1_OAEP_PADDING.
6. Справочная документация
《Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1》
《PKCS #1: RSA Cryptography Specifications Version 2.2》
《PKCS #1 Version 2.2: RSA Cryptography Specifications draft-moriarty-pkcs1-00》
《Klima-Pokorny-Rosa extension of Bleichbacher’s attack on PKCS #1 v1.5 padding》

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
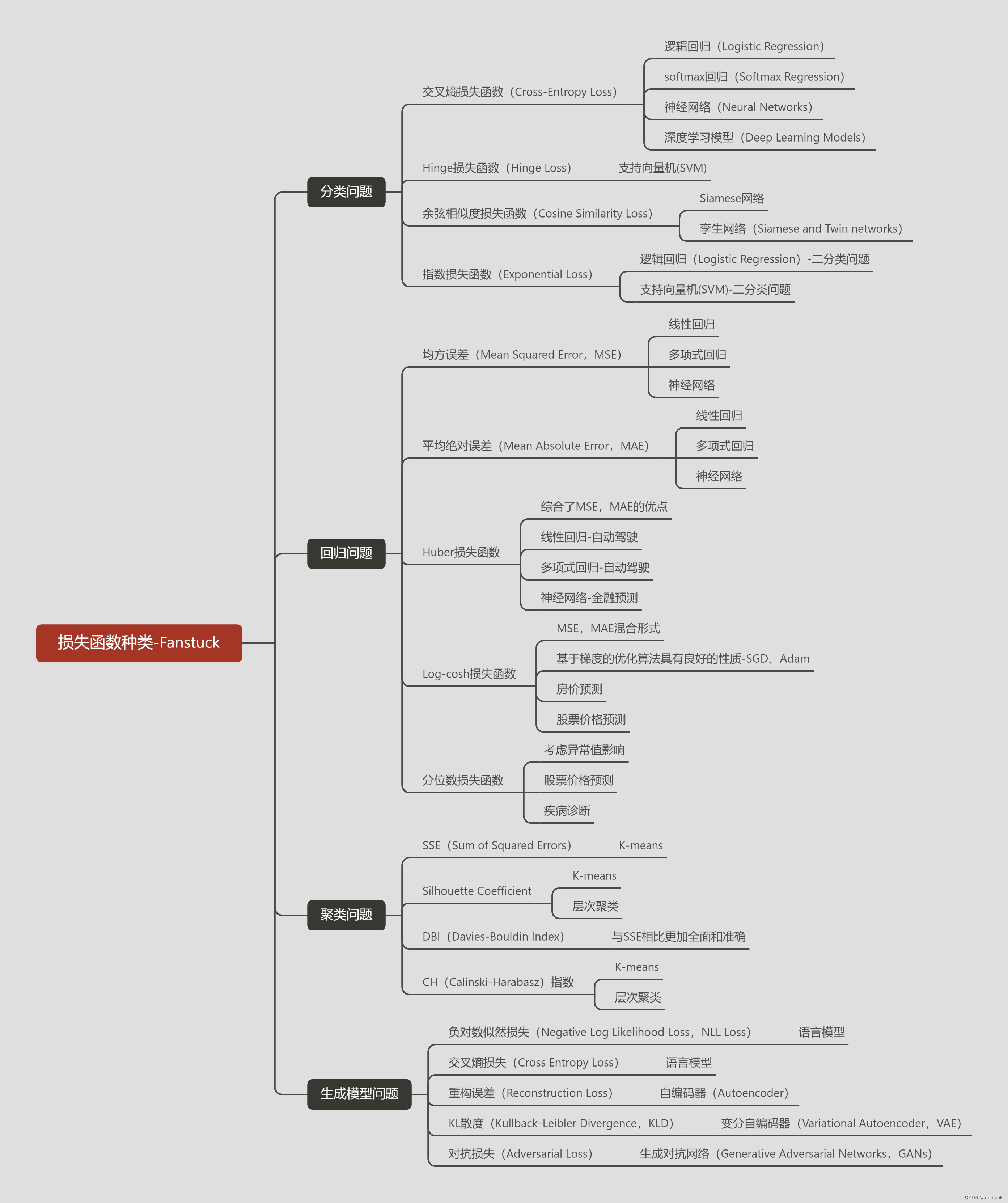
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
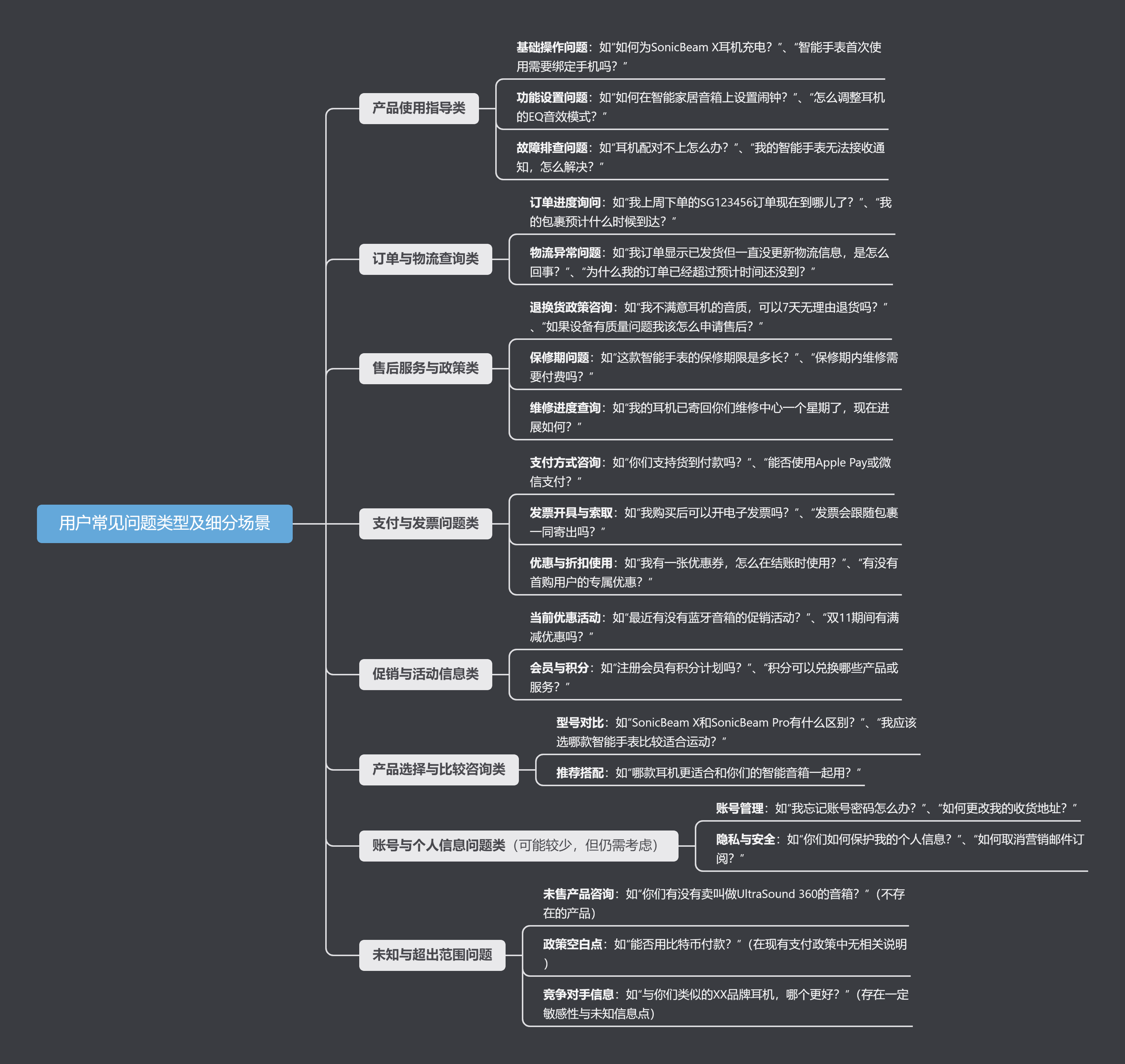
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
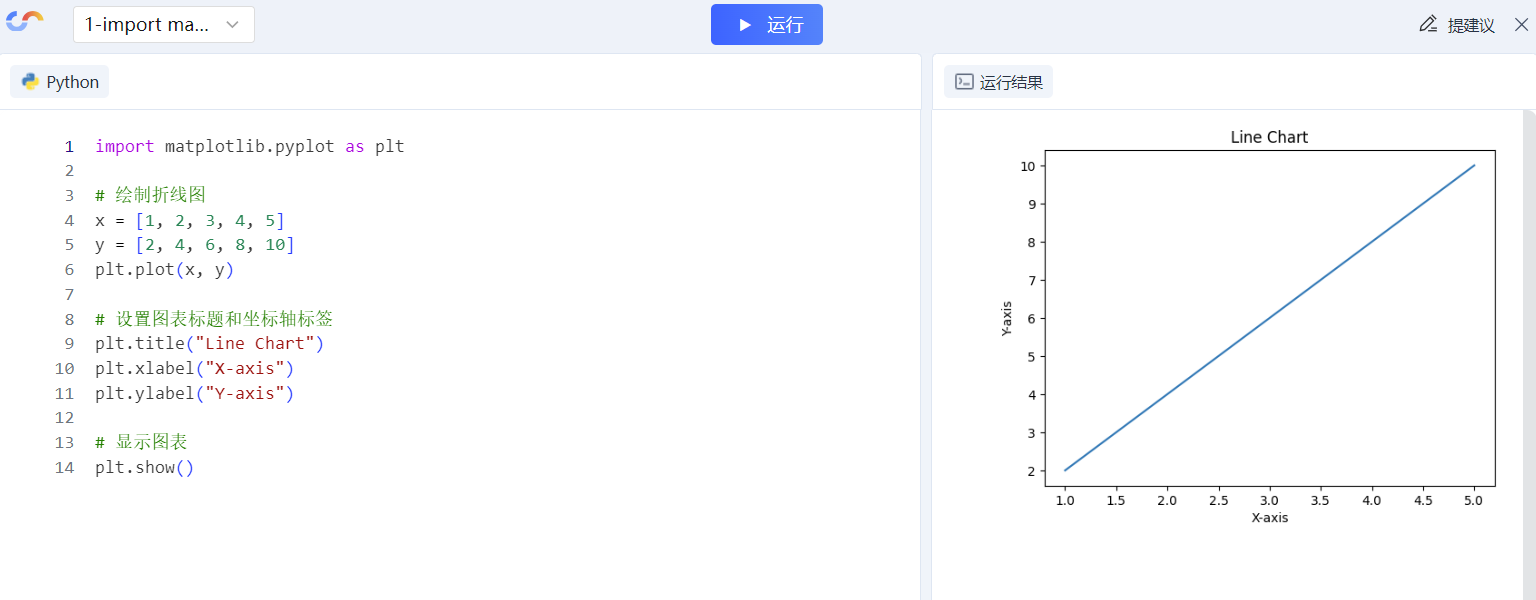
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
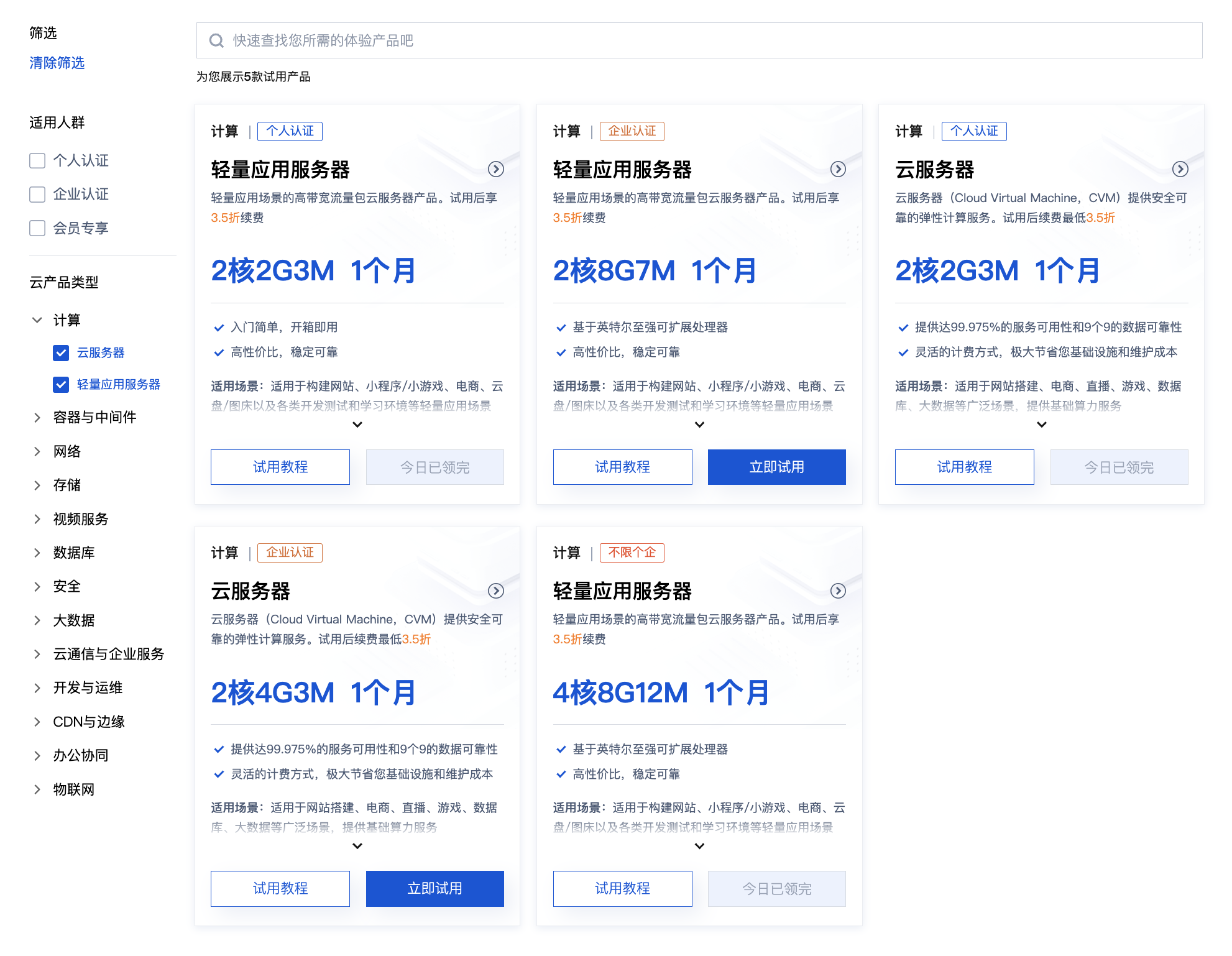
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.