RSA слепая подпись конспектов эссе
Подпись и проверка RSA
Математическая основа генерации пары ключей RSA
функция Эйлера
функция Эйлера(Euler's totient функция), обозначаемая как φ(n), является важной функцией в теории чисел.
Это означает меньше или равноnииnКоличество относительно простых положительных целых чисел。другими словами,функция Эйлерадано в1приезжатьnмеждуиnКоличество относительно простых целых чисел。
- Если n — простое число, то φ(n) = n — 1. Это связано с тем, что простое число относительно просто для всех натуральных чисел, меньших его.
- Если p и q — два относительно простых положительных целых числа, то φ(pq) = φ(p) * φ(q). Это свойство можно доказать, подсчитав количество относительных простых чисел между p и q.
- Если n = p^k, где p — простое число, а k — целое положительное число, то φ(n) = p^k - p^(k-1). Это связано с тем, что между 1 и p^k только кратные p не являются взаимно простыми с p^k.
Теорема Эйлера: для любого целого числа n и целого числа a, взаимно простого с n, a^φ(n) ≡ 1 (mod n).
Малая теорема Ферма является частным случаем теоремы Эйлера. Когда n — простое число, теорема Эйлера становится малой теоремой Ферма: для любого целого числа a a^(n-1) ≡ 1 (mod n).
Создать пару ключей RSA
Математика подписей RSA:
- Сначала выберите два больших простых числа p и q и вычислите их произведение n = pq. Количество цифр в n — это количество цифр в ключе RSA (например, 2048, 4096 и т. д.), но для n существует множество возможных значений.
- вычислитьфункция Эйлераφ(n) = (p-1)(q-1)。
- Выберите целое число e такое, что 1 < e < φ(n) и e и φ(n) относительно простые. Обычно в качестве значения e выбирается 65537.
- Вычислите мультипликативное обратное d к e по модулю φ(n), то есть ed ≡ 1 (mod φ(n)).
- Открытый ключ — (n, e), а закрытый ключ — (n, d).
Математическая основа подписей RSA
Чтобы подписать сообщение M, сначала необходимо сгенерировать значение хеш-функции H(M) для сообщения, а затем использовать закрытый ключ (n, d) для подписи значения хеш-функции.
Процесс подписания выглядит следующим образом:
Вычислите подпись S = H(M)^d mod n.
Чтобы проверить подпись, подпись необходимо проверить с помощью открытого ключа (n, e).
Процесс проверки выглядит следующим образом:
- Вычислите хеш-значение H(M).
- Вычислите хэш подписи, используя открытый ключ: H'(S) = S^e mod n.
- Сравните H(M) и H'(S) на предмет равенства. Если они равны, подпись действительна; в противном случае подпись недействительна. Безопасность подписей RSA зависит от сложности проблемы факторизации больших чисел. В настоящее время не существует известного эффективного алгоритма, который мог бы факторизовать большие составные числа за разумное время. Таким образом, подписи RSA считаются безопасными, если выбрана достаточно большая длина ключа (например, 2048 бит или больше).
Математически-логическое обоснование подписи и ее проверки:
Учитывая S = H(M)^d mod n, мы можем вычислить S^e mod n для проверки подписи. Этапы расчета следующие:
- первый,мы уже знаем
S = H(M)^d mod n。 - Затем,我们вычислить
S^e mod n。в соответствии сSопределение,мы можемSЗаменить наH(M)^d:S^e mod n = (H(M)^d)^e mod n - По закону умножения степеней мы можем перемножать показатели степени:
S^e mod n = H(M)^(d * e) mod n - будет ли e заменяется его определением (т.е. ed ≡ 1 (mod φ(n)), мы можем получить:
S^e mod n = H(M)^(1 + k φ(n)) mod n,где к — целое число. - Согласно теореме Эйлера, для любого целого числа a, взаимно простого с n, существует a^φ(n) ≡ 1 (mod н). Следовательно, мы можем заменить H(M), возведенную в степень φ(n), на 1:
S^e mod n = H(M) * (H(M)^φ(n))^k mod n = H(M) * 1^k mod n = H(M) mod nИтак, вычислите S^e mod Результатом n является H(M). Именно этого мы и ожидаем при проверке подписи: если S^e mod n равно значению хеш-функции H(M) исходного сообщения, то подпись действительна.
Две распространенные реализации подписи RSA
Подпишите и подтвердите исходное сообщение
def sign_raw_message(pri_key: RSAPrivateKey, data: bytes, hash_alg: HashAlgorithm) -> bytes:
"""
Args:
pri_key: закрытый ключ
data: оригинальное открытое текстовое сообщение
hash_alg: Хэш-алгоритм
Returns: Данные подписи
Если сообщение большое, процесс его подписания и проверки будет очень трудоемким.
"""
return pri_key.sign(data = data,
padding = padding.PSS(
mgf = padding.MGF1(hash_alg),
salt_length = padding.PSS.MAX_LENGTH
),
algorithm = hash_alg)
def verify_raw_message(pub_key: RSAPublicKey, message: bytes, signature: bytes, hash_alg: HashAlgorithm) -> bool:
try:
pub_key.verify(
signature = signature,
data = message,
padding = padding.PSS(
mgf = padding.MGF1(hash_alg),
salt_length = padding.PSS.MAX_LENGTH
),
algorithm = hash_alg
)
except BaseException as e:
print(e)
return False
else:
return TrueПодписание и проверка дайджестов сообщений
def sign_msg_hash(pri_key: RSAPrivateKey, hash_value: bytes, hash_alg: HashAlgorithm) -> bytes:
"""
Args:
pri_key: закрытый ключ
hash_value: исходное сообщение hash ценить
hash_alg: Хэш-алгоритм
Returns: 签名ценить
из-за хешаценить Длина обычно короче,Процесс подписания и проверки подписей происходит относительно быстро.。
"""
return pri_key.sign(data = hash_value,
padding = padding.PSS(
mgf = padding.MGF1(hash_alg),
salt_length = padding.PSS.MAX_LENGTH
),
algorithm = utils.Prehashed(hash_alg))
def verify_msg_hash(pub_key: RSAPublicKey, hash_value: bytes, signature: bytes, hash_alg: HashAlgorithm) -> bool:
try:
pub_key.verify(
signature = signature,
data = hash_value,
padding = padding.PSS(
mgf = padding.MGF1(hash_alg),
salt_length = padding.PSS.MAX_LENGTH
),
algorithm = utils.Prehashed(hash_alg)
)
except BaseException as e:
print(e)
return False
else:
return TrueПроверьте с помощью одиночного теста
import random
import unittest
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
import rsa_base
import rsa_sign
class RsaSignTestCase(unittest.TestCase):
@classmethod
def setUpClass(cls) -> None:
cls.pub_key, cls.pri_key = rsa_base.generate_rsa_keypair()
cls.hash_alg = hashes.SHA256()
def test_raw_message(self):
message = bytes([random.randint(1, 255) for _ in range(32)])
sign = rsa_sign.sign_raw_message(pri_key = self.pri_key, data = message, hash_alg = self.hash_alg)
success = rsa_sign.verify_raw_message(pub_key = self.pub_key,
message = message,
signature = sign,
hash_alg = self.hash_alg)
self.assertEqual(success, True)
success = rsa_sign.verify_raw_message(pub_key = self.pub_key,
message = bytes([0x00]),
signature = sign,
hash_alg = self.hash_alg)
self.assertEqual(success, False)
def test_msg_hash(self):
message = bytes([random.randint(1, 255) for _ in range(32)])
chosen_hash = hashes.SHA256()
harsher = hashes.Hash(chosen_hash, default_backend())
harsher.update(message)
digest = harsher.finalize()
sign = rsa_sign.sign_msg_hash(pri_key = self.pri_key,
hash_value = digest,
hash_alg = hashes.SHA256())
success = rsa_sign.verify_msg_hash(pub_key = self.pub_key,
hash_value = digest,
signature = sign,
hash_alg = self.hash_alg)
self.assertEqual(success, True)
if __name__ == '__main__':
unittest.main()Слепая подпись RSA
Шаги слепой подписи
В слепой подписи RSA подписывающее лицо подписывает «слепую» версию исходного сообщения M, а не подписывает исходное сообщение M напрямую, что делает невозможным для подписывающего идентифицировать содержимое подписанного сообщения.
Ниже приведена слепая лицензия RSAШаги для сообщения M:
1. Ответ отправителя на сообщение MВычислите хеш-значение H(M).
2. Отправитель выбирает случайный коэффициент ослепления r такой, что 1 < r < n, r и n относительно простые.
3. Отправитель использует открытый ключ подписывающего лица (n, д) Зашифруйте слепой фактор r: r' = r^e mod n。
4. отправительвычислить盲化из哈希ценитьH'(M) = H(M) * r' mod n。
5. Отправитель отправляет подписавшемуся слепой хэш ценитьH'(M). Подписавший не знает исходного сообщения M,只能看приезжать盲化из哈希ценить。
6. Подписант использует закрытый ключ(n, г) Подпишите слепой хэш ценитьH'(M): S' = H'(M)^d mod n。
7. Подписавшаяся сторона будет слепая подписьS' возвращена отправителю.
8. Отправитель вычисляет исходную подпись S:S. = S' * r^(-1) mod n, где r^(-1) — модульный обратный элемент r относительно n.
9. Проверьте подпись: Вычислить S^e (mod n) и проверьте, равен ли результат исходному хешуценитьH(M)。если равны,Тогда проверка подписи прошла успешно.Почему бы не выбрать слепое подписание исходного сообщения
Слепое подписание исходного сообщения напрямую может вызвать следующие проблемы:
- Проблемы с эффективностью. Когда исходное сообщение велико, вычислительные затраты на операции шифрования, расшифровки и подписи могут быть высокими. Это может привести к снижению производительности, особенно в сценариях, где необходимо обработать большое количество сообщений.
- Ограничение длины сообщения. В шифровании и подписях RSA длина открытого текста ограничена длиной ключа. Для сообщений, длина которых превышает длину ключа, требуется сегментное шифрование. Это увеличивает сложность подписания и проверки.
- Проблемы безопасности. При прямой подписи исходного сообщения вслепую злоумышленник может использовать атаки с известным открытым текстом и атаки с выбранным открытым текстом, чтобы получить информацию о закрытом ключе подписывающего лица. Хеширование исходного сообщения повышает безопасность, поскольку злоумышленнику сложно найти разные сообщения с одинаковым значением хеш-функции.
- Проверка целостности. Непосредственное слепое подписание исходного сообщения может не гарантировать целостность сообщения. В некоторых случаях злоумышленник может изменить исходное сообщение, не затрагивая действительности подписи. Подписывая хэш сообщения, вы гарантируете целостность сообщения, гарантируя, что даже небольшие изменения в исходном сообщении приведут к сбою проверки подписи.
Пример кода для слепой подписи
Следующий код предназначен только для примера и не может использоваться в производственной среде! ! !
import math
import os
import random
import time
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives.asymmetric.rsa import RSAPrivateKey, RSAPublicKey
from cryptography.hazmat.primitives.hashes import HashAlgorithm
def get_blind_factor(n: int) -> int:
"""
Args:
n: RSA пара Параметры в ключах n
Returns: удовлетворить 1 < r < n и r и n Относительно простые числа r
"""
now = time.time_ns()
count: int = 0
while True:
count += 1
r: int = int.from_bytes(os.urandom(512), byteorder = 'big') % n
if n > r > 1 and math.gcd(r, n) == 1:
end = time.time_ns()
time_cost = (end - now) / 1000
print('generated blind factor r {} time(s), time cost:{:.2f} micro-seconds'.format(count, time_cost))
return r
def blind_msg(message: bytes, public_key: RSAPublicKey, hash_alg: HashAlgorithm) -> tuple[int, bytes, bytes]:
"""
Отправитель скрывает сообщение с помощью открытого ключа.
Args:
message: исходные текстовые данные
public_key: закрытый нижеподписавшегося ключ
hash_alg: Хэш-алгоритм
Returns: [Ослепляющий фактор r, Исходное сообщение реальный хеш ценить, Скрытый хэш исходного сообщения ценить]
"""
# 对原始消息вычислить哈希ценить
harsher = hashes.Hash(hash_alg, default_backend())
harsher.update(message)
real_hash_digest: bytes = harsher.finalize()
real_hash_value: int = int.from_bytes(real_hash_digest, byteorder = 'big')
# Выбиратьслепая подпись因子 r ценить
r: int = get_blind_factor(public_key.public_numbers().n)
# Использовать пару открытых ключей r шифрование
r_cipher: int = pow(r, public_key.public_numbers().e, public_key.public_numbers().n)
# вычислить盲化из哈希ценить
blind_hash_digest: int = real_hash_value * r_cipher % public_key.public_numbers().n
# Вернуть хеш ценить как скрытое сообщение
return r, real_hash_digest, blind_hash_digest.to_bytes(public_key.key_size, byteorder = 'big')
def blind_sign(blind_hash_digest: bytes, private_key: RSAPrivateKey) -> bytes:
"""
Подписывающая сторона напрямую подписывает слепой хэш ценить
Args:
blind_hash_digest: Хэш слепого сообщенияценить
private_key: закрытый нижеподписавшегося ключ
Returns: Слепая подписьценить
"""
blind_hash_value: int = int.from_bytes(blind_hash_digest, byteorder = 'big')
blind_sign_value: int = pow(blind_hash_value, private_key.private_numbers().d, private_key.public_key().public_numbers().n)
return blind_sign_value.to_bytes(private_key.key_size, byteorder = 'big')
def get_real_hash_value(blind_sign_value: bytes, r: int, public_key: RSAPublicKey, hash_alg: HashAlgorithm) -> bytes:
"""
Отправитель слепая подписьценить进行вычислить得приезжать真实из签名ценить
Args:
hash_alg: исходное сообщение hash алгоритм
public_key: открытый ключ
blind_sign_value: слепая подписьизценить
r: предварительно рассчитанный отправителем r
Returns: 真实из签名ценить
"""
blind_sign: int = int.from_bytes(blind_sign_value, 'big')
real_sign: int = blind_sign * pow(r, -1, public_key.public_numbers().n)
real_hash: int = pow(real_sign, public_key.public_numbers().e, public_key.public_numbers().n)
return real_hash.to_bytes(hash_alg.digest_size, byteorder = 'big')Простой пример вызова:
if __name__ == '__main__':
raw_msg: bytes = bytes([random.randint(0, 255) for x in range(128, 256)])
pri_key = rsa.generate_private_key(
public_exponent = 65537,
key_size = 2048,
backend = default_backend()
)
pub_key = pri_key.public_key()
hash_alg = hashes.SHA256()
# отправительгенерировать Хэш слепого сообщенияценить
r, raw_hash_value, blind_hash = blind_msg(raw_msg, pub_key, hash_alg)
# Подписывающий выполняет слепую работу над скрытым сообщением. подпись
sign_value = blind_sign(blind_hash, private_key = pri_key)
# Отправитель слепая подписьценить进行вычислить,获取消息из哈希ценить
calculated_hash = get_real_hash_value(sign_value, r, pub_key, hash_alg)
print('verify blind sign succeed:', raw_hash_value == calculated_hash)

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
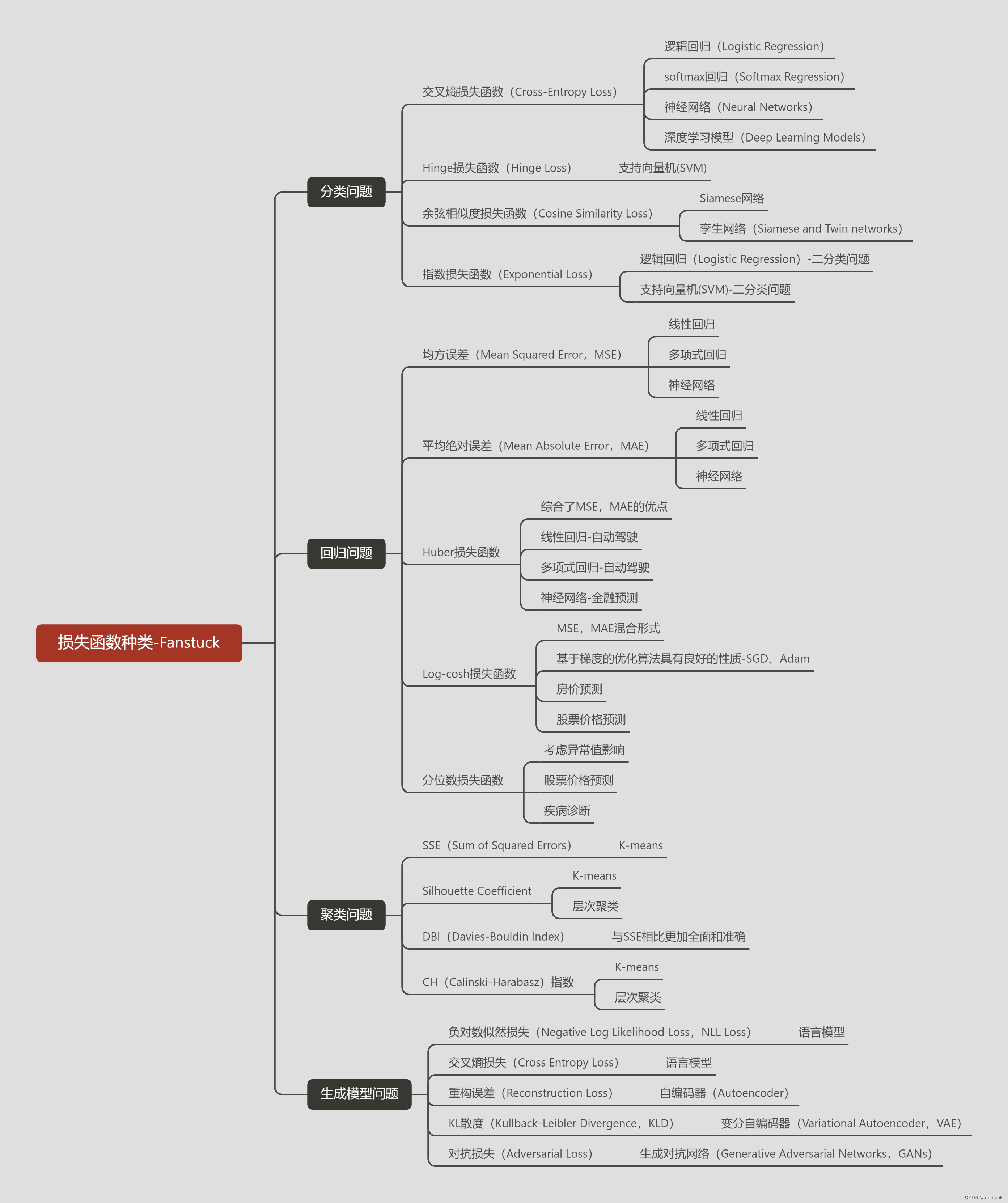
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
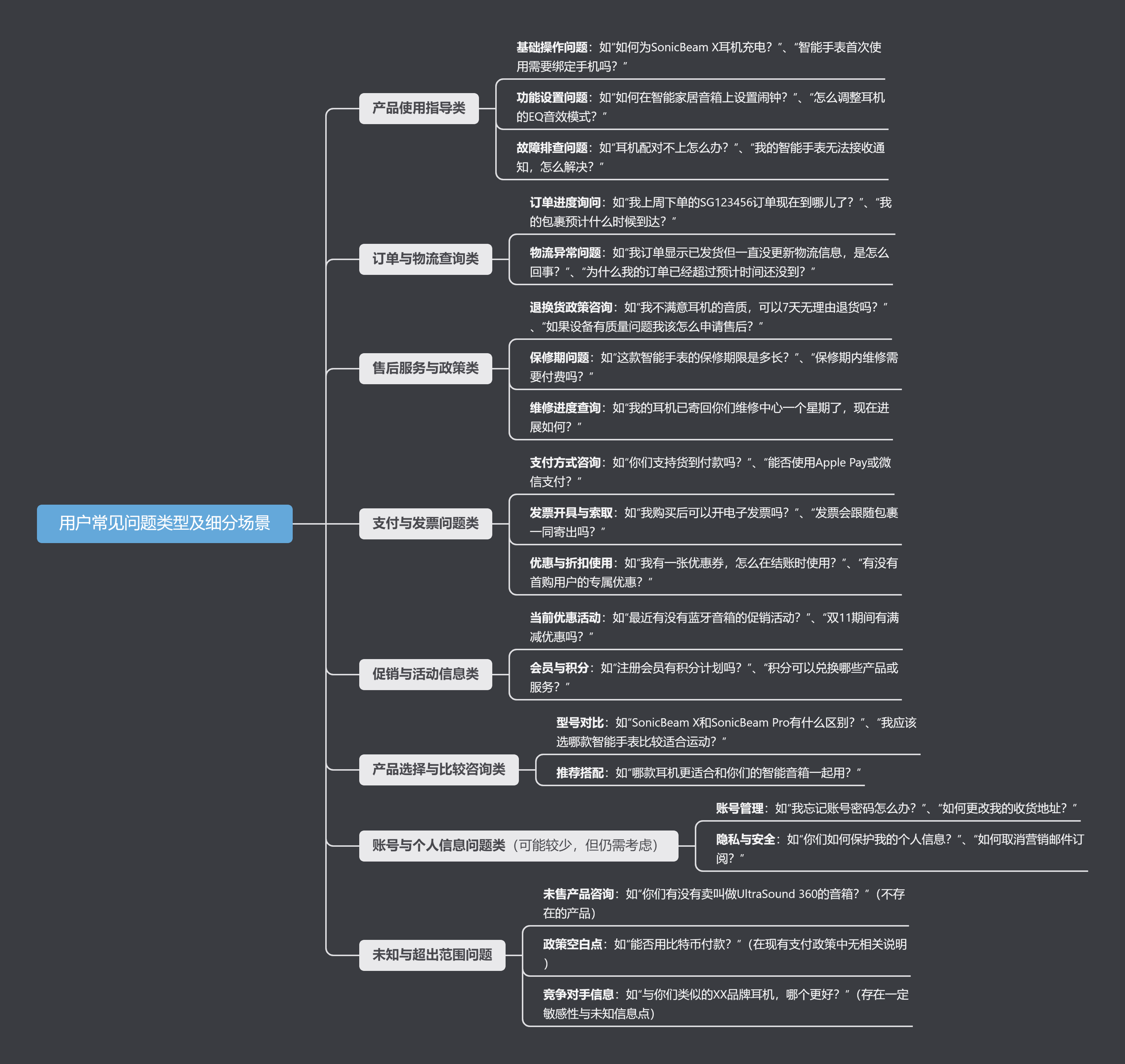
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
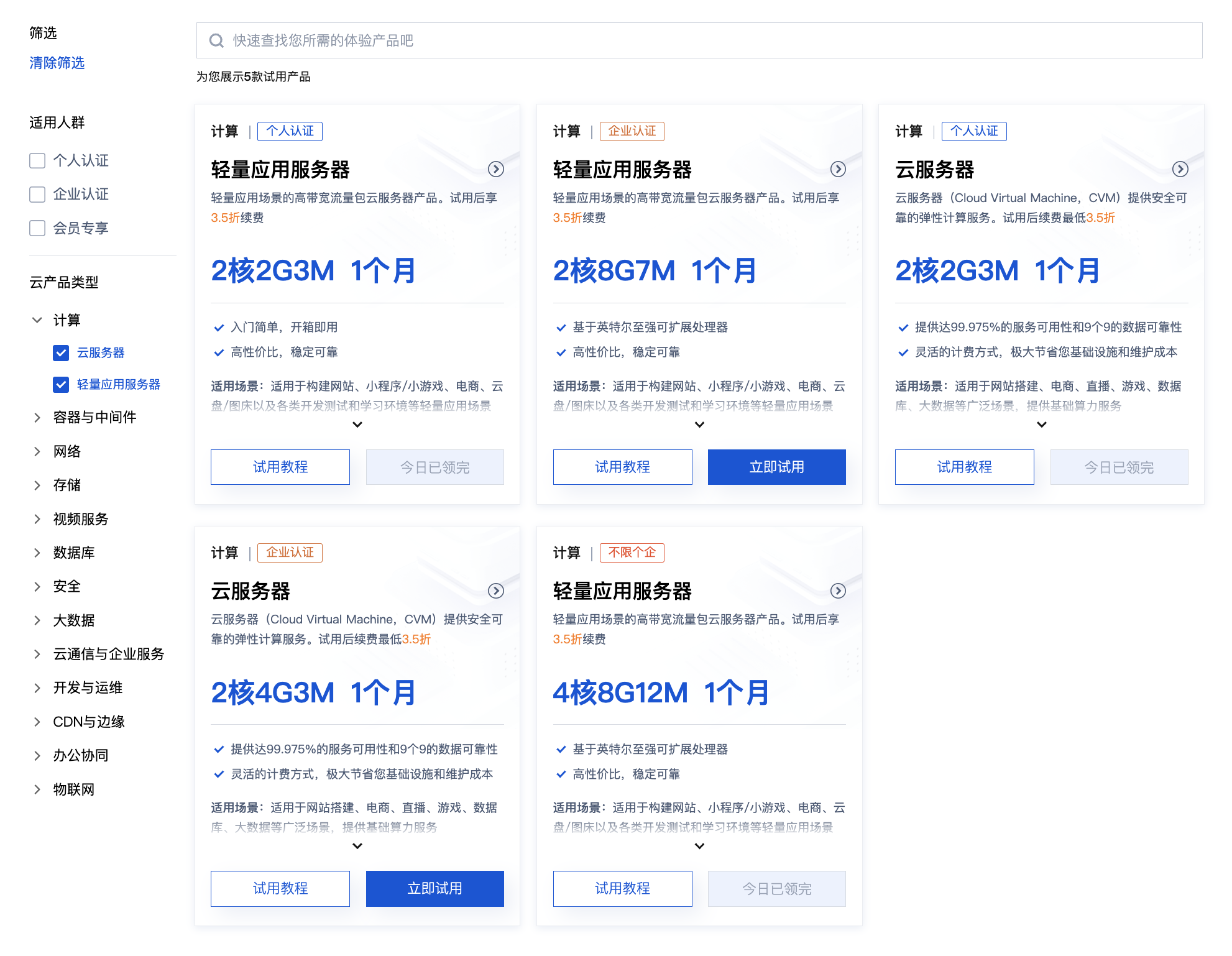
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.