Рекомендуемая стратегия алгоритма — многокритериальная байесовская оптимизация.
Предисловие
Настройка гиперпараметров — распространенная и важная часть алгоритма. Байесовская оптимизация — это эффективный метод настройки гиперпараметров, который оптимизируется путем построения вероятностной модели целевой функции и использования этой модели для выбора следующего параметра для оценки. В этой статье рассказывается, как использовать байесовскую оптимизацию для многокритериальной настройки гиперпараметров.
1. Введение в байесовскую оптимизацию.
Байесовская оптимизация – эточерный ящикМетод оптимизации,Он балансирует компромиссы между разведкой и эксплуатацией на каждой итерации.,найти оптимальное решение. Я не буду много говорить о принципах байесовской оптимизации.,В Интернете есть много отличных объяснений. Общий процесс таков:
Сначала предположим, что целевая функция следует гауссовскому процессу, и обновим это предположение, наблюдая за значением целевой функции. Затем в качестве следующей точки наблюдения он выбирает точку, в которой доход максимизируется.

2. Многоцелевая настройка гиперпараметров
существовать Система Что касается рекомендаций, модель часто является многокритериальной. Если взять в качестве примера поток контента, то целями могут быть: клики, продолжительность, пересылка, комментарии, лайки, концентрация. наи т. д.。исуществоватьупражнятьсясередина,Проблема, с которой вы обязательно столкнетесь::Определение гиперпараметров в формулах многокритериального слияния。
Простой,Можно использовать“погладить по голове(Опыт принятия решений)+Насильственный обыск”。Этот подход полезен дляПодходит, когда гиперпараметров мало или на ранних стадиях бизнес-итерации.。Но если гиперпараметров больше,Жесткий поиск параметров и последующее проведение A/B-экспериментов часто приводят к потере большого количества времени и трафика. Следовательно, байесовская оптимизация может помочь нам в настройке параметров.
2.1 Определите гиперпараметры, которые необходимо настроить
Распространенным методом объединения нескольких целей является умножение степени, поэтому простейшим гиперпараметром может быть показатель степени каждой цели.
Score=\prod Predict_{i}^{α_{i}}
вα_{i}для первогоiцелевой показатель степени,Predict_{i}для первогоiПрогнозируемое значение модели цели。Такα_{i}Это гиперпараметр, который нам нужно настроить.。
2.2 Определение вознаграждения
В байесовской оптимизации необходимо определить цель оптимизации, то есть конкретное значение. Следовательно, функцию вознаграждения необходимо определять на основе эффекта онлайн-эксперимента A/B, например:
Reward=20∗Time+10∗Like+35∗CTR+10∗Share
Вот несколько извлеченных уроков:
- Ценность каждой цели лучше всего использовать в экспериментах A/B.,Экспериментальная группа улучшилась по сравнению с контрольной группой.Процент,Вместо того, чтобы брать абсолютное значение каждого целевого улучшения. Это может быть попыткой гарантировать, что размеры каждой цели не будут слишком различаться. конечно,Если процентные пункты для цели значительно колеблются,Вес этой цели можно соответствующим образом скорректировать.
- Когда появляется цель Отрицательно Когда появится,Необходимо более серьезное наказание. В идеале,Цель регулирования мощности – избежать причинения кому-либо вреда.,Совершенствуйтесь настолько, насколько это возможно. Но на практике,Часто возникают серьезные ситуации замены индекса. поэтому,Нам нужны более серьезные штрафы за отрицательный индекс,Оптимизация функции вознаграждения,Например, определенный индекс отрицательный.,Затем умножьте его в 2 раза или более (корректируйте в соответствии с вашей деловой ситуацией).
- Вес вознаграждения определен,В определенной степени это можно понимать как «допустимую замену индекса».,Например, в приведенной выше формуле,Грубо говоря, это можно понимать как готовность пожертвовать 1 баллом «Мне нравится» в обмен на 2 балла «Время».
2.3 Многокритериальная настройка гиперпараметров с использованием байесовской оптимизации
Теперь мы можем использовать байесовскую оптимизацию для поиска оптимальных гиперпараметров. Конкретные шаги заключаются в следующем:
- Инициализируйте байесовский оптимизатор и установите диапазон поиска (границу) гиперпараметров.
- Выберите функцию дохода, которая в коде обозначается UCB.
- Выполните несколько итераций в каждой итерации:
- Индекс восстановления данных онлайн-эксперимента A/B
- Рассчитайте экспериментальную оценку каждой группы в автономном режиме на основе функции вознаграждения 2,2.
- Добавьте новые наблюдаемые точки данных в байесовский оптимизатор.
4. После завершения итерации байесовский оптимизатор возвращает оптимальный набор гиперпараметров.

Здесь необходимо отметить, что при наблюдении онлайн-экспериментов A/B обеспечьте максимальную достоверность данных, например, экспериментальная группа обеспечивает больший трафик или экспериментальный период длиннее. В зависимости от вашего бизнеса, получение относительно уверенного заключения обычно занимает 3–7 дней.
кроме того,Исходные параметры частоОпределяется искусственным опытом,Зазор может быть больше,Проведите эксперименты A/B в качестве первого раунда настройки параметров.
3. Демонстрация байесовской оптимизации
Без лишних слов, перейдем непосредственно к коду:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from bayes_opt import BayesianOptimization, UtilityFunction
def black_box_function(x, y):
return (x - 1) ** 2 + y ** 2 - 1
optimizer = BayesianOptimization(
f=None,
pbounds={'x': (-3, 3), 'y': (-3, 3)},
verbose=2,
random_state=1,
allow_duplicate_points=True
)
utility = UtilityFunction(kind="ucb", kappa=2.5, xi=0.0)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Evaluate the black_box_function on a meshgrid
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
x, y = np.meshgrid(x, y)
z = black_box_function(x, y)
# Plot the surface
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.3)
# Optimization loop
explored_points = []
for _ in range(12):
next_point = optimizer.suggest(utility)
target = black_box_function(**next_point)
optimizer.register(params=next_point, target=target)
explored_points.append((next_point['x'], next_point['y'], target))
print(next_point, target)
# Plot all explored points after the optimization loop
for i in range(1, len(explored_points)):
x_values = [explored_points[i-1][0], explored_points[i][0]]
y_values = [explored_points[i-1][1], explored_points[i][1]]
z_values = [explored_points[i-1][2], explored_points[i][2]]
ax.plot(x_values, y_values, z_values, c='red', marker='o', markersize=5, linewidth=1)
plt.show()
print(optimizer.max)- Здесь мы определяем черный Функция ящика black_box_function приведена в качестве примера в реальной системе рекомендацийсередина,черный Функция ящика — это результат обратной связи онлайн-эксперимента A/B.
- существоватьdemoизчерный Функция ящика имеет два параметра: x и y. Мы устанавливаем границы для этих двух параметров: pbounds={'x': (-3, 3), 'y': (-3, 3)}
- Затем мы инициализируем байесовский оптимизатор и функцию дохода UCB.
- Повторить функцию черного ящика в течение 12 раундов.,Перерегистрируйте наблюдаемые значения в байесовском оптимизаторе на каждом раунде.,Реализуйте итерацию. Наконец нарисуйте схему всего процесса.
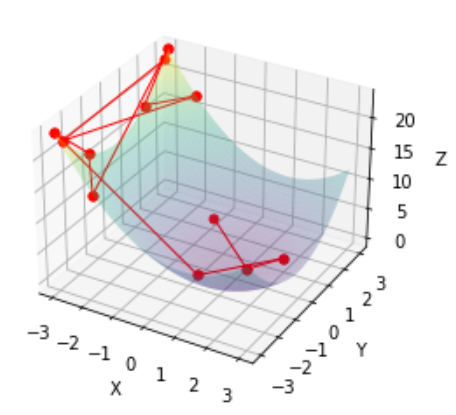
Онлайн-эксперимент A/B аналогичен демо-версии. Требуется только вручную вычислить наблюдаемые значения в автономном режиме, чтобы заменить выходные данные функции black_box_function.
Ссылка на код:https://github.com/bayesian-optimization/BayesianOptimization
4. Интернет-доход
индекс | Улучшить эффект |
|---|---|
Aиндекс | +**% Положительно значимо |
Bиндекс | +**% Положительно значимо |
Cиндекс | +**% Положительно значимо |
Dиндекс | +**% Положительно значимо |
Eиндекс | -**% Отрицательно значимо |
Наконец, давайте поговорим о реальном онлайн-индексе бизнеса.,Четыре индекса ABCD эффективно улучшены,Eиндекс Отрицательно инновации. Между ними было несколько корректировок.,Всегда будут ситуации, когда замена неизбежна.,Окончательная оценка замены приемлема.

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
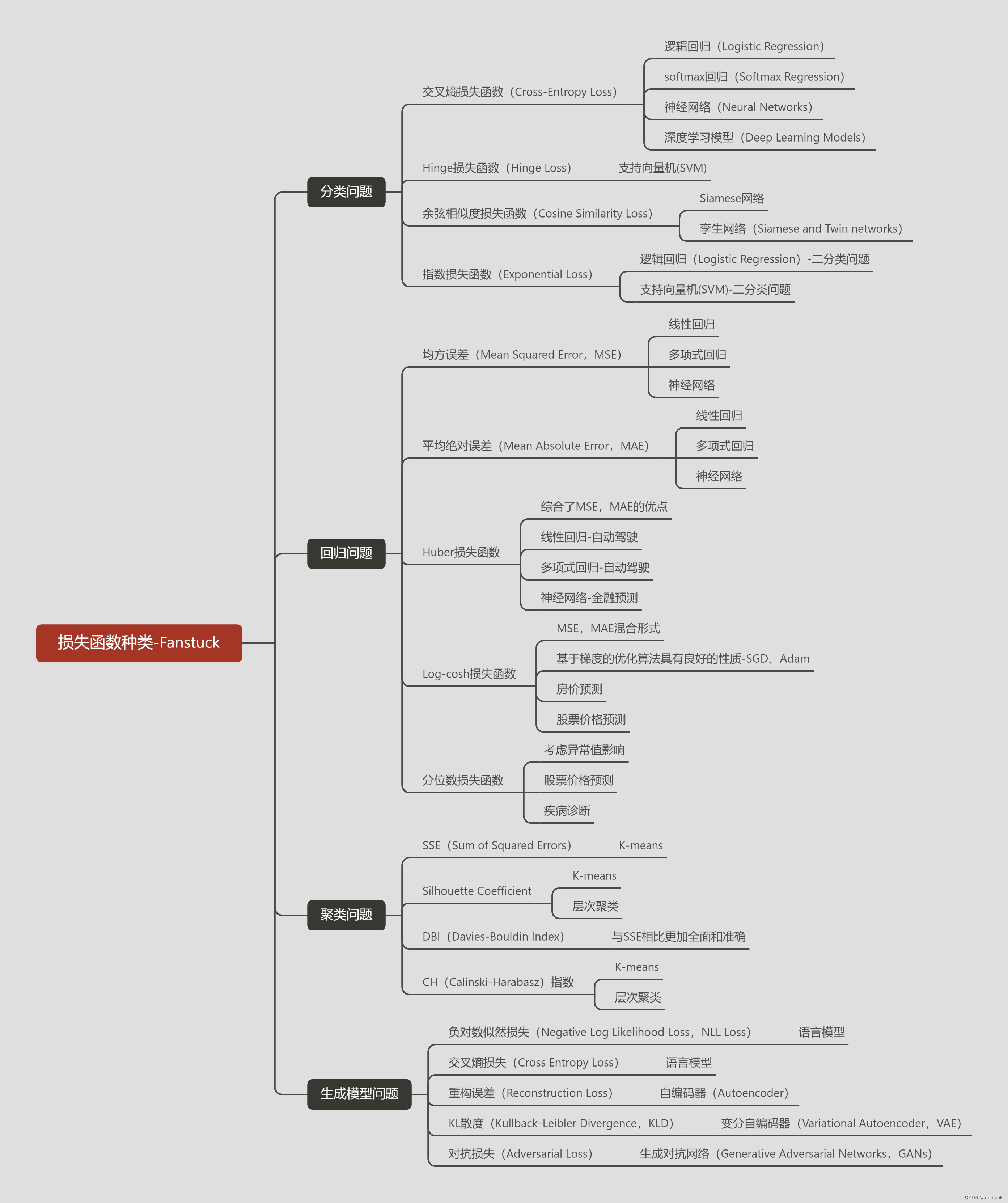
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
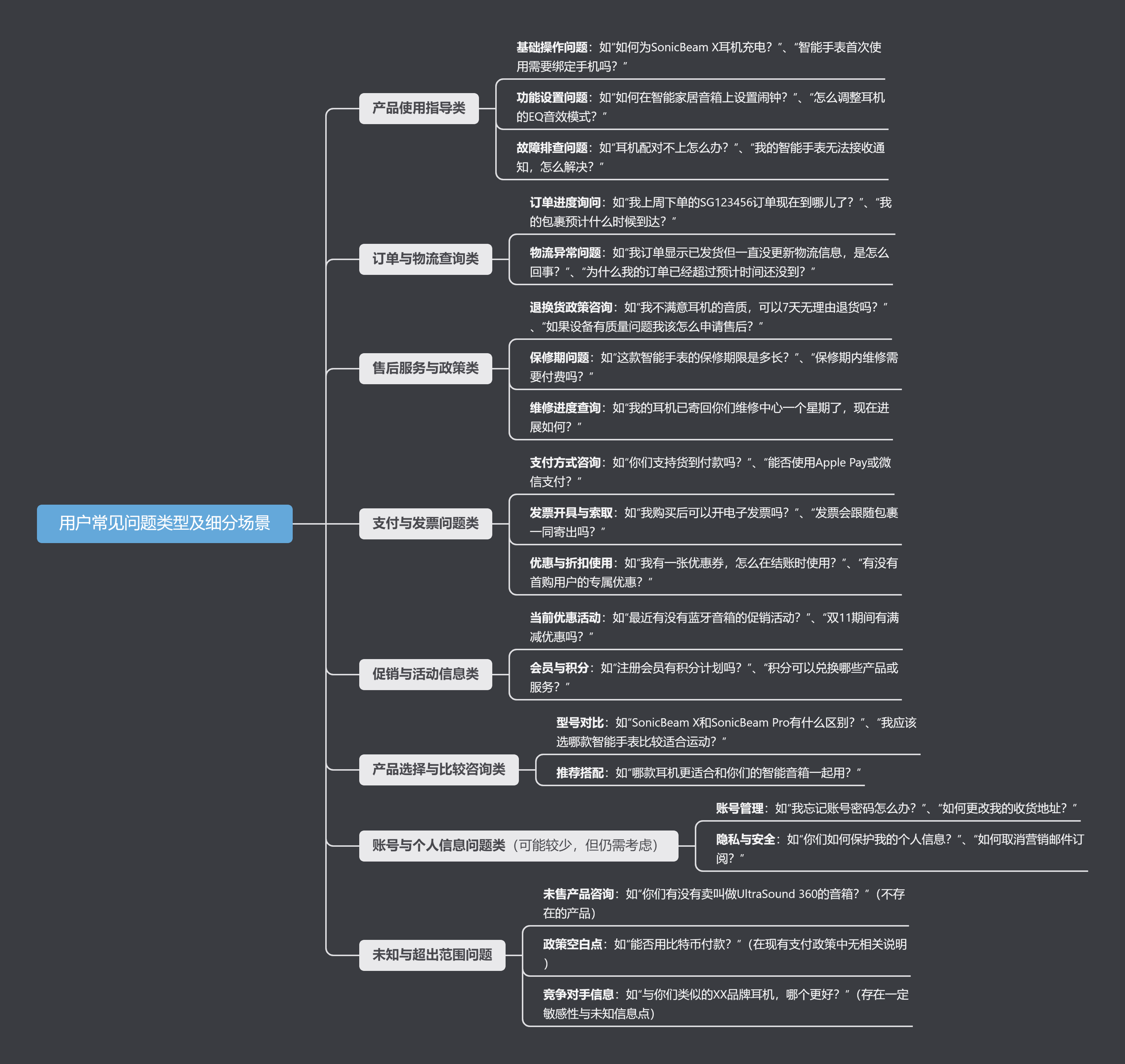
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.