Разобраться с алгоритмом ПИД-регулирования в одной статье (отказаться от формулы и по-настоящему понять ПИД-регулирование из принципа) «Рекомендуемый сборник»
Всем привет, мы снова встретились, я ваш друг Цюаньчжаньцзюнь.
Разберитесь с алгоритмом ПИД-регулирования в одной статье (откажитесь от формулы и по-настоящему поймите ПИД-регулирование в принципе)
ПИД-регулирование следует рассматривать как очень широко используемый алгоритм управления. ПИД-регулятор можно использовать для всего: от контроля температуры компонентов до управления ориентацией и скоростью полета дрона и т. д. Здесь мы понимаем ПИД-регулирование с принципиальной точки зрения. PID(proportion integration дифференциация) на самом деле относится к пропорции,интеграл,Дифференциальное управление. Сначала выложи картинки и формулы,Не имеет значения, если вы не понимаете。(Когда я впервые взглянул на этот алгоритм, я мог понять формулу, и знал, как ее использовать и как писать код, но я просто не знал принципа и не знал, зачем нужно использовать пропорция, дифференциал и интеграл для достижения наилучшего контроля. Почему это не работает? Каковы преимущества использования каждого элемента?)


В общем, когда выходные данные системы получены, выходные данные накладываются на входные с помощью трех методов работы: пропорционального, интегрального и дифференциального, тем самым управляя поведением системы. Для иллюстрации ниже используется простой пример.
алгоритм пропорционального управления
Давайте сначала поговорим о простейшем пропорциональном регулировании в ПИД-регуляторе.,Остальные два оставьте в стороне. Давайте воспользуемся классическим примером. Предположим, у меня есть резервуар для воды,Конечная цель контроля – обеспечить, чтобы уровень воды в резервуаре для воды всегда поддерживался на высоте 1 метр. Предполагая начальное время тестирования,Уровень воды в резервуаре для воды составляет 0,2 метра.,Тогда возникает ошибка между уровнем воды в текущий момент и целевым уровнем воды.,И ошибка на данный момент 0,8.,Предположим, рядом с вами стоит человек,Этот человек контролирует уровень воды, добавляя воду в резервуар. Если вы просто используете алгоритм пропорционального управления означает, что количество добавленной воды прямо пропорционально ошибке ошибки. Прямо сейчас u=kp*error Предположим, что kp равно 0,5, Тогда, когда t=1 (имеется в виду первый раз, когда добавляется вода, то есть первый раз, когда в системе применяется управление), тогда u=0,5*0,8=0,4, поэтому количество воды, добавленной в этот раз, приведет к повышению уровня воды. повыситься на 0,4 из базы 0,2, достигнув 0,6. Тогда в момент времени t=2 (применяется второй контроль времени) текущий уровень воды равен 0,6, поэтому ошибка равна 0,4. u=0,5*0,4=0,2, что приведет к повторному повышению уровня воды на 0,2–0,8. Если цикл продолжается таким образом, это алгоритм пропорционального Как управлять управлением. Как видите, конечный уровень воды достигнет нужного нам 1 метра. Однако пропорциональное управление само по себе имеет некоторые недостатки, одним из которых является – Устойчивая ошибка! (Я тоже много читал и долго думал об этом, прежде чем понял, что такое установившаяся ошибка и почему существует установившаяся ошибка). Как и в приведенном выше примере, в зависимости от значения kp система в конечном итоге достигнет 1 метра, и установившейся ошибки не будет. Однако рассмотрим другую ситуацию. Предположим, что резервуар для воды протекает во время добавления воды. Предположим, что при каждом добавлении воды будет вытекать 0,1 метра воды. Еще предположим, что kp равно 0,5, то возникнет определенная ситуация. Допустим, после нескольких доливов воды, когда уровень воды в резервуаре для воды достигнет 0,8, уровень воды больше не изменится! ! ! Поскольку уровень воды равен 0,8, ошибка = 0,2. Следовательно, количество воды, добавляемой каждый раз в резервуар для воды, равно u=0,5*0,2=0,1. При этом каждый раз из резервуара будет вытекать 0,1 метра воды! ! ! Добавленная и вытекшая вода уравновешиваются, и уровень воды больше не изменится! ! Другими словами, моя цель — 1 метр, но когда система наконец достигает 0,8 метра, уровень воды больше не меняется, и система достигла стабильности. Результирующая ошибка является установившейся ошибкой. (В реальных ситуациях чаще встречается ситуация, аналогичная утечке воды в резервуаре для воды. Например, при управлении движением автомобиля сопротивление трения эквивалентно «утечке воды». При управлении полетом робота рука или дрон, все виды сопротивления и расхода можно понять в данном примере как "утечка воды"). Следовательно, во многих случаях только пропорциональное управление не может удовлетворить этим требованиям.
Интегральный алгоритм управления
Все еще используя приведенный выше пример,Если вы используете только пропорцию,Можно обнаружить, что существует временная ошибка,Конечный уровень воды застрял на отметке 0,8. затем,под контролем,Вводим еще один компонент,Эта составляющая прямо пропорциональна ошибке. так,Пропорция+Интегральный алгоритм управлениядля: u=kp*error+ ki ∗∫ ∗ ∫ *\interror Продолжая использовать приведенный выше пример для иллюстрации, первая ошибка равна 0,8, а вторая ошибка равна 0,4. На этом этапе интеграл ошибки (интеграция в дискретных случаях фактически представляет собой накопление) ∫ ∫ \interror=0.8+0.4=1.2. Управляющей величиной в это время, помимо пропорциональной части, является еще и коэффициент ki, умноженный на интегральный член. Поскольку этот интегральный член будет накапливать предыдущие ошибки, он может эффективно устранить установившуюся ошибку (при условии, что, когда есть только пропорциональный член, система застревает на установившейся ошибке, которая в приведенном выше примере равна 0,8. Поскольку Добавление существования интегрального члена увеличит входные данные, так что уровень воды в резервуаре для воды может превысить 0,8 и постепенно достичь целевого значения 1,0.) В этом роль интегрального члена.
Алгоритм дифференциального управления
В качестве другого примера рассмотрим ситуацию с торможением. Управляйте автомобилем плавно. Когда вы видите впереди красный свет, чтобы ехать плавно, вы просто отпускаете педаль газа и нажимаете на тормоза на десятки метров вперед. Если автомобиль находится очень близко к парковочной линии, резко затормозите, чтобы остановить автомобиль. Весь процесс можно рассматривать как стратегию управления, добавляющую дифференциал. Дифференциал, если говорить прямо, в дискретных случаях — это разница ошибок, то есть разница между ошибкой в момент времени t и в момент t-1, то есть u=kd*(error(t)-error(t-1 )), где kd — коэффициент A. Видно, что во время процесса торможения, поскольку ошибка становится все меньше и меньше, член дифференциального управления должен быть отрицательным числом. Добавление отрицательного числа к управлению предназначено для предотвращения проезда автомобиля из-за отсутствия торможения. время вне линии. Из здравого смысла можно понять, что чем ближе автомобиль к парковочной линии, тем больше внимания следует уделять торможению и недопущению пересечения автомобилем линии. Поэтому функцию этого дифференциального термина можно понимать как торможение. автомобиль находится очень близко к парковочной линии, а скорость по-прежнему очень высока. Когда абсолютное значение этого дифференциального члена (на самом деле отрицательное число) будет очень большим, а это означает, что тормоза следует задействовать сильнее, чтобы остановить автомобиль. . Переходя к приведенному выше примеру добавления воды в резервуар для воды, когда обнаруживается, что уровень воды в резервуаре для воды близок к 1, добавление дифференциального члена может предотвратить добавление воды в резервуар для воды на высоту более 1 метр Грубо говоря, сокращает время в процессе контроля.
Теперь, оглядываясь назад на эту формулу, становится очень ясно:

Первый член в скобках — это пропорциональный член, второй член — интегральный член, а третий член — дифференциальный член. Первый член — это просто коэффициент. Во многих случаях его необходимо использовать только в дискретные моменты времени, а управление можно свести к


Перед каждым пунктом стоят коэффициенты. Эти коэффициенты нужно попробовать и определить в экспериментах. Для удобства эти коэффициенты унифицированы:

Это делает его намного понятнее, и перед каждым членом пропорциональности, дифференциала и интеграла стоит коэффициент, а дискретная формула очень подходит для реализации программирования. На этом принципы и методы ПИД закончены, а остальное – практика. В реальной инженерной практике сложнее всего определить коэффициенты трех слагаемых, для определения которых требуется много экспериментов и опыта. Путем непрерывных проб и правильного мышления можно выбрать подходящие коэффициенты и получить отличный контроллер.
Издатель: Лидер стека программистов полного стека, укажите источник для перепечатки: https://javaforall.cn/134794.html Исходная ссылка: https://javaforall.cn
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
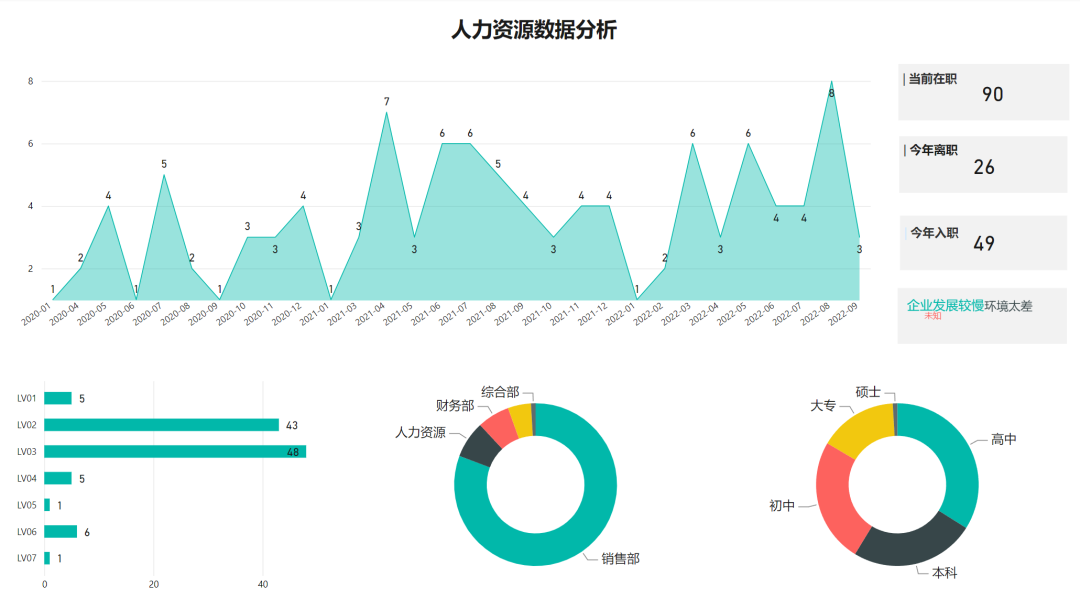
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
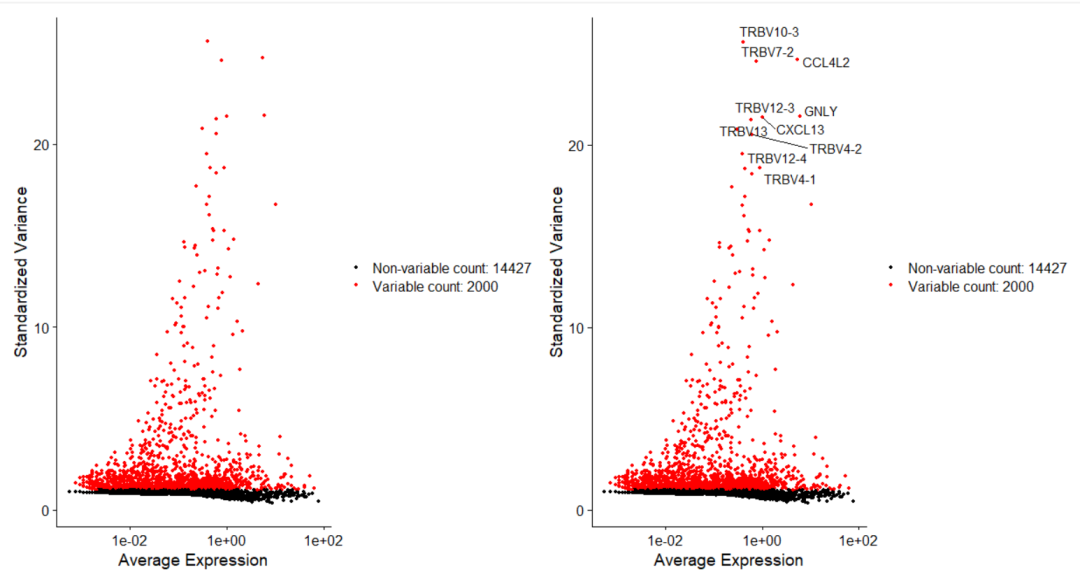
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
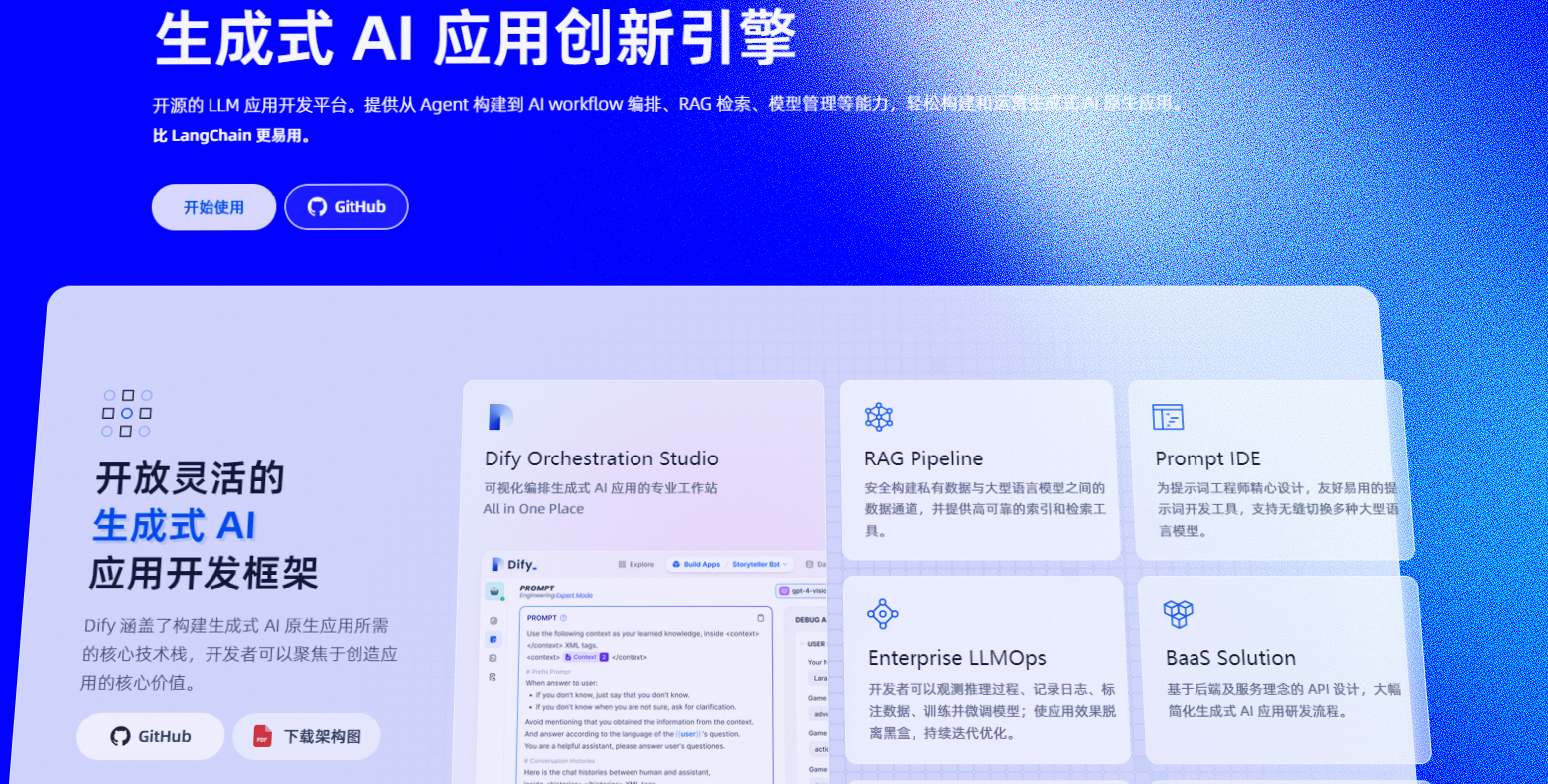
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
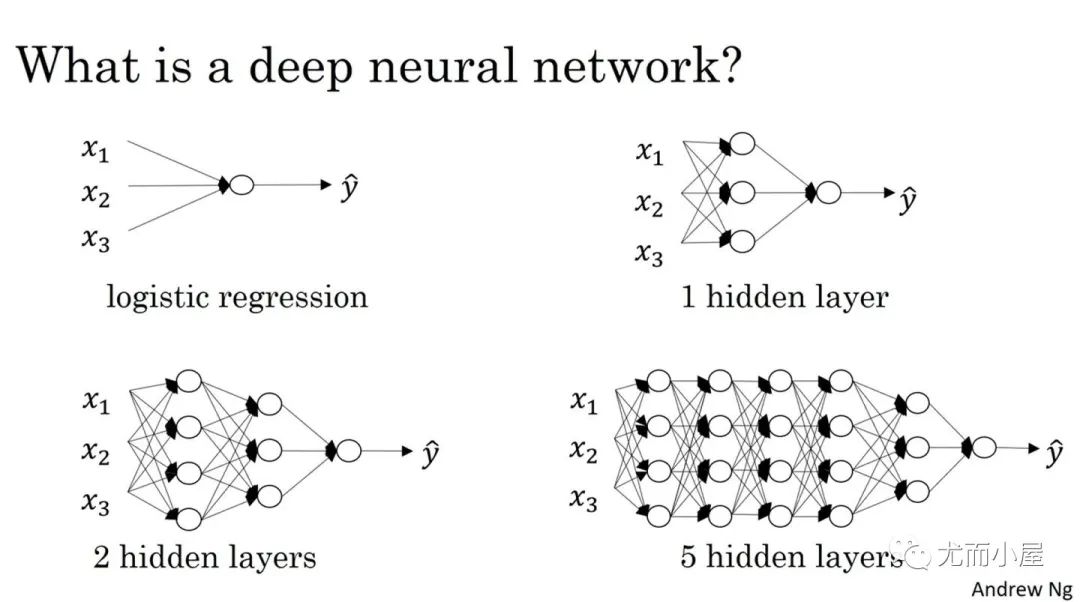
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


