Проектирование фильтра Matlab: примеры реализации КИХ-фильтра и БИХ-фильтра
Проектирование фильтра Matlab: примеры реализации КИХ-фильтра и БИХ-фильтра
!! ✨ Версия Matlab — R2022b, совместимая с предыдущими версиями. Выдержки из этой статьи обобщены в: Введение в практику проектирования цифровых фильтров. - MATLAB & Simulink Example - MathWorks Китай.
В этой статье используется Signal в Matlab. Processing Toolboxвdesignfiltфункция,И реализовать следующие два типа в зависимости от частотной характеристикифильтр:
- КИХ-фильтр: фильтр с конечной импульсной характеристикой, также известный как нерекурсивный фильтр;
- БИХ-фильтр:бесконечные числа импульсной характеристики(Infinite Impulse Response) фильтр, также известный как рекурсивный фильтр.
1. Конструкция КИХ-фильтра
1.1 Введение в конструкцию фильтра нижних частот
Фактическая конструкция КИХ-фильтра обычно включает следующие три параметра:
Transition width:ширина переходной зоны;Peak passband/stopband ripple:Максимальная неравномерность полосы пропускания и полосы задерживания;Filter order:Порядок фильтра(Выбор длины усеченной импульсной характеристики)。
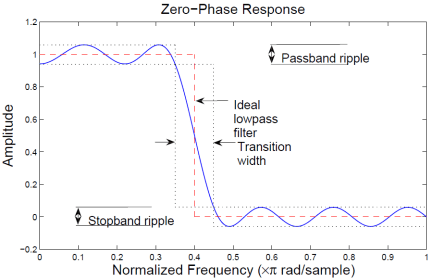
Как правило, идеальный КИХ-фильтр нижних частот невозможно спроектировать, поскольку импульсная характеристика, необходимая для достижения идеального фильтра нижних частот, бесконечно длинна. Аппроксимация идеальной импульсной характеристики с конечной длиной вызывает неравномерность как в полосе пропускания, так и в полосе задерживания фильтра, что приводит к ненулевой ширине полосы перехода между полосой пропускания и полосой задерживания.
При проектировании фильтра неравномерность полосы пропускания/полосы задерживания и ширина полосы перехода являются отклонениями от идеального фильтра нижних частот, как показано на рисунке ниже:
Преимущества FIR-фильтров:
- Его производительность очень стабильна;
- Его можно спроектировать как фильтр с линейной фазой.
Однако КИХ-фильтры по-прежнему могут иметь длительные переходные характеристики, что может привести к увеличению вычислительных затрат для решения некоторых задач.
1.2 Конструкция КИХ-фильтра минимального заказа
Разработка КИХ-фильтра минимального заказа в основном включает в себя следующие два этапа:
- Путем указания частоты полосы пропускания/полосы задерживания, пульсаций в полосе пропускания и затухания в полосе задерживания.,мы можем получить Проектирование КИХ-фильтра минимального заказа。
- Алгоритм проектирования выберет минимальную длину фильтра, соответствующую установленному КИХ-фильтру.

Код Matlab выглядит следующим образом,проходитьdesignfiltфункциявыполнить,и пройтиfvtoolфункция Проверятьразработанныйнизкий проходFIRфильтр Амплитудный отклик:
Fpass = 0.3; % Частотный коэффициент полосы пропускания
Fstop = 0.43; % Коэффициент частоты стоп-диапазона
Ap = 1; % пульсация в полосе пропускания
Ast = 30; % Затухание в полосе задерживания
% Разработка КИХ-фильтра нижних частот с помощью функции designfilt
d = designfilt('lowpassfir', ... % фильтр нижних частот
'PassbandFrequency', Fpass, ... % Частота полосы пропускания
'StopbandFrequency', Fstop, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast); % Затухание в полосе задерживания
% Амплитудный отклик КИХ-фильтра нижних частот, разработанный с помощью функции fvtool
hfvt = fvtool(d);
Результаты выполнения кода следующие:
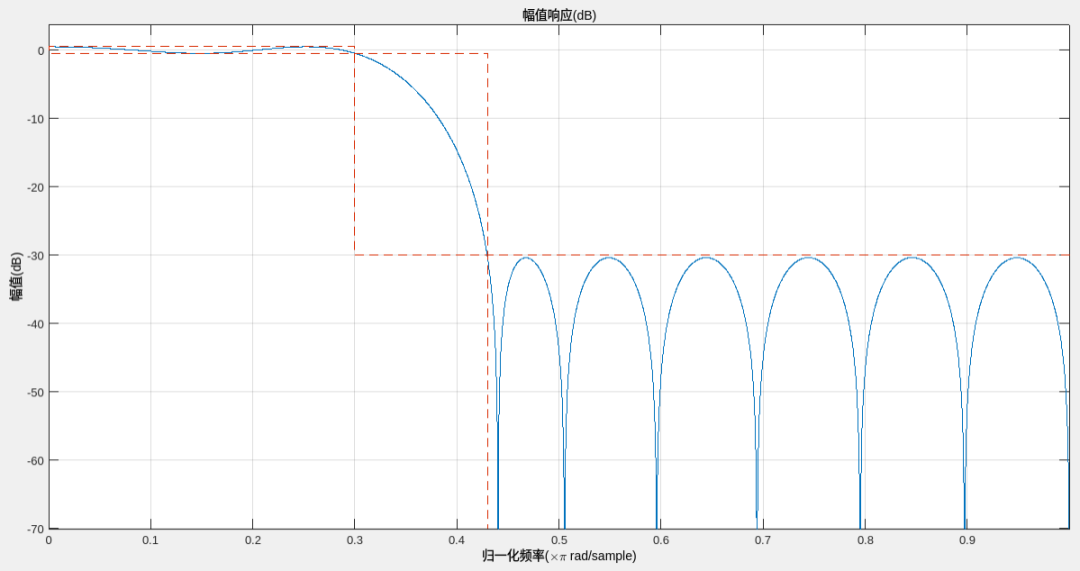
!! проходить
filtordфункция Может Проверятьгенерироватьизфильтрпорядок,Как показано ниже,разработанныйфильтрdпорядокглаздля19:

Уведомление: кроме того,fvtoolфункцияоткроется Фильтрация визуализацииинструмент,проходить Долженинструмент箱我们Может Проверятьразработанныйфильтр Следующие различные результаты анализа:
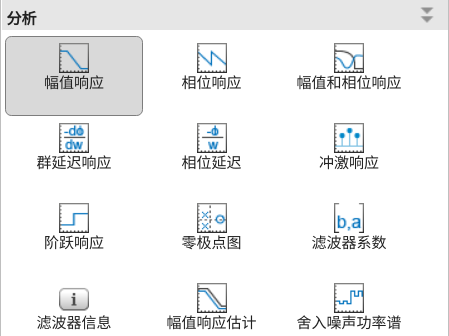
!!
designfiltфункция По умолчанию выбран один Равная рябь(линейная фаза)алгоритм проектированияEquiripple,Можетпроходить Заказinfo(d)Проверятьфильтрполученная информацияфильтралгоритм проектирования。в целом,Фильтр пульсаций линейной фазы позволяет достичь идеальных результатов.,Это связано с заданным порядком для,линейное поведениефильтри идеалфильтр Максимально возможное отклонение。
- 🚀 Уведомление: в целом,Мы также можем использовать
Kaiserоконное усиление Проектирование КИХ-фильтра минимального заказа。ХотяKaiserокнов целомстанет большеиз Порядок фильтра,Но этот алгоритм имеет меньшие вычислительные затраты.,И проблемы конвергенции возникают реже.
В приведенном ниже коде используетсяKaiserДизайн оконного метода такой же, как указано выше.фильтр,И с равной пульсациейфильтр(Equirippleалгоритм)Амплитудный откликсравнивать:
% проходитьKaiserреализация окнаFIRфильтр нижних Дизайн по частоте
dk = designfilt('lowpassfir', ... % фильтр нижних частот
'PassbandFrequency', Fpass, ... % Частота полосы пропускания
'StopbandFrequency', Fstop, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'DesignMethod', 'kaiserwin'); % Проектирование фильтра с использованием метода окна Кайзера
% т.е. добавьте фильтр dk к результату графика
addfilter(hfvt, dk);
% Добавить легенду
legend(hfvt, «Алгоритм проектирования фильтра Equiripple», «Алгоритм проектирования оконного фильтра Кайзера»)
Результат выполнения кода показан на рисунке ниже:

проходитьfiltord(dk)Может Проверять Порядок фильтрадля24:
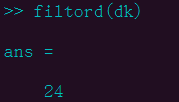
1.3 Установка параметров частоты фильтра в герцах

Fpass = 350; % Частота полосы пропускания
Fstop = 400; % частота полосы задерживания
Ap = 1; % пульсация в полосе пропускания
Ast = 30; % Затухание в полосе задерживания
Fs = 2000; % Частота дискретизации
% Разработка КИХ-фильтра нижних частот с помощью функции designfilt
d = designfilt('lowpassfir', ... % фильтр нижних частот
'PassbandFrequency', Fpass, ... % Частота полосы пропускания
'StopbandFrequency', Fstop, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'SampleRate', Fs); % Частота дискретизации
% Амплитудный отклик КИХ-фильтра нижних частот, разработанный с помощью функции fvtool
hfvt = fvtool(d);
Результат выполнения кода показан на рисунке ниже:
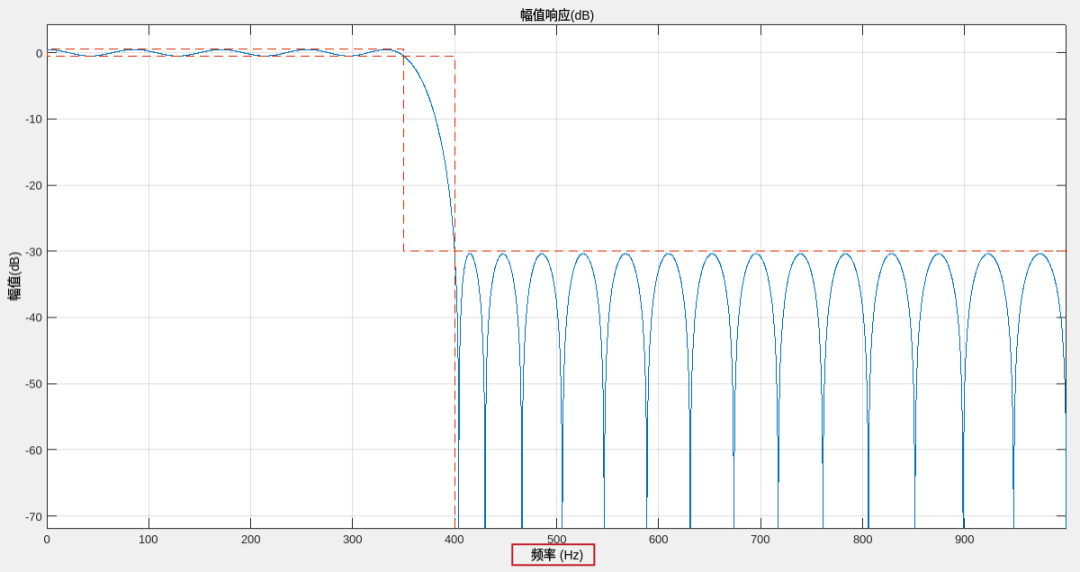
1.4. Проектирование КИХ-фильтра с фиксированным порядком и фиксированной полосой пропускания полосы перехода.
В этом разделе используются равные пульсации.фильтралгоритм(Equirippleалгоритм)и метод наименьших квадратов(Least squareалгоритм)Два видафильтралгоритм проектирования,Дизайн имеет фиксированный порядок、фиксированная ширина полосы переходаFIRфильтр。

Код Matlab выглядит следующим образом:
N = 30; % Порядок фильтра
Fpass = 400; % Частота полосы пропускания
Fstop = 450; % частота полосы задерживания
Fs = 2000; % Частота дискретизации
% Спроектируйте deq КИХ-фильтра, используя алгоритм проектирования фильтра equiripple по умолчанию.
deq = designfilt('lowpassfir', ... % КИХ-фильтр нижних частот
'FilterOrder', N, ... % Порядок фильтра
'PassbandFrequency', Fpass, ... % Частота полосы пропускания
'StopbandFrequency', Fstop, ... % частота полосы задерживания
'SampleRate', Fs); % Частота выборки
% Спроектируйте deq FIR-фильтра с использованием алгоритма проектирования фильтра ls по методу наименьших квадратов
dls = designfilt('lowpassfir', ... % КИХ-фильтр нижних частот
'FilterOrder', N, ... % Порядок фильтра
'PassbandFrequency', Fpass, ... % Частота полосы пропускания
'StopbandFrequency', Fstop, ... % частота полосы задерживания
'SampleRate', Fs, ... % Частота выборки
'DesignMethod', 'ls'); % Алгоритм построения фильтра методом наименьших квадратов
% Фильтрация визуализации
hfvt = fvtool(deq, dls);
legend(hfvt, «Алгоритм проектирования фильтра Equiripple», 'Алгоритм построения фильтра методом наименьших квадратов');
Результат выполнения кода показан на рисунке ниже:
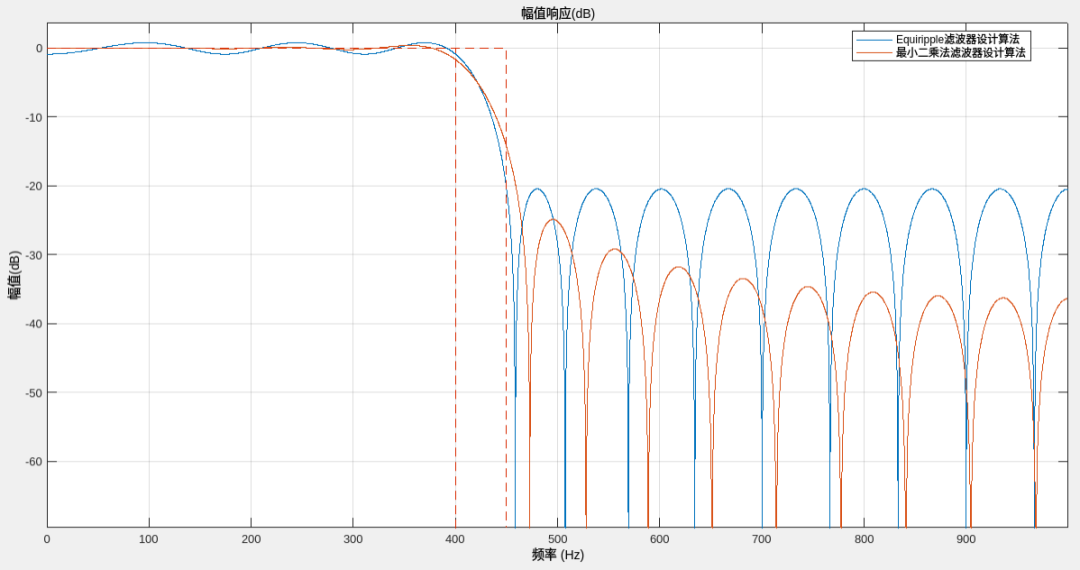
!! ✨ проиллюстрировать:
- Равная рябьфильтр Идеально подходит для ситуаций, когда соблюдаются определенные допуски.,Например, разработка фиксированной минимальной полосы задерживания、ослабленныйфильтр;Но методдля Хотите минимизировать полосу пропускания/стоп-полосавэнергия ошибкиизвопрос,Результаты обычно далеки от идеальных.
- Если мы хотим минимизировать энергию сигнала в определенной полосе частот, используйте метод наименьших квадратов для разработки алгоритма.
1.5 Конструкция КИХ-фильтра с фиксированным порядком и фиксированной частотой среза
- Мы можем использовать метод проектирования окон для проектирования фиксированного Порядок фильтраичастота срезаизфильтр,То есть мы можем использовать разные окна (например,,Hamming、Chebyshevокно и т. д.)контролировать Затухание в полосе задерживания,И оставьте порядок неизменным.

Код Matlab выглядит следующим образом:
% Конструкция КИХ-фильтра окна Хэмминга
dhamming = designfilt('lowpassfir', ... % КИХ-фильтр нижних частот
'FilterOrder', 50, ... % Порядок фильтра
'CutoffFrequency', 100, ... % частота среза
'SampleRate', 1000, ... % Частота дискретизации
'Window', 'hamming'); % Функция окна Хэмминга
% Конструкция КИХ-фильтра окна Чебышева
dchebwin = designfilt('lowpassfir', ... % КИХ-фильтр нижних частот
'FilterOrder', 50, ... % Порядок фильтра
'CutoffFrequency', 100, ... % частота среза
'SampleRate', 1000, ... % Частота дискретизации
'Window', {'chebwin', 90}); % Оконная функция Чебышева с затуханием боковых лепестков 90
% Фильтрация Визуализации и их сравнение
hfvt = fvtool(dhamming, dchebwin);
legend(hfvt, «Окно Хэмминга», «Окно Чебышева»)
Результат выполнения кода показан на рисунке ниже:

2. Конструкция БИХ-фильтра
2.1 Знакомство с БИХ-фильтрами
- Недостатки КИХ-фильтров в основном выражаются в: его потребность великаиз Порядок фильтр может соответствовать фактическому дизайну,тем самым увеличивая потребность в вычислениях,В это время для решения проблемы можно использовать БИХ-фильтр.
!! Идеи конструкции БИХ-фильтра: Если пульсация остается постоянной, порядок фильтра обратно пропорционален полосе пропускания фильтра. Благодаря обратной связи можно спроектировать фильтр, соответствующий требованиям, используя фильтр очень малого порядка. Бесконечная импульсная характеристика IIR (Бесконечная Impulse Смысл Response): когда на фильтр подается импульс, выходной сигнал никогда не спадает до нуля.
БИХ-фильтры полезны, когда вычислительные ресурсы ограничены. Однако стабильные причинные БИХ-фильтры не могут обеспечить идеально линейную фазу. Избегайте использования БИХ-схем, где требуется линейность фазы. Другая важная причина использования БИХ-фильтров заключается в том, что БИХ-фильтры имеют меньшую групповую задержку и, следовательно, более короткую переходную характеристику по сравнению с КИХ-фильтрами.
Обычно используемые БИХ-фильтры включают: фильтр Баттерворта, фильтр Чебышева типа I, фильтр Чебышева типа I и эллиптический фильтр. Их основные характеристики, а также сходства и различия приведены в таблице ниже:
БИХ-фильтр | Функции |
|---|---|
Фильтр Баттерворта | БИХ-фильтр с максимальной плоскостностью,Но это приводит к увеличению ширины переходной зоны,и нужен большийиз Порядок фильтрауменьшить переходную зонуизширина。 |
Фильтр Чебышева I типа | проходитьпозволятьпульсация в полосе пропускания,Фильтр Чебышева I Ширина переходной зоны у типа меньше, чем у того же заказа. Фильтр Баттерворта。Butterworth и Chebyshev I добрыйфильтриметь самый плоскийизстоп-полоса。дляданныйиз Порядок фильтра,Потребность в пульсации в полосе пропусканияиширина переходной зоныкомпромисс между。 |
Фильтр Чебышева II типа | Он имеет самую плоскую полосу пропускания и равную гофрированную полосу задерживания. В связи с реальной ситуацией,Обычно очень большое затухание не требуется.,Поэтому можно допустить некоторую неравномерность полосы задерживания.,в обмен на использование меньшего заказа,для получения пропускной способности перехода, отвечающей спросу. |
Эллиптический фильтр | Чтопроходитьпозволять通带и Пульсация в полосе задерживания для обобщенияButterworthиChebyshevфильтр。С рябьюизуменьшать,Эллиптический фильтр Может быть приближен к любомуButterworthиChebyshevфильтриз Амплитудаи Фазовый отклик。 |
2.2 Реализация и сравнение производительности БИХ-фильтра

Например 4, используйте Фильтр соответственно. Баттерворта、Chebyshev I Фильтр классов, Чебышев I Фильтр классов и Эллиптический фильтрчетыре вида БИХ-фильтрметод проектирования。и сравнить соответственночетыре видаметодиз Следующие три аспектаизфильтр Параметры производительности:
- порядок фильтра;
- отклик фильтра;
- Сравнение групповых задержек;
(1) Реализация четырех фильтров
Код Matlab выглядит следующим образом:
Fp = 100; % Частота полосы пропускания
Fst = 250; % частота полосы задерживания
Ap = 1; % пульсация в полосе пропускания
Ast = 60; % Затухание в полосе задерживания
Fs = 2e3; % Частота дискретизации
% Butterworth фильтр
dbutter = designfilt('lowpassiir', ... % IIRфильтр нижних частот
'PassbandFrequency', Fp, ... % Частота полосы пропускания
'StopbandFrequency', Fst, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'SampleRate', Fs, ... % Частота дискретизации
'DesignMethod', 'butter'); % Фильтр Баттерворта
% Фильтр Чебышева I типа
dcheby1 = designfilt('lowpassiir', ... % IIRфильтр нижних частот
'PassbandFrequency', Fp, ... % Частота полосы пропускания
'StopbandFrequency', Fst, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'SampleRate', Fs, ... % Частота дискретизации
'DesignMethod', 'cheby1'); % Фильтр Чебышева I типа
% Фильтр Чебышева II типа
dcheby2 = designfilt('lowpassiir', ... % IIRфильтр нижних частот
'PassbandFrequency', Fp, ... % Частота полосы пропускания
'StopbandFrequency', Fst, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'SampleRate', Fs, ... % Частота дискретизации
'DesignMethod', 'cheby2'); % Фильтр Чебышева II типа
% Эллиптический фильтр
dellip = designfilt('lowpassiir', ... % IIRфильтр нижних частот
'PassbandFrequency', Fp, ... % Частота полосы пропускания
'StopbandFrequency', Fst, ... % частота полосы задерживания
'PassbandRipple', Ap, ... % пульсация в полосе пропускания
'StopbandAttenuation', Ast, ... % Затухание в полосе задерживания
'SampleRate', Fs, ... % Частота дискретизации
'DesignMethod', 'ellip'); % Эллиптический фильтр
(2) Сравнение порядков четырех фильтров.
Код Matlab выглядит следующим образом:
% Сравните четыре IIR фильтрпорядок
FilterOrders = [filtord(dbutter) filtord(dcheby1) filtord(dcheby2) filtord(dellip)]
Результат выполнения кода показан на рисунке ниже:

По результатам выполнения кода видно, что для одних и тех же установленных ограничений метод Баттерворта выдает наивысший порядок, а эллиптический метод — минимальный порядок.
(3) Сравнение откликов четырех фильтров.
Код Matlab выглядит следующим образом:
% Сравните четыре IIR фильтризответ
hfvt = fvtool(dbutter,dcheby1,dcheby2,dellip);
axis([0 1e3 -80 2]);
Результат выполнения кода показан на рисунке ниже:
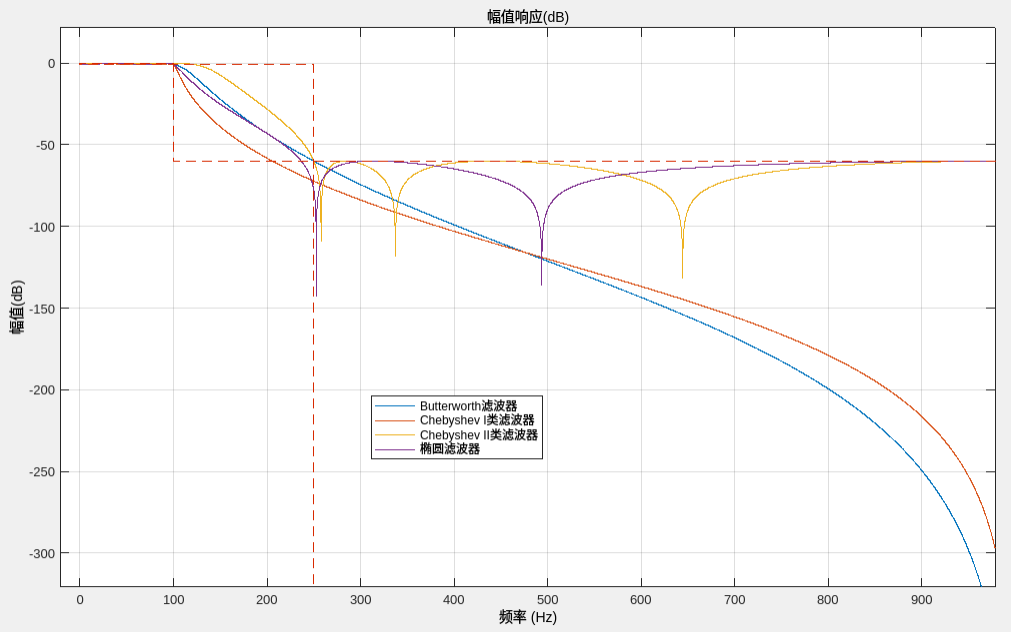
(4) Сравнение групповых задержек четырех фильтров.
для IIR При использовании фильтров нам необходимо учитывать не только компромисс между пульсацией и шириной полосы перехода, но и степень фазовых искажений. В общем, это связано с невозможностью иметь линейную фазу на всем интервале Найквиста. Таким образом, вы можете увидеть, насколько далека фазовая характеристика от линейной, взглянув на групповую задержку (в идеале постоянную) и увидев, насколько она ровная.
Код Matlab выглядит следующим образом:
% Сравниватьчетыре видафильтризгрупповая задержка
hfvt = fvtool(dbutter,dcheby1,dcheby2,dellip,'Analysis','grpdelay');
legend(hfvt,'Фильтр Баттерворта', 'Chebyshev Type Iфильтр', 'Chebyshev Type IIфильтр','Эллиптический фильтр')
Результат выполнения кода показан на рисунке ниже:
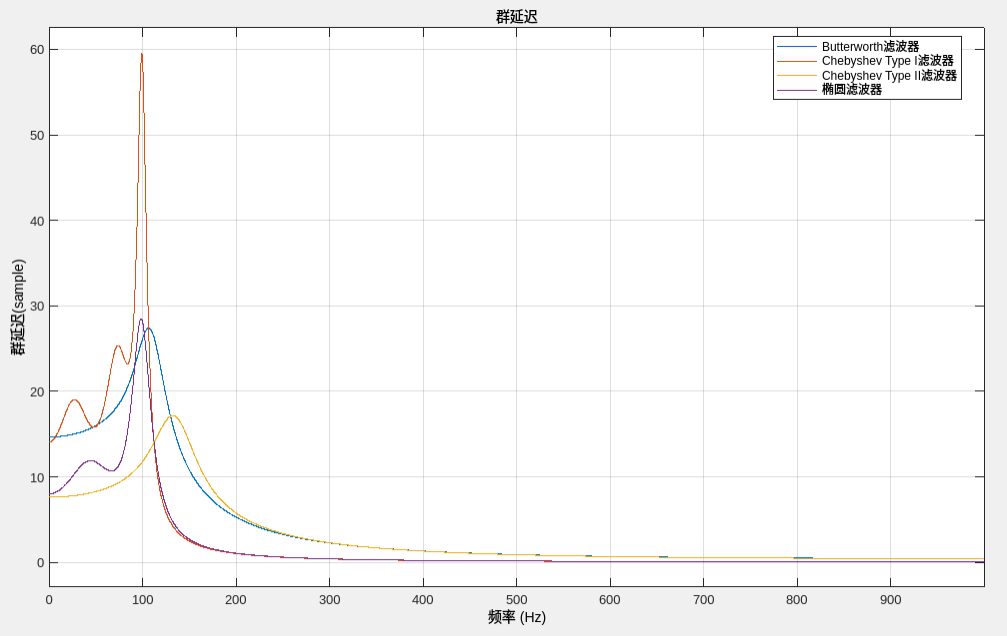
Как видно на картинке выше, Баттерворт и Chebyshev II Проект класса имеет самую плоскую групповую задержку, что вносит наименьшие искажения.

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
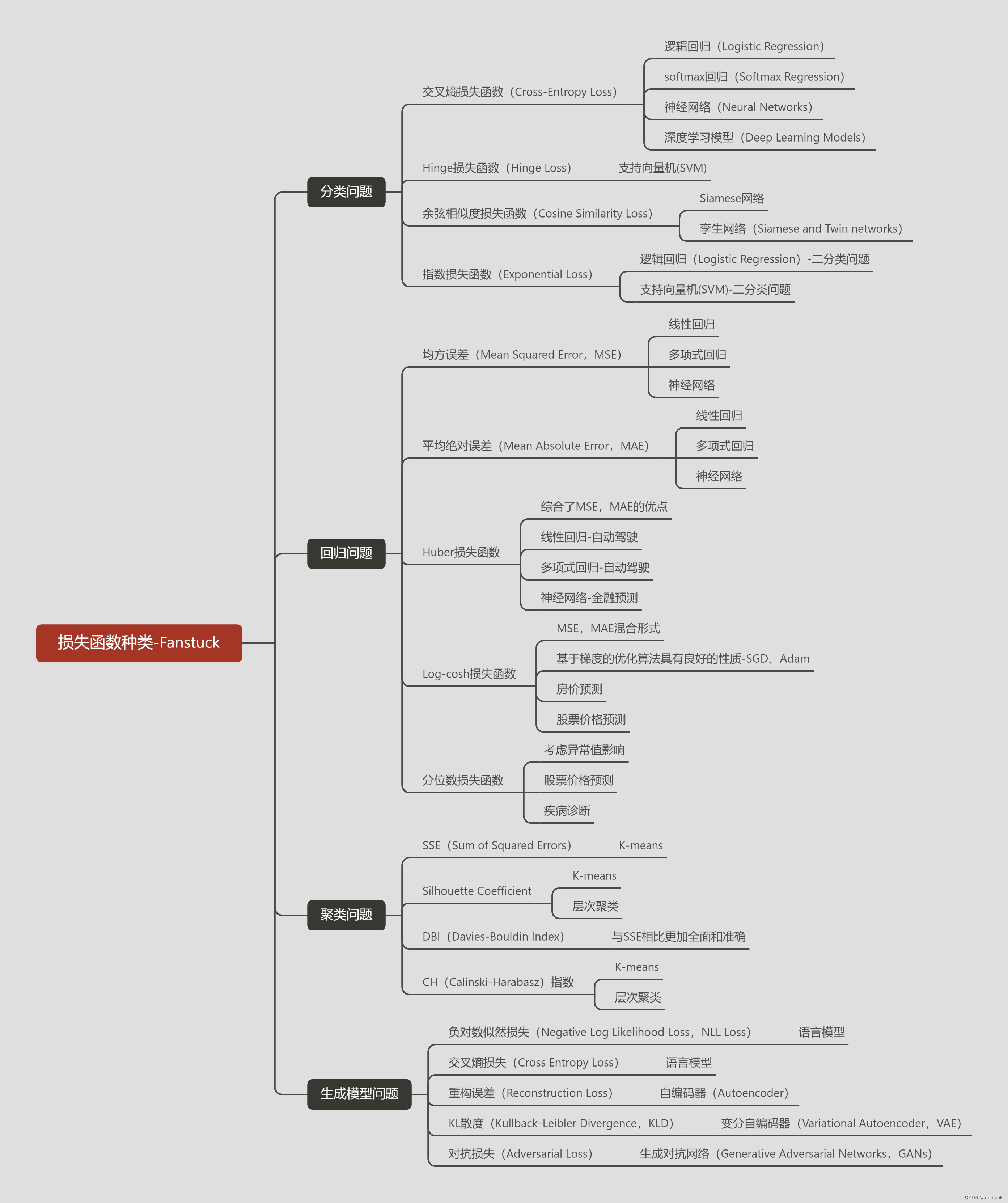
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
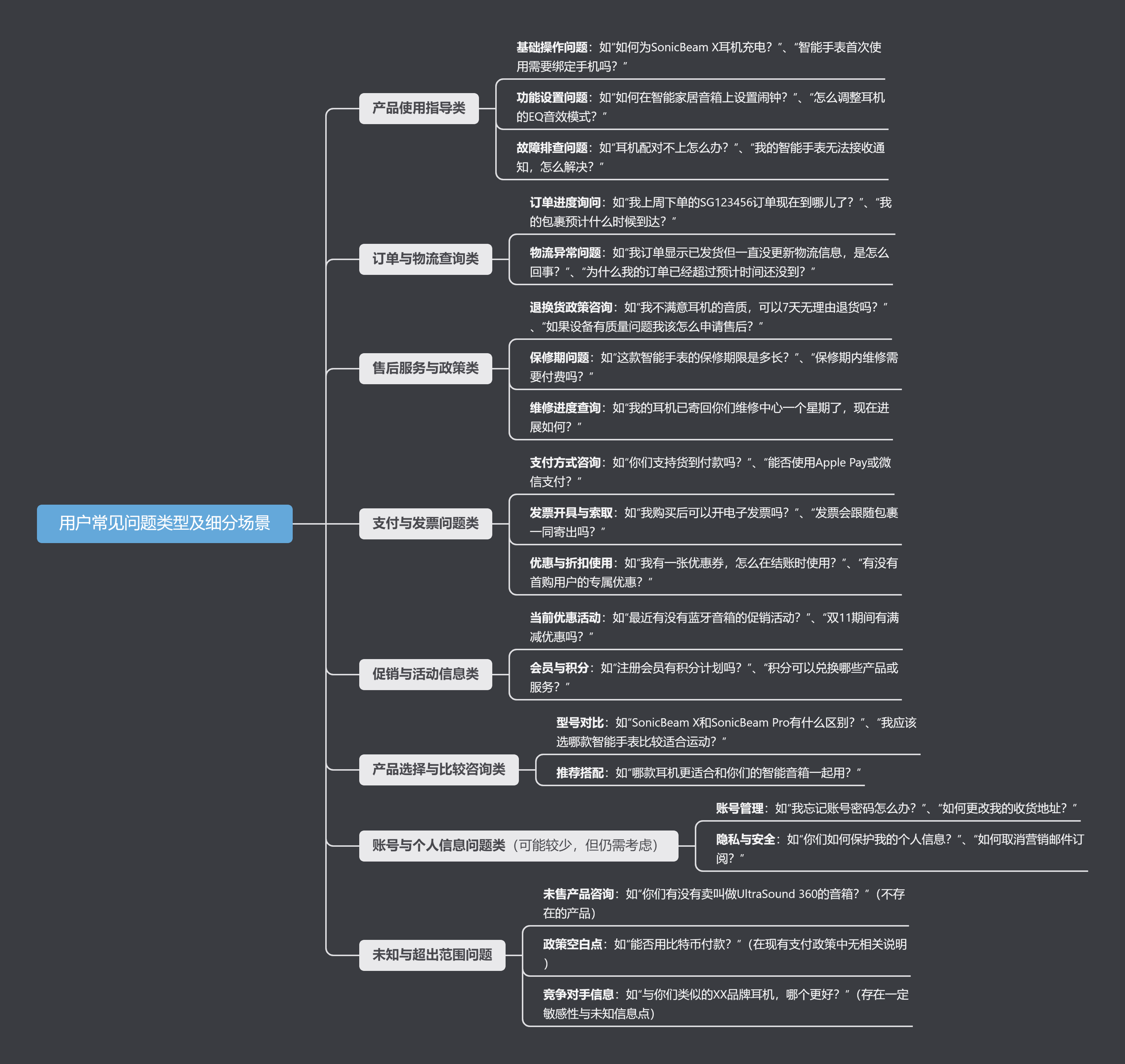
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
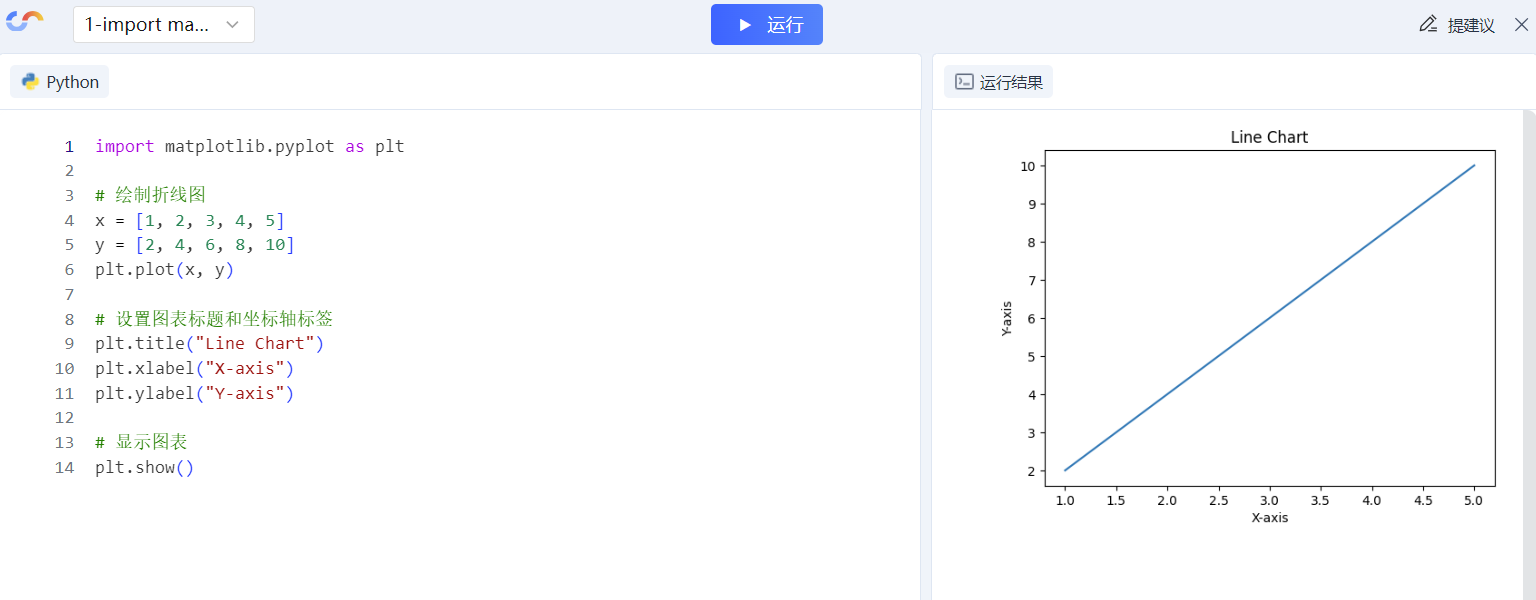
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
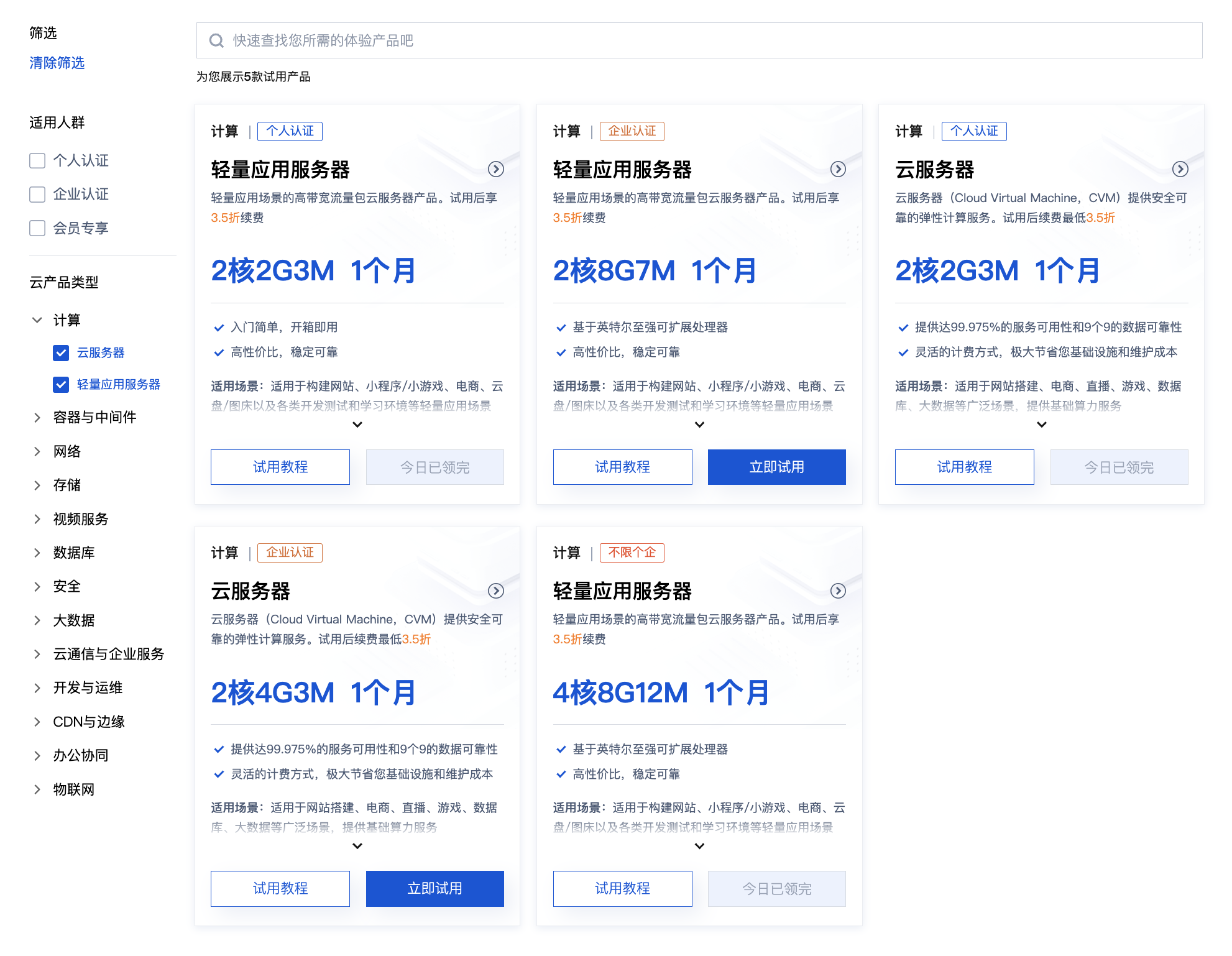
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.