Проект практической борьбы с обнаружением глубокого голоса и распознаванием подделок: полный алгоритм шумоподавления + приложение с исходным кодом Python
Предисловие
В настоящее время технология глубокого распознавания подделок голоса достигла определенного прогресса. Исследователи использовали методы машинного и глубокого обучения для разработки серии алгоритмов подделки путем анализа характеристик речевого сигнала.
Однако с постоянным развитием генеративных больших моделей и других технологий синтеза речи точность поддельной речи также постоянно улучшается, что делает задачу идентификации подделки речи все более сложной и сложной.
Эта серия статей начнется с базового хранения речевых данных и подробного анализа. Поскольку в этой серии колонок подробно объясняется содержание глубокого обучения и машинного обучения, обработки аудиоданных и современных моделей классификации речи и моделей кодирования, используемых в современных технологиях. Основное содержание серии статей этого проекта. Подробное содержание этой серии проектов представлено на рисунке ниже:
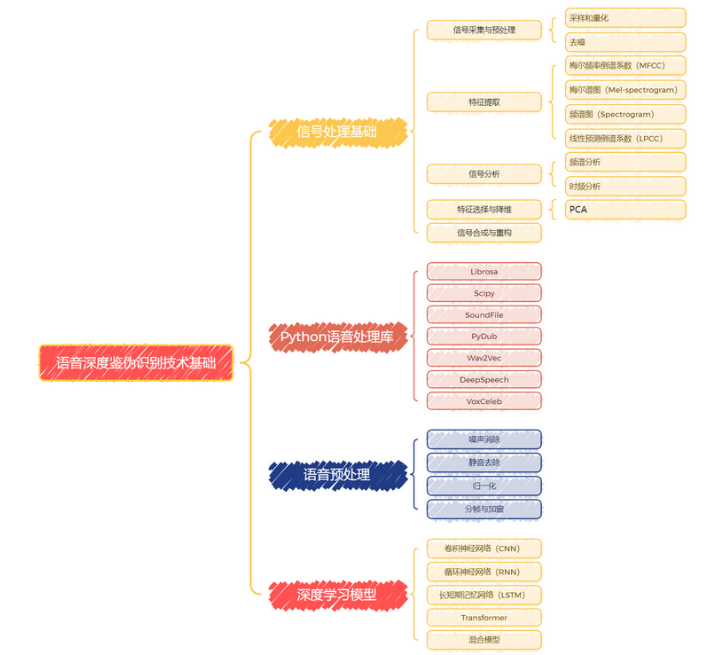
Я сделаю все возможное, чтобы все поняли и ознакомились с структурой нейронных сетей, обеспечили четкое понимание и плавные выводы, а также постараемся не использовать слишком много математических формул и профессиональных теоретических знаний. Быстро поймите и реализуйте алгоритм в одной статье и овладейте этими знаниями наиболее эффективным способом. Надеюсь, нуждающиеся друзья не пропустят рубрику, заботливо созданную автором.
В предыдущей статье были даны подробные ответы на некоторые типы и эффекты аудиошума, а также на спектральное вычитание (Spectral Вычитание) и адаптивная фильтрация (Адаптивная Фильтрация), далее нам нужно продолжить понимание Шумоподавления. вейвлет-преобразованияи Винеровский В конце фильтр выполняет алгоритм шумоподавления.
Шумоподавление вейвлет-преобразования
Вейвлет-преобразование — это метод, позволяющий одновременно анализировать сигналы во временной и частотной областях. Он использует вейвлет-функции для разложения сигналов в нескольких масштабах и может эффективно фиксировать локальные характеристики и точки мутации сигналов. В приложениях шумоподавления вейвлет-преобразование широко используется для обработки различных типов сигналов, таких как речевые сигналы, изображения, медицинские сигналы и т. д.
Подробные шаги
1. Вейвлет-разложение
Выполняя вейвлет-разложение сигнала, можно получить коэффициенты аппроксимации и коэффициенты детализации в разных масштабах.
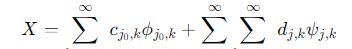
2. Пороговая обработка
Выполните пороговую обработку коэффициентов детализации, чтобы удалить шум. Распространенными методами пороговой обработки являются:
- Жесткий порог:Установите коэффициенты, меньшие порога, равными нулю。
- Мягкое пороговое значение:Установите коэффициенты, меньшие порога, равными нулю,Коэффициенты, превышающие порог, уменьшаются по определенным правилам.
Жесткая установка порога — это простой метод установки нуля, в то время как мягкая установка порога «сжимает» вейвлет-коэффициенты, превышающие порог, то есть вычитая порог, так что кривая ввода-вывода становится непрерывной. При выборе порогов люди обычно используют мягкие пороги.
Улучшенный порог представляет собой компромисс между жестким порогом и мягким порогом, то есть, когда вейвлет-коэффициент меньше порога, он не просто устанавливается на ноль, а плавно снижается до нуля. Когда он больше порога, амплитуда. вейвлет-коэффициента снижается. Перейти к порогу. Таким образом, обеспечиваются как большие вейвлет-коэффициенты, так и плавный переход коэффициентов после пороговой обработки.
Выбор порога
В процессе шумоподавления вейвлет-преобразованием решающее значение имеет выбор порога, который напрямую влияет на эффект шумоподавления. Обычно используемые методы выбора порога включают универсальный порог и адаптивный порог. Логика расчета этих двух методов подробно представлена ниже.
1. Универсальный порог
Универсальный порог — это простой и эффективный метод выбора порога, предложенный Донохо и Джонстоном. Общий порог рассчитывается следующим образом:
в:
\sigma — стандартное отклонение шума.
- Оцените стандартное отклонение шума:Обычно используются коэффициенты высокочастотной детализации.(нравиться Вейвлет-разложение Последний уровень детализации коэффициента после)Медианное абсолютное отклонение(MAD)Приходить Оцените стандартное отклонение шума。
sigma = np.median(np.abs(coeffs[-level])) / 0.6745n длина сигнала.
2. Адаптивное пороговое значение (SURE Thresholding)
Метод адаптивного порога (SURE, несмещенная оценка риска Штейна) выбирает порог путем минимизации предполагаемого риска (ошибки). Метод SURE позволяет выбирать пороговые значения отдельно для коэффициентов разных шкал, что делает его более гибким.
Рассчитайте порог для каждой шкалы:Для каждого масштабного коэффициента,Рассчитайте оптимальный порог.
Рассчитать значение SURE:РассчитайтеSUREценить,Выберите порог, который минимизирует значение SURE.
def calculate_sure_threshold(coeff):
n = len(coeff)
sorted_coeff = np.sort(np.abs(coeff))
risks = np.zeros(n)
for i in range(n):
t = sorted_coeff[i]
risk = (n - 2 * (i + 1) + np.sum(np.minimum(coeff**2, t**2))) / n
risks[i] = risk
best_threshold = sorted_coeff[np.argmin(risks)]
return best_threshold3. Вейвлет-реконструкция
Выполните обратное вейвлет-преобразование на обработанных коэффициентах, чтобы восстановить сигнал. Формула обратного преобразования противоположна формуле разложения и использует обработанные коэффициенты для восстановления сигнала.
# Вейвлет-реконструкция
denoised_signal = pywt.waverec(coeffs_thresh, wavelet)Общий код шумоподавления:
def wavelet_denoising(signal, wavelet='db1', level=1, thresholding='soft'):
# Вейвлет-разложение
coeffs = pywt.wavedec(signal, wavelet, level=level)
# Рассчитать порог
universal_threshold = calculate_universal_threshold(coeffs)
# Пороговое значение
coeffs_thresh = []
for i, c in enumerate(coeffs):
if i == 0: # Сохранять коэффициенты аппроксимации
coeffs_thresh.append(c)
else:
# использоватьSUREПороговое значение Коэффициент детализации
sure_threshold = calculate_sure_threshold(c)
if thresholding == 'hard':
coeffs_thresh.append(pywt.threshold(c, sure_threshold, mode='hard'))
elif thresholding == 'soft':
coeffs_thresh.append(pywt.threshold(c, sure_threshold, mode='soft'))
# Вейвлет-реконструкция
denoised_signal = pywt.waverec(coeffs_thresh, wavelet)
return denoised_signal
def calculate_universal_threshold(coeffs):
# Использовать коэффициент высокочастотной детализации стандартное отклонение шума
sigma = np.median(np.abs(coeffs[-1])) / 0.6745
# Вычислить общий порог
threshold = sigma * np.sqrt(2 * np.log(len(coeffs[-1])))
return threshold
def calculate_sure_threshold(coeff):
n = len(coeff)
if n == 0:
return 0
sorted_coeff = np.sort(np.abs(coeff))
risks = np.zeros(n)
for i in range(n):
t = sorted_coeff[i]
risk = (n - 2 * (i + 1) + np.sum(np.minimum(coeff**2, t**2))) / n
risks[i] = risk
best_threshold = sorted_coeff[np.argmin(risks)]
return best_threshold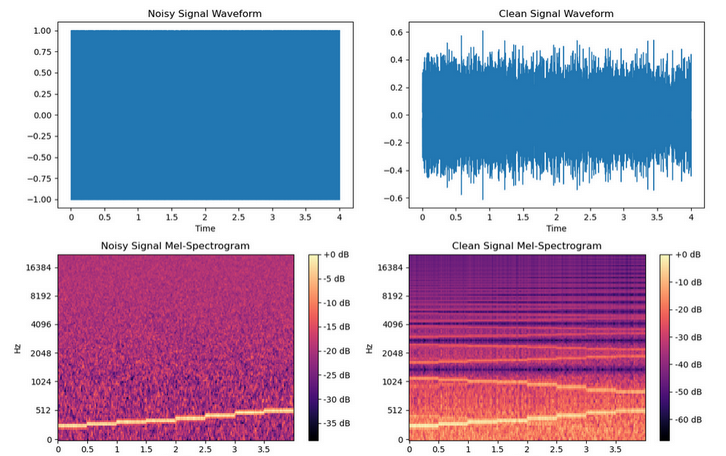
Способность шумоподавления аудиоэффекта по-прежнему средняя, и он немного чище, чем исходный звук.
Винеровский фильтр
Винеровский фильтр — метод линейной фильтрации, предложенный Норбертом Винером.,Направлен на достижение оценки сигналов с шумоподавлением путем минимизации среднеквадратической ошибки (MSE) между выходным сигналом и полезным сигналом. Фильтрация Винера может применяться как во временной, так и в частотной области.,Это классический метод в области обработки сигналов и изображений.
Основная идея фильтрации Винера заключается в использовании статистических характеристик сигнала и шума для разработки фильтра, минимизирующего среднеквадратическую ошибку между отфильтрованным выходным сигналом и полезным сигналом. Логику алгоритма можно разделить на четыре этапа:
1.Моделирование:
- Предположим, что наблюдаемый сигнал x(t) это реальный сигнал s(t) с шумом n(t) суперпозиция x(t)=s(t)+n(t) 。
- Предположим, шумn(t) представляет собой белый шум с нулевым средним и аналогичен сигналу s(t) Не связанные друг с другом.
2.Выражение частотной области:
- Преобразование сигнала в частотную область,Использование преобразования Фурье,Воля Конструкция фильтра Винера — это фильтр частотной области.
3.Конструкция фильтра Винера:
- Фильтр Винера Выражение частотной области Формула: H(f)=\frac{S_{s}(f)}{S_{s}(f)+S_{n}(f)} в,S_{s}(f) и S_{n}(f) – спектральная плотность мощности сигнала и шума соответственно.
4.Применить фильтр:
- Примените фильтр Винера к наблюдаемому сигналу, чтобы получить предполагаемый истинный сигнал.
Винеровская фильтрация в частотной области
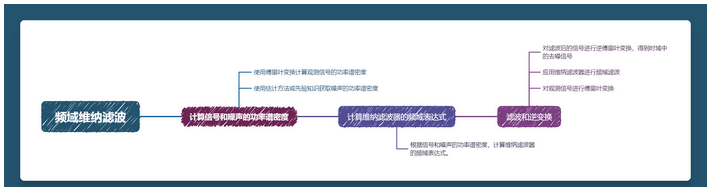
Рассчитать спектральную плотность мощности сигналов и шума:
- Вычислите спектральную плотность мощности наблюдаемого сигнала с помощью преобразования Фурье.
- Получите спектральную плотность мощности шума с помощью методов оценки или предшествующих знаний.
Рассчитать отражение фильтра Винера частотной области Режим:
- По спектральной плотности мощности сигнала и шума,Рассчитать отражение фильтра Винера частотной области Режим。
Фильтрация и обратное преобразование:
- Преобразование Фурье выполняется над наблюдаемым сигналом.
- Примените фильтр Винера для фильтрации частотной области.
- Выполните обратное преобразование Фурье на отфильтрованном сигнале, чтобы получить сигнал с шумоподавлением во временной области.
def wiener_filter(noisy_signal, sample_rate, noise_power_spectrum):
# Рассчитайте спектральную плотность мощности наблюдаемого сигнала
f, Pxx = scipy.signal.welch(noisy_signal, sample_rate, nperseg=1024)
# Оцените спектральную плотность мощности сигнала (предполагая, что сигнал шумом не зависит и спектральная плотность мощности шума известна)
signal_power_spectrum = np.maximum(Pxx - noise_power_spectrum, 1e-8)
# Рассчитать отражение фильтра Винера частотной области Режим H_wiener = signal_power_spectrum / (signal_power_spectrum + noise_power_spectrum)
# Преобразование Фурье наблюдаемого сигнала
noisy_signal_fft = np.fft.fft(noisy_signal)
# Интерполяция частотной области фильтров Винера
H_wiener_interp = np.interp(np.fft.fftfreq(len(noisy_signal)), f, H_wiener)
# Примените фильтр Винера для фильтрации в частотной области
filtered_signal_fft = noisy_signal_fft * H_wiener_interp
# Выполните обратное преобразование Фурье на отфильтрованном сигнале
filtered_signal = np.fft.ifft(filtered_signal_fft).real
return filtered_signalОбязательным условием использования этого алгоритма является расчет спектральной плотности мощности шума. Спектральная плотность мощности шума (PSD) является важным инструментом для описания распределения энергии шумовых сигналов в частотной области. В практических приложениях спектральную плотность мощности шума обычно необходимо оценивать на основе наблюдаемого шумового сигнала. Мы можем оценить спектральную плотность мощности шума с помощью адаптивных методов, статистического анализа или методов, основанных на моделях, что подходит для ситуаций, когда сигнал и шум смешиваются более сложно.
def adaPtive_noisy(file,noise_estimation_duration=1.0):
# Чтение шумных аудиофайлов
noisy_signal, sample_rate = sf.read(file)
# Рассчитайте спектральную плотность мощности зашумленных сигналов с помощью метода Уэлча.
frequencies, Pxx = scipy.signal.welch(noisy_signal, sample_rate, nperseg=10000)
# Оцените спектральную плотность мощности шума
noise_frames = int(noise_estimation_duration * sample_rate / 512)
noise_power_spectrum = np.mean(Pxx[:noise_frames])
# Визуализация спектральной плотности мощности шума
plt.figure()
plt.semilogy(frequencies, noise_power_spectrum)
plt.title('Estimated Noise Power Spectral Density')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Power Spectral Density [V^2/Hz]')
plt.show()
return noise_power_spectrumЗатем путем кодирования сначала реализуются различные алгоритмы шумоподавления. Позже мы можем выполнять небольшие приложения с различными эффектами шумоподавления в соответствии с различными бизнес-сценариями и потребностями, а также использовать их для прямой трансляции аудио и видео или для шумоподавления голоса в реальном времени. эффекты. Итак, в следующей главе мы начнем изучать наиболее важные особенности аудио и соответствующие им значения, как нам следует использовать эти функции и как видеть сквозь WAV-данные эти функции.
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
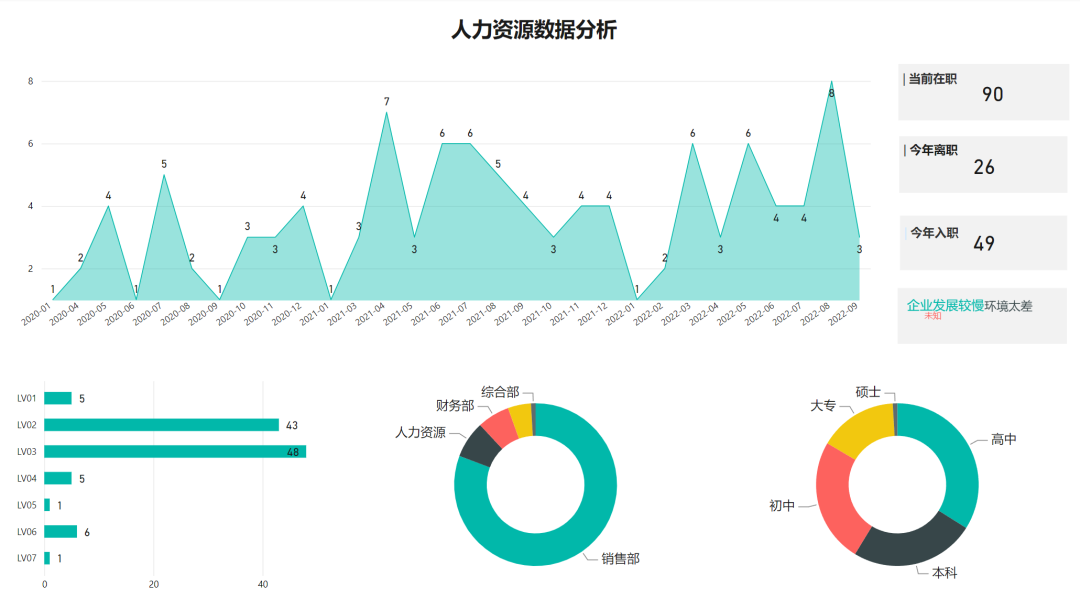
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
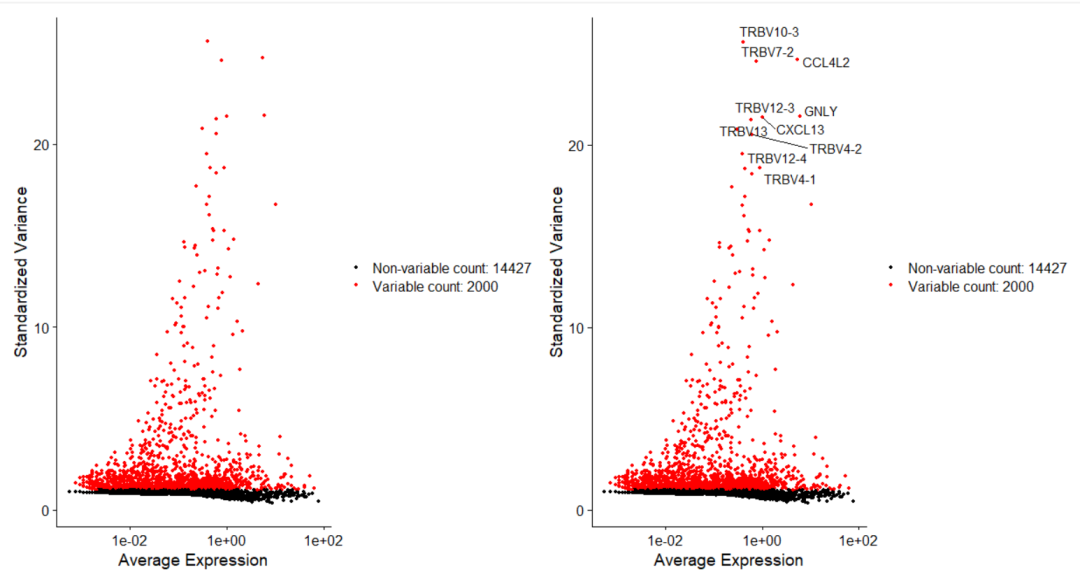
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
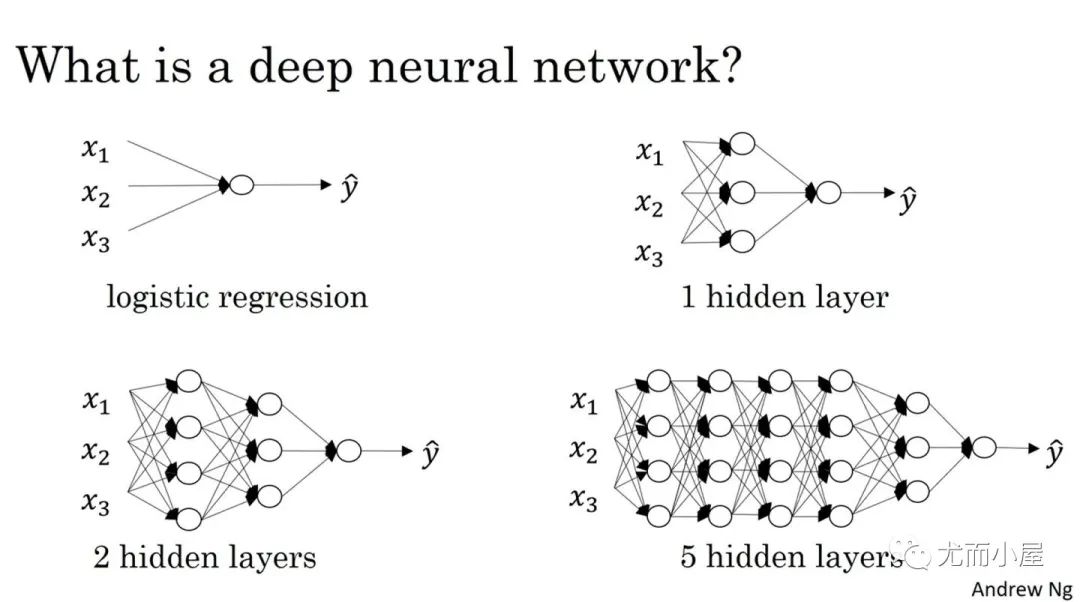
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


