Подробное введение и алгоритм вывода регрессии опорных векторов (SVR)
Всем привет, мы снова встретились, я ваш друг Цюаньчжаньцзюнь.
1 SVRфон
2 Принцип СВР
3 Математическая модель СВР
- Фон СВР СВР был предложен как ответвление СВМ. На рисунке показана связь между СВР и СВМ.

Геометрический интервал между двумя пунктирными линиями здесь равен r = d ∣ ∣ W ∣ ∣ \frac{d}{||W||} ∣∣W∣∣d, где d — функциональный интервал между двумя пунктирными линиями. (Одна картинка для понимания функциональных интервалов и геометрических интервалов)

Здесь r рассчитывается на основе формулы расстояния между двумя параллельными линиями.

- Принцип СВР
Разница между УВО и общей линейной регрессией
SVR | общая линейная регрессия |
|---|---|
1. Если данные находятся в пределах диапазона интервалов, потери не будут рассчитываться тогда и только тогда, когда абсолютное значение разницы между f(x) и y больше, чем ϵ \epsilon ϵ. | 1. Рассчитайте потери, пока f(x) не равна y. |
2. Оптимизируйте модель, максимизируя ширину интервала и минимизируя общие потери. | 2. Оптимизируйте модель путем усреднения после градиентного спуска. |

Принцип: SVR создает «интервальную зону» по обе стороны от линейной функции с интервалом ϵ \epsilon ϵ (также называемое отклонением допуска, которое представляет собой эмпирическое значение, устанавливаемое вручную. Все образцы, попадающие в интервальную зону, не затрагиваются). Рассчитайте потери, то есть только вектор поддержки будет влиять на его функциональную модель, и, наконец, оптимизированная модель получается путем минимизации общих потерь и максимизации интервала.
Примечание. Вот введение в значение опорного вектора: Интуитивно понятное объяснение: опорный вектор — это выражение конечного w.,bРасчет играет роль в образце(a>0)
Как показано на рисунке ниже, Выборки в «конвейере» соответствуют a=0, который не является опорным вектором; роды“стенка трубы”вектор опоры границы,0<a< ϵ \epsilon ϵ роды”трубопровод”Те, что снаружи, являются неграничными опорными векторами.,a> ϵ \epsilon ϵ (при обнаружении аномалий часто выбираются аномальные точки из неграничных опорных векторов)

- Математическая модель СВР
3.1 Линейная жесткая маржа SVR


3.2 Линейный мягкий запас SVR Причина: в реальных задачах часто бывает трудно напрямую определить подходящее ϵ \epsilon ϵ, чтобы гарантировать, что большая часть данных может находиться в интервале интервала, и SVR надеется, что все обучающие данные будут находиться в пределах интервала интервала, поэтому резерв добавляется переменная ξ \xi ξ, тем самым ослабляя требования к интервалу функции, то есть позволяя некоторым выборкам находиться за пределами диапазона интервалов.

После введения слабых переменных в это время все выборочные данные соответствуют условиям:

Это условие ограничения после отображения слабой переменной, поэтому его также называют — Soft Margin SVR.
Примечание. Для любого образца xi, если он находится внутри зоны изоляции или на ее границе, ξ \xi ξ все 0 выше зоны изоляции, они есть; ξ > 0 , ξ ∗ = 0 \xi>0,\xi^*=0 ξ>0,ξ∗=0 Под изоляционным поясом находится ξ ∗ > 0 , ξ = 0 \xi^*>0,\xi=0 ξ∗>0,ξ=0


Вывод параметра: Метод множителей Лагранжа (может превратить ограничения в уравнения без ограничений)
Пусть u i ⩾ 0 , u i ∗ ⩾ 0 , a i ⩾ 0 , a i ∗ ⩾ 0 u_i\geqslant0,u^*_i\geqslant0,a_i\geqslant0,a^*_i\geqslant0 ui⩾0, ui∗⩾0, ai⩾0, ai∗⩾0 — коэффициенты Лагранжа Построим функцию Лагранжа:

3.3 Нелинейность (отображение, функция ядра)

Вдохновение: увеличьте размерность, сопоставьте низкие размеры с большими (нелинейными с линейными).
Предыдущая низкоразмерная модель данных SVR появилась в виде внутреннего продукта xi*xj:

Это определяет низкоодельное до высокого уровня картирования φ \ varphi φ: для замены предыдущей формы внутреннего накопления:


Представляет внутренний продукт после сопоставления с многомерным пространством признаков.
Сопоставление с многомерными задачами: 2 измерения могут быть сопоставлены с 5 измерениями Но когда низкое измерение равно 1000, отображается в сверхвысоком измерении, внутренний продукт компьютера имеет характеристики В это время количество операций от низкой размерности к высокой увеличится взрывным образом.
Поскольку размерность пространства признаков может быть очень высокой или даже бесконечной, прямой расчет Φ ( x i ) T Φ ( x j ) \varPhi(x_i)^T\varPhi(x_j) Φ(xi)TΦ(xj) обычно сложно, здесь нам нужно спроектировать функцию ядра

Результаты показывают, что: результат вычисления функции ядра в низком измерении такой же, как результат внутреннего продукта после преобразования в высокое измерение.
Основные изменения: нелинейное преобразование, в основном путем изменения пространства внутреннего продукта и замены его другим пространством функций ядра, тем самым преобразуя его в другое линейное пространство.

Грандиозный внешний вид функции ядра: функция ядра является расширением пространства векторных внутренних произведений, так что задачу нелинейной регрессии можно превратить в приближенную задачу линейной регрессии после преобразования функцией ядра.


- Практические случаи
Обновление поколения. . . . . . .
Издатель: Лидер стека программистов полного стека, укажите источник для перепечатки: https://javaforall.cn/134863.html Исходная ссылка: https://javaforall.cn
RasaGpt — платформа чат-ботов на основе Rasa и LLM.

Nomic Embed: воспроизводимая модель внедрения SOTA с открытым исходным кодом.

Улучшение YOLOv8: EMA основана на эффективном многомасштабном внимании, основанном на межпространственном обучении, и эффект лучше, чем у ECA, CBAM и CA. Малые цели имеют очевидные преимущества | ICASSP2023
Урок 1 серии Libtorch: Тензорная библиотека Silky C++

Руководство по локальному развертыванию Stable Diffusion: подробные шаги и анализ распространенных проблем
Полностью автоматический инструмент для работы с видео в один клик: VideoLingo

Улучшения оптимизации RT-DETR: облегченные улучшения магистрали | Support Paddle облегченный rtdetr-r18, rtdetr-r34, rtdetr-r50, rtdet
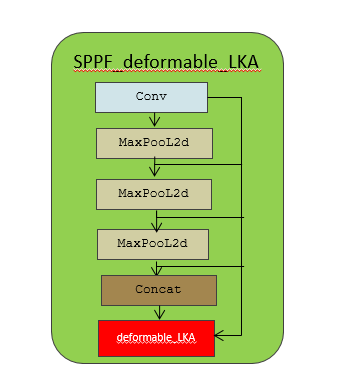
Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | Деформируемое внимание с большим ядром (D-LKA Attention), большое ядро свертки улучшает механизм внимания восприимчивых полей с различными функциями

Создано Datawhale: выпущено «Руководство по тонкой настройке развертывания большой модели GLM-4»!
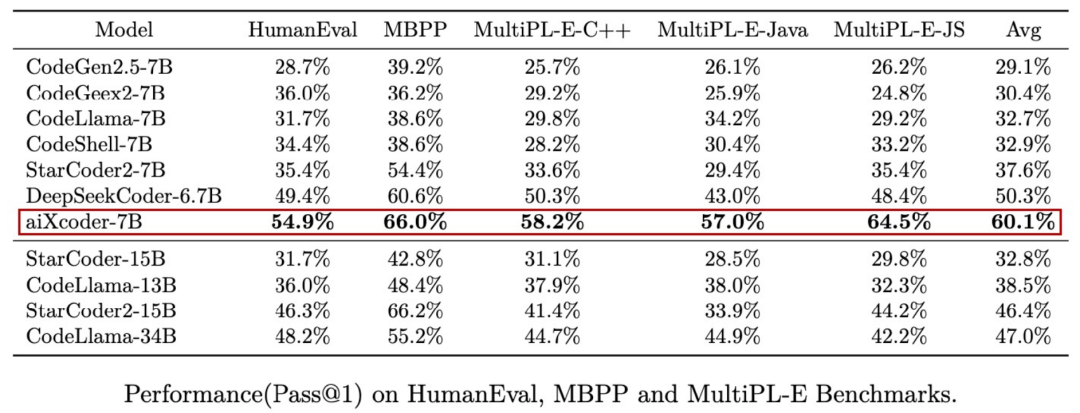
7B превышает десятки миллиардов, aiXcoder-7B с открытым исходным кодом Пекинского университета — это самая мощная модель большого кода, лучший выбор для корпоративного развертывания.
Используйте модель Huggingface, чтобы заменить интерфейс внедрения OpenAI в китайской среде.

Оригинальные улучшения YOLOv8: несколько новых улучшений | Сохранение исходной информации — алгоритм отделяемой по глубине свертки (MDSConv) |
Второй пилот облачной разработки | Быстро поиграйте со средствами разработки на базе искусственного интеллекта
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция с нулевым кодированием и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.

Решенная Ошибка | Загрузка PyTorch медленная: TimeoutError: [Errno 110] При загрузке факела истекло время ожидания — Cat Head Tiger

Brother OCR, библиотека с открытым исходным кодом для Python, которая распознает коды проверки.

Новейшее подробное руководство по загрузке и использованию последней демонстрационной версии набора данных COCO.

Выпущен отчет о крупной модели финансовой отрасли за 2023 год | Полный текст включен в загрузку |
Обычные компьютеры также могут работать с большими моделями, и вы можете получить личного помощника с искусственным интеллектом за три шага | Руководство для начинающих по локальному развертыванию LLaMA-3
Одной статьи достаточно для анализа фактора транскрипции SCENIC на Python (4)
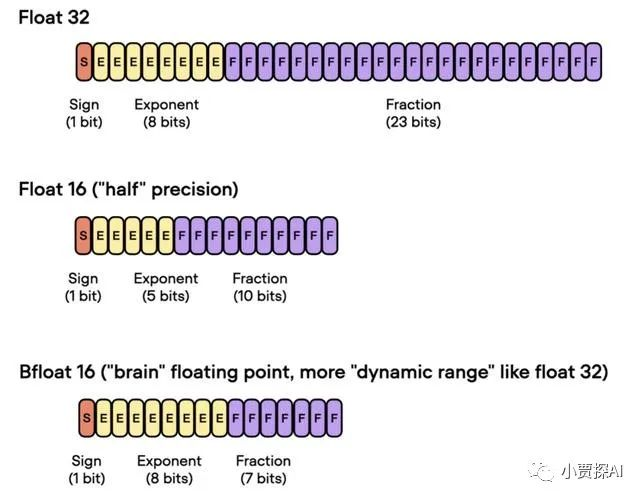
Бросая вызов ограничениям производительности небольших видеокарт, он научит вас запускать большие модели глубокого обучения с ограниченными ресурсами, а также предоставит полное руководство по оценке и эффективному использованию памяти графического процессора!

Команда Fudan NLP опубликовала 80-страничный обзор крупномасштабных модельных агентов, в котором в одной статье представлен обзор текущего состояния и будущего агентов ИИ.

[Эксклюзив] Вы должны знать о новой функции JetBrains 2024.1 «Полнострочное завершение кода», чтобы решить вашу путаницу!

Краткое изложение базовых знаний о регистрации изображений 1.0

Новейшее подробное руководство по установке и использованию библиотеки cv2 (OpenCV, opencv-python) в Python.
Легко создайте локальную базу знаний для крупных моделей на основе Ollama+AnythingLLM.
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание решения. Повторная попытка с помощью файла (графическое руководство).

Одна статья поможет вам понять RAG (Retrival Enhanced Generation) | Введение в концепцию и теорию + практику работы с кодом (включая исходный код).
Эволюция архитектуры шлюза облачной разработки

