Перевернутый маятник: моделирование Simulink [легко понять]
Всем привет, мы снова встретились, я ваш друг Цюаньчжаньцзюнь.
Перевернутый маятник: моделирование Simulink
содержание
На этой странице мы расскажем, как смоделировать систему перевернутого маятника и смоделировать тормоза с помощью Simulink и его аксессуаров. Затем нелинейное моделирование можно использовать для проверки эффективности линеаризованной версии модели. Имитационные модели также можно использовать для оценки эффективности схем управления, разработанных на основе линеаризованных моделей.
Физическая установка и системные уравнения
В этом примере мы рассмотрим двухмерную версию перевернутой маятниковой системы с тележкой, в которой размещение ограничено перемещением в вертикальной плоскости, как показано на рисунке ниже. Для этой системы управляющий вход

Сила, перемещающая тележку по горизонтали, выход — угловое положение маятника.

и горизонтальное положение тележки

。

В этом примере мы принимаем следующие величины:
(М) Масса тележки 0,5 кг
(м) Масса маятника 0,2 кг
(б) Тележка имеет коэффициент трения 0,1 Н/м/сек.
(l) Длина до центра масс маятника равна 0,3 м.
(I) Момент инерции массы маятника равен 0,006 кг·м^2.
(F) Сила, действующая на тележку
(x) Координаты положения тележки
Вертикальный (вниз) (θ) угол поворота
Ниже приведены две бесплатные схемы этой системы.

Эту систему сложно моделировать в Simulink из-за физических ограничений (штифтовых соединений) между тележкой и маятником, которые уменьшают степени свободы системы. И тележка, и маятник имеют одну степень свободы (соответственно

Придаточное предложение:

). Модифицируем второй закон Ньютона (

) генерирует дифференциальные уравнения для этих степеней свободы следующим образом.
(1)

(2)

Однако необходимо учитывать силы взаимодействия

а также

Силы взаимодействия между тележкой и маятником для полного моделирования динамики системы. Добавление этих сил требует моделирования.

-и

Масса центральных поступательных компонентов маятника дополняет его вращательные динамические свойства. существовать" Перевернутый маятник: системное моделирование» В учебнике сила взаимодействия

и

Было выполнено алгебраическое решение.
Обычно мы хотим воспользоваться Возможности моделирования Simulink делают алгебру за нас. Поэтому добавим к маятнику

-и-

Моделирование уравнений компонентов показано ниже.
(3)

(4)

(5)

(6)

Однако координаты местоположения

и

это точная функция

. Поэтому мы можем выразить их производные через

. Решите сначала

-компонентное уравнение, получаем следующие результаты.
(7)

(8)

(9)

затем обработать

-компонентное уравнение, получаем следующие результаты.
(10)

(11)

(12)

Эти выражения затем можно подставить в выражение

и

Ниже сверху.
(13)

(14)

Теперь мы можем представить эти уравнения в Simulink. Simulink можно использовать напрямую с нелинейными уравнениями, поэтому нет необходимости использовать Перевернутый маятник: системное моделирование» Линеаризуйте эти уравнения, как показано на странице.
Используйте Simulink для построения нелинейных моделей
Мы можем выполнить шаги, приведенные ниже, и использовать полученную выше формулу для построения модели перевернутого маятника в Simulink.
- Сначала введите в командном окне MATLAB середина. simulink чтобы открыть среду Simulink. Затем откройте Стартовая страница Симулинка 窗口серединавыбирать" Новый”>“ Simulink”>“пустая модель” или нажмите Ctrl-N, Откройте новое окно модели в Simulinkсередина.
- Измените тег каждого блока Fcn, чтобы он соответствовал связанной с ним функции.
- Дважды щелкните каждый блок Интегратора, чтобы добавить соответствующие переменные состояния. State Name :. Пример смотрите на изображении ниже. Также " «Начальные условия» Изменить на : “

Угол маятника равен «пи», что означает, что маятник начинает указывать прямо вверх.

- Из Симулинка / Signal Библиотека маршрутизации середина вставляет четыре блока мультиплексора (Mux), по одному на каждый блок Fcn.
- Соответственно Симулинка / SinksиSimulink / Библиотека исходного кода середина вставляет два блока Out1 и один блок In1. Затем дважды щелкните по тегу блока, чтобы изменить его имя. Два выхода предназначены для тележки из «Расположения» и маятника из «угля», а один вход — для силы, приложенной к тележке из «силы».
- Подключите каждый выход блока Mux к соответствующему входу блока Fcn.

Теперь вводим четыре уравнения (1), (2), (13) и (14) в блок Fcn середина соответственно. Давайте начнем с повторения уравнения (1) ниже.
(15)

- Подключите эти три входа к этому блоку Mux в порядке, указанном на предыдущем шаге.
- Дважды щелкните первый блок Fcn и введите xddot из уравнения, как показано ниже.

Теперь введем уравнение (2), которое будет повторено ниже.
(16)

- Введите приведенное выше уравнение в блок Fcn середина, измените входную величину блока Mux, а затем подключите правильные сигналы к блоку Mux в правильном порядке.
- Повторите этот процесс для уравнений (13) и (14) ниже.
(17)

(18)

После выполнения всех этих шагов полученная модель должна выглядеть следующим образом.

Чтобы сохранить все эти компоненты как один блок подсистемы, сначала выберите все блоки, затем щелкните правой кнопкой мыши по выделению и выберите выбирать" из выбора Создать подсистему" . Ваша модель должна выглядеть так. Вы также можете щелкнуть правой кнопкой мыши здесь ,Затемвыбирать" Сохранить ссылку как…» для загрузки системных файлов.

Построение нелинейных моделей с использованием Simscape
В этом разделе мы также покажем, как построить модель перевернутого маятника, используя модуль физического моделирования расширения Simscape Simulink. Блоки в библиотеке Simscape представляют собой реальные физические компоненты, поэтому сложные модели динамики множества тел можно строить без необходимости построения математических уравнений, основанных на физических принципах, как это было сделано выше, путем применения законов Ньютона.
Откройте новую модель Simulink и выполните следующие действия, чтобы создать модель перевернутого маятника в Simscape. Для ориентирования примем систему координат, в которой движется автомобиль –

направление (положительное вправо

направление) движется, а положительное – направление вверх. Согласно стандартной практике,

Затем укажите положительное направление на плоскость движения.
- Из Симскейп / Multibody / First Generation(1G)/ Библиотека Bodies середина вставляет блок Body, представляющий корзину покупок. Следуйте системным параметрам, указанным вверху этой страницы, дважды щелкните блок и поместите качество: установить на " 0,5 дюйма в единицах kg . По умолчанию блок Body включает в себя два порта. Так как нам нужны порты для определения маятника для соединения с тележкой Расположение Также действует внешняя сила и трение и з Расположение, поэтому необходимо добавить третий порт. Это можно сделать через " Расположение"Правая часть вкладкиизкнопка готова。Поскольку тележка может двигаться только в одном измерении.,Следовательно, две силы должны быть сосредоточены вдоль этого измерения (

-направление). Поскольку мы, по сути, моделируем корзину покупок как точечную массу, которую можно только транслировать, вам не нужно изменять какие-либо другие параметры по умолчанию. Однако мы планируем использовать Simscape для анимации движения системы, поэтому относительно ее центра тяжести будут созданы дополнительные порты (CG ) определяет четыре угла корзины для покупок (только 2D). На изображении ниже показано возможное определение корпуса тележки.

- Вставьте второй блок Body, чтобы представить маятник. Дважды щелкните блок и поместите качество: установить на " 0,2 дюйма, единица измерения кг. Поскольку маятник может только вращаться -

вращение оси,Поэтому необходимо лишь определить инерцию, связанную с этим основным направлением. для простоты,определениеИнерция: равный" 0.006 * глаз(3)", единица измерения kg * m ^ 2 . Поскольку мы моделируем маятник как твердое тело с большой и малой массой, то это тело может вращаться, поэтому важно правильно определить место крепления маятника к тележке и его центральную точку. В частности, определите точки соединения CS1 Позиция [[0 0 0]", а начало координат соседний и будет CG определяется как привязанность CS1 (как определено выше) на расстоянии 0,3 метра друг от друга. Также определите четыре угла маятника. Убедитесь, что порт, определяющий точку подключения, отображается. существовать" Визуализация" На вкладке «Маятник» вы также можете изменить цвет маятника, чтобы он выделялся среди корзины покупок.

- Далее, Из Симскейп / Multibody / First Generation(1G)/ Библиотека Jjoints середина добавляет блок Revolute для определения соединения, соединяющего маятник с тележкой. По умолчанию суставы будут определены вокруг:

Вращайтесь по оси, соответствующей ситуации, которую мы моделируем. Подсоедините кузовной модуль, соответствующий тележке, к базовому порту шарнира (B ), подключите корпусной модуль, соответствующий маятнику, к ведомому порту шарнира ( F ). двойной щелчок" Блок Revolute и замените " Количество портов датчика/исполнительного устройства: "Установить" 2”。
- Тогда Из Симскейп / Multibody / First Generation(1G)/ Библиотека датчиков и исполнительных устройств серединадобавить соединение Initial Блок условий и сустав Сенсорные блоки и подключите эти блоки к блокам Revolute. Дважды щелкните на «United» «Начальные условия» и выберите «середина» Давать возможность"коробка。Мы можем использовать значения по умолчанию для суставовизисходный Расположениеискорость。использовать0степеньизисходный Расположениесоответствует вышеуказанномуиз Маятникизопределение垂直向上指向изпомещать。Это связано сиз原始определение不一致

, но это приведет к тому, что результаты ответов будут соответствовать результатам других страниц в этом примере середина Генерация результатов на основе линеаризованной модели. Далее дважды кликните по блоку «Joint Sensor», Тогда меняй»угол" Единица измерения изменится на rad . Угловое положение — единственное измерение, необходимое для этого соединения, остальные поля можно оставить неустановленными.
- Из Симскейп / Multibody / First Generation(1G)/ Библиотека соединений середина добавляет два призматических блока для определения тележки с поступательными степенями свободы. также оказывает давление на тележку. Поскольку тележка технически представляет собой точечную массу, нам нужен только один призматический блок, но, используя два призматических блока, мы можем применять силу в разных местах Расположения. Дважды щелкните по каждому блоку призмы. Тогда меняй» «Ось действия»Изменить на“ [1 0 0]", чтобы отразить две силы -

Тот факт, что направление работает. Затем подключите подчиненный порт каждого модуля (F ) подключается к кузовному модулю, представляющему собой тележку, для приложения силы ( CS1 ) и сила трения ( CS2 ) порт.
- Далее, Из Симскейп / Multibody / First Generation(1G)/ Библиотека тел середина добавляет два блока Ground для определения основы движения тележки. В частности, подключите каждый заземляющий блок выхода к каждому призматическому блоку базового порта ( B )。
- Для одного из только что созданных наземных блоков дважды щелкните его и выберите середина. Порт «Показать машинную среду»коробка。Тогда Из Симскейп / Multibody / First Generation(1G)/ Библиотека тел середина добавляет Машину Environment и подключите его к порту, который вы только что добавили из модуля Ground. Модуль Machine Environment позволяет нам определять гравитацию в моделировании. в этом случае

,m / s ^ 2 Единица измерения по умолчанию (отрицательное направление) и размер (" 9.81") верно. Этот блок также позволяет нам определить параметры визуализации и числового решателя. Для этого примера подходят параметры по умолчанию.
- Далее, Из Симскейп / Multibody / First Generation(1G)/ Библиотека датчиков и исполнительных механизмов середина добавляет два модуля совместных исполнительных устройств и один модуль совместных датчиков. Модуль привода суставов будет использоваться для создания внешней силы и трения, а модуль датчиков суставов будет определять движение автомобиля. Обратите внимание, что доступен также блок поступательного трения, но поскольку мы работаем только с простой вязкой моделью, мы рассчитаем трение самостоятельно. Дважды щелкните один из блоков «Призма» и измените « Количество портов датчика/исполнительного устройства: "Установить" 1" (для силовых приводов). Для остальных призматических блоков установите Количество портов датчика/исполнительного устройства: приезжать" 2” (один для силового привода, а другой для датчика тележки). Затем подключите шарнирный привод и модуль шарнирного датчика, как описано. В этом случае достаточно стандартного модуля шарнирного привода, но из-за расчета трение требует скорости. поэтому надо поставить модуль совместного датчика Изменить на выходе Расположениеискорость. Дважды щелкните модуль «Датчик сустава» и выберите «середина». скорость "поле, также выберите середина" Расположение ” Нет необходимости менять единицы измерения по умолчанию. Также снимем флажок “середина”. Выбранный параметр выводится в виде сигнала флажок.
- Из Симулинка / Math Библиотека операций середина добавляет блок усиления для представления коэффициента вязкого трения.

. Измените «Усиление «Установить», как указано вверху страницы. 0,1 дюйма и подключите вход к выходу скорости модуля датчика шарнира автомобиля и подключите выход усиления к приводу фрикционного шарнира.
- Далее, Из Симулинка / Библиотека портов и подсистем середина добавляет два блока Out1 и один блок In1. Подключите модуль Out1 к оставшимся из совместных выходов модуля датчиков, а модуль In1 — к оставшимся из совместных входам исполнительного механизма.
- Наконец, соедините и пометьте компоненты, как показано на рисунке ниже. Вы можете поступить аналогичным образом с переворачиванием вращающихся блоков. блок, т.е. щелкните правой кнопкой мыши по блоку и выберите из " Поворот и переворот» менюсерединавыбирать" вращающийся блок ” 。

Вы также можете сохранить модель как отдельные блоки подсистемы, как описано в предыдущем разделе. Вы можете щелкнуть правой кнопкой блок мыши и серединавыбирать» из меню результатов цвет фона" изменить подсистему цвет . Вы можете щелкнуть правой кнопкой мыши здесь Загрузите полный файл модели, но учтите, что вам нужна надстройка Simscape для Simulink, чтобы запустить файл. Мы находимся в " Перевернутый маятник: проектирование контроллера Simulink» Используйте эту модель на странице 。
создать ответ разомкнутого цикла
Теперь мы смоделируем реакцию перевернутой маятниковой системы на силу удара, приложенную к тележке. Эта симуляция требует импульсного ввода. Поскольку в библиотеке Simulink такого блока нет, мы будем использовать блок Pulse Generator для аппроксимации входного единичного импульса. Мы можем использовать любую из созданных выше моделей, однако в данном случае мы будем использовать модель Simscape, поскольку она позволяет нам визуализировать движение перевернутой маятниковой системы. Пожалуйста, следуйте инструкциям ниже.
- Откройте симскейп-модель перевернутого маятника, созданную выше.
- Из Симулинка / Библиотека исходников серединадобавить Pulse Генераторный модуль. Дважды щелкните по блоку и измените параметры, как показано ниже. В частности, " период: ”Изменить на“ 10". Поскольку мы будем запускать симуляцию в течение 10 секунд, мы можем гарантировать, что генерируется только один "импульс". Также добавьте Амплитуда Изменить на“ 1000" и будет Ширина импульса (в процентах от периода) Изменить на“ 0,01". Вместе эти настройки дают примерно единицу импульса из импульса, и поскольку входная величина Амплитуда очень велика в течение короткого времени, площадь импульса равна 1.

- Из Симулинка / Библиотека стоков середина добавляет блок диапазона.
- Для того, чтобы отобразить на осциллографе оба входа, щелкните правой кнопкой мыши по блоку «Осциллограф», выбор» Сигнал и Порт", Тогда меняй» Введите количество портов ”Изменить на“ 2”。
Подключите модули, как показано, и промаркируйте сигналы, подключенные к модулю осциллографа.

Сохраните эту систему как Pend_Openloop.slx или щелкните правой кнопкой мыши. здесь ивыбирать" Сохранить ссылку как…» Скачать 。
Прежде чем начать моделирование, нам необходимо включить визуализацию системы перевернутого маятника. В верхней части окна модели из менюсередина выберите" моделирование”>“Параметры конфигурации модели” . Затем выберите из каталога в левой части окна Simscape Multibody 1G . Затем выберите Процесс моделирования середина показать анимацию коробку, как показано ниже.

Теперь запустите симуляцию (с " симуляция" Меню выбора середина "бегать" или введите Ctrl-T )。существовать Процесс В представлении середина, перевернутый маятник анимации (как показано ниже) визуализирует систему, производящую движение.

Затем откройте прицел. Вы увидите следующий вывод об угле поворота и расположении тележки.

Обратите внимание, что маятник несколько раз совершает полный оборот, причем его угол середина

Переворот дуги. Кроме того, положение тележки неограниченно увеличивается, но колеблется под действием качающегося маятника. Эти результаты согласуются с « Перевернутый маятник: системный анализ» страницасерединапоказыватьиз开环моделирование结果相差很大。конечно,Это связано с тем, что при моделировании используется полностью нелинейная модель.,Однако предыдущий анализ опирался на линейную аппроксимацию модели перевернутого маятника. Более непосредственное сравнение результатов имитационной модели с предыдущими результатами.,Мы извлечем линейную модель из имитационной модели середина.
Извлечение линейных моделей из моделирования
Помимо сравнения нашей имитационной модели с предыдущими результатами, может возникнуть необходимость извлечь линейную модель для целей анализа и проектирования. Обычно применяется к анализу динамических систем и связанному с ними проектированию средств управления. Многие методы анализа можно применять только к линейным моделям. Следовательно, можно ожидать, что из нелинейной имитационной модели будет извлечена приблизительно линейная модель. Мы сделаем это в Simulinkсередина.
- Сначала откройте одну из моделей Simulink, созданных выше, Pend_Model.slx или Pend_Model_Simscape.slx.
- Если имитационная модель создается с использованием переменных, физические константы должны быть определены в рабочем пространстве MATLAB середина перед выполнением линеаризации. Это можно сделать, введя следующую команду в командном окне MATLAB середина.
M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;
- Далее выберите меню «серединавыбирать» вверху окна модели. анализировать”>“конструкция управления”>“«Линейный анализ» . Это приведет к Инструменты линейного анализа Окно открывается.
- Чтобы выполнить линеаризацию, нам сначала нужно определить модель входов и выходов. Также мы хотим линеаризовать его из рабочей точки. Сначала щелкните правой кнопкой мыши представителя Simulink. / Модель Simscape является серединой «принудительного» ввода сигнала. Затем из меню результатовсерединавыбрать" 线性анализировать点”>“开环输入 ". Аналогично щелкните правой кнопкой мыши по каждому из двух выходных сигналов модели из (угол поворота и положение тележки) серединаиз и в каждом случае из меню результатов серединавыбирать" 线性анализировать点”>“开环输出 «Окончательные входы и выходы теперь должны быть обозначены на модели символами стрелок, как показано на рисунке ниже.

- Далее нам нужно определить рабочую точку, которую нужно линеаризовать. от" Рабочая точка:" менюсередина,выбирать" Модель чернослива" , как показано на рисунке ниже. Это откроется" Модель чернослива" окно. В этом окне середина выберите индикатор зеленого треугольника из Начать обрезку кнопка. Это создаст рабочую точку op_trim1 。
- Поскольку мы хотим изучить импульсную характеристику этой системы, пожалуйста, верните " «Линейный анализ» вкладка и выбор" пульс" , как показано на рисунке ниже.

- Наконец, из " Рабочая точка:" Перетащите в меню выбора середина op_trim1 , а затем представлен маленьким зеленым треугольником из" пульс" кнопка. Это автоматически сгенерирует график импульсной характеристики и линеаризованную модель. linsys1 。
- Чтобы сравнить результаты с " Перевернутый маятник: системный анализ» Страница середина генерируется из диаграммы для сравнения, необходимы изменения -

Масштабирование оси. Это можно сделать через контекстное меню серединавыбирать" свойство" добиться. Затем должно появиться окно из, как показано ниже, изображение выше — это реакция угла поворота из, а изображение ниже — реакция тележки «Расположение».

Эти фотографии связаны с « Перевернутый маятник: системный анализ» Страница середина генерирует диаграммы, которые очень похожи, но не идентичны.
Мы также можем экспортировать полученную линеаризованную модель в Рабочее пространство MATLAB для дальнейшего анализа и проектирования. Только что Рабочая область линейного анализасередина из linsys1 Нажмите на объект мышь Это можно сделать, щелкнув правой кнопкой мыши, чтобы скопировать объект. затем в Рабочее пространство MATLABсередина Нажмите «Объект как объект».
Издатель: Лидер стека программистов полного стека, укажите источник для перепечатки: https://javaforall.cn/171016.html Исходная ссылка: https://javaforall.cn

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
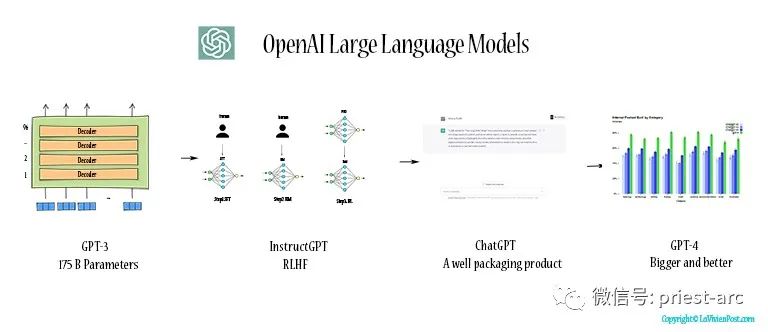
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

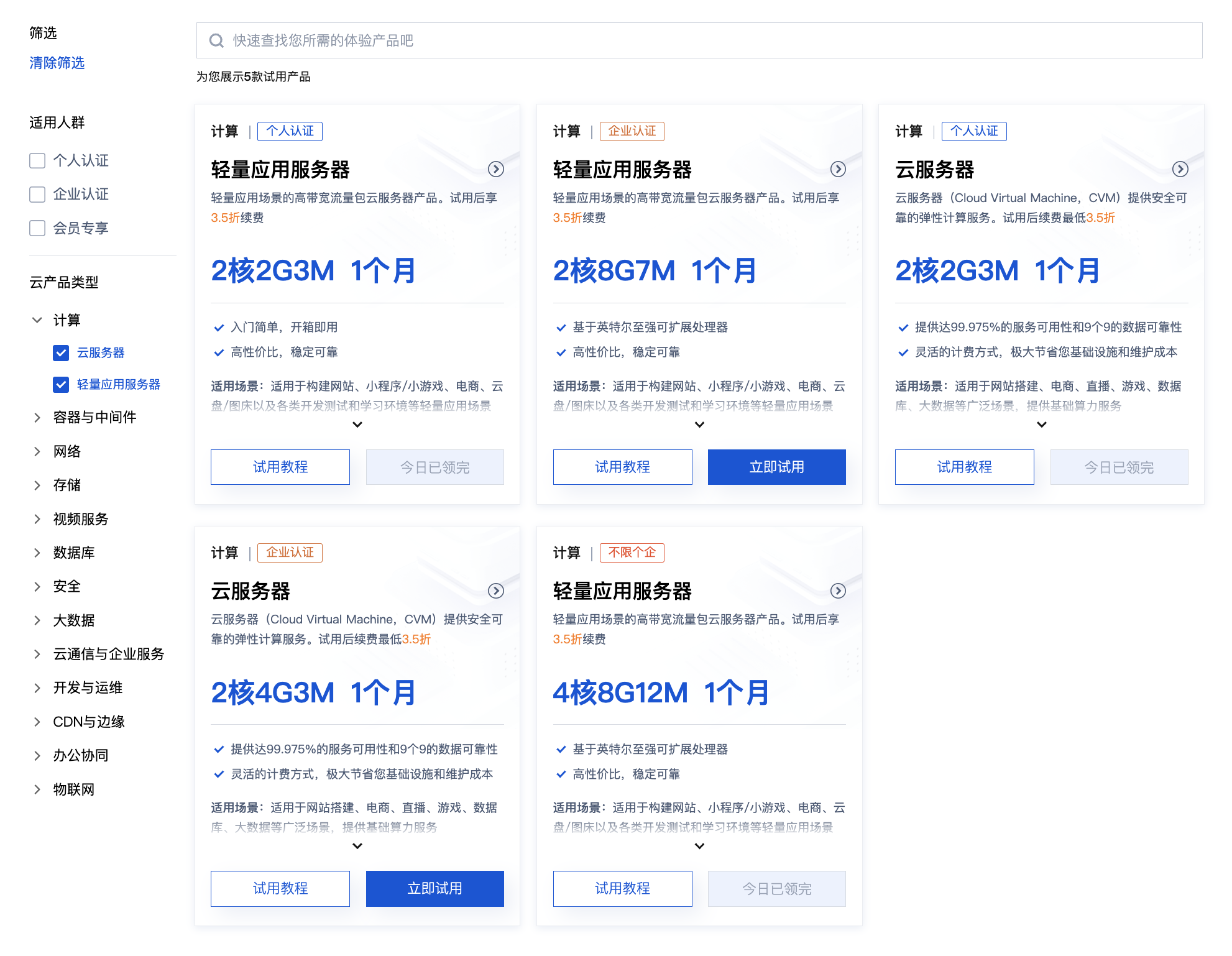
Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
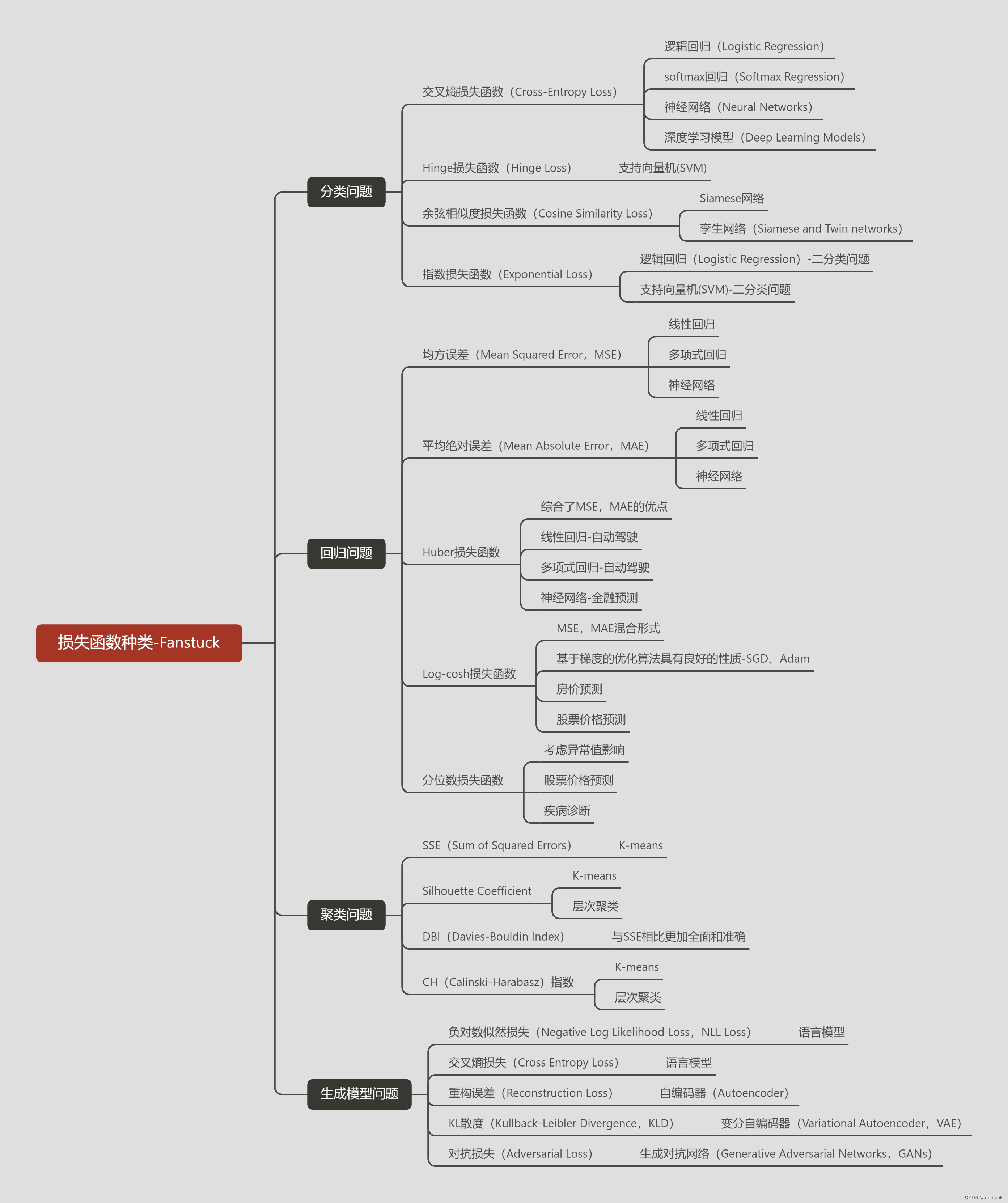
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
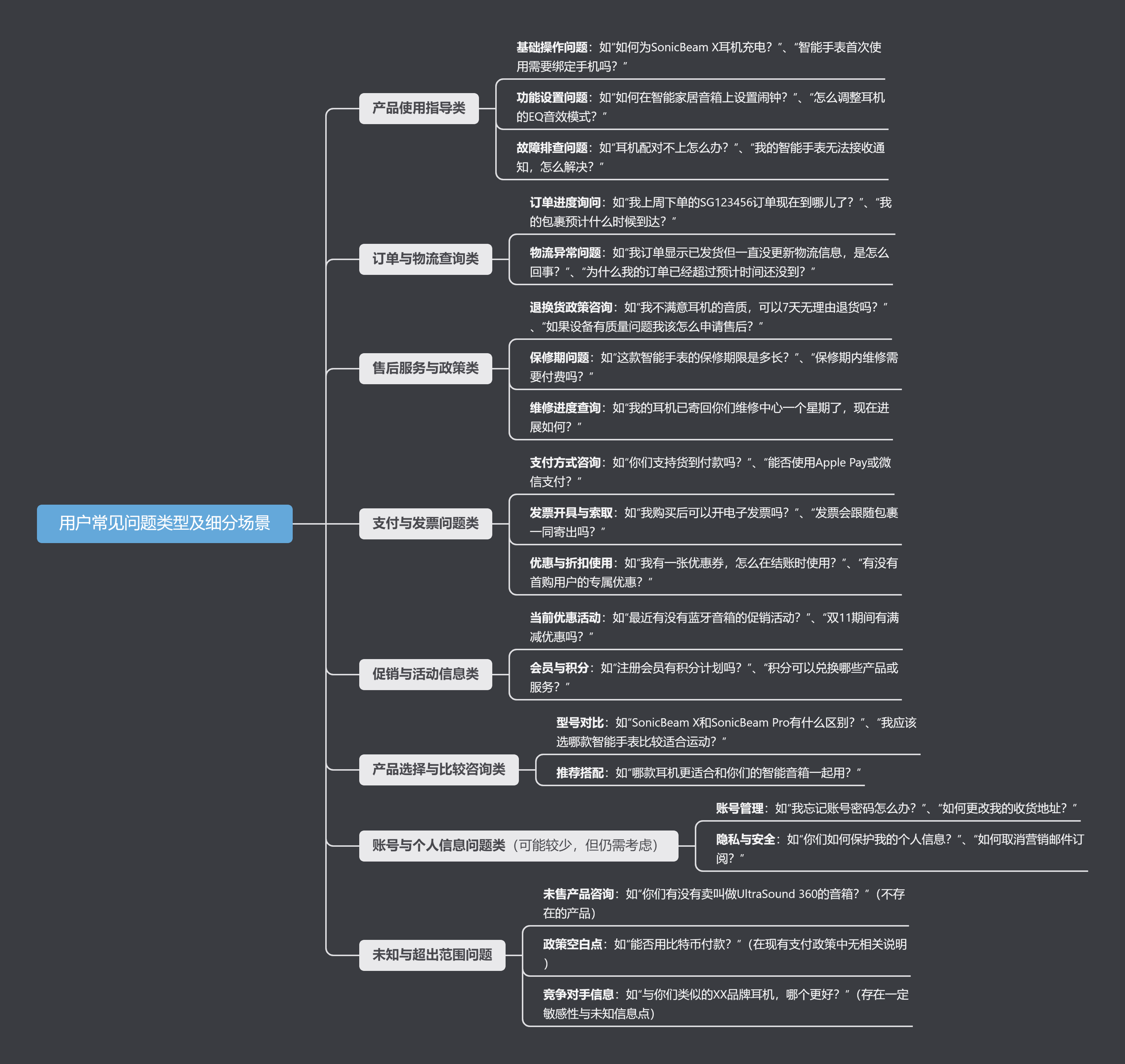
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
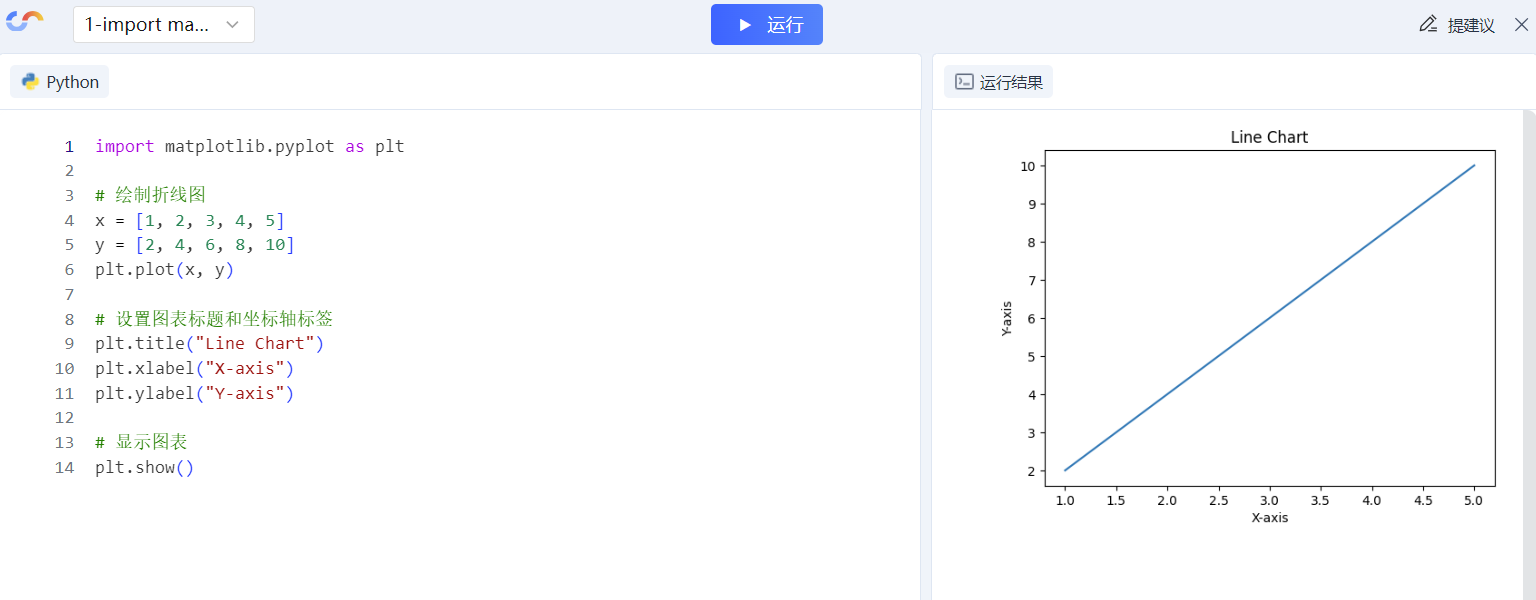
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.