Расширение Шеннона или разложение Шеннона — это метод преобразования булевых функций. Он может выразить любую логическую функцию как любую переменную, умноженную на подфункцию, плюс обратную переменную этой переменной, умноженную на другую подфункцию, как показано в следующих двух формулах.

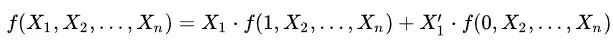
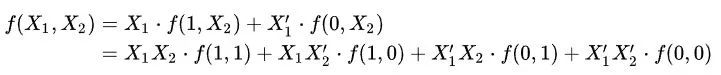
Используя теорему Шеннона о расширении логистической функции, вы можете использовать извлеченную переменную в качестве сигнала выбора, а затем использовать селектор данных для реализации функции. Например:

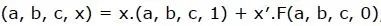
В результате получается следующая схема:

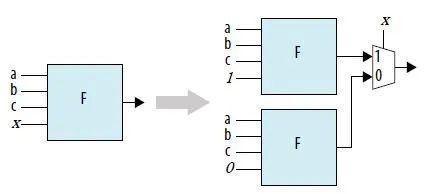
В этой схеме возникает ситуация, когда один из входных портов всегда равен 1 или 0. Инструмент дополнительно оптимизирует это во время логического синтеза, как показано на рисунке ниже.

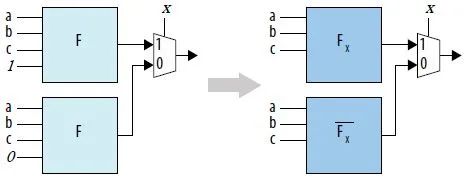
Фактически, теорему о разложении Шеннона можно многократно использовать для приведенной выше схемы, чтобы сформировать схему, показанную на рисунке ниже.

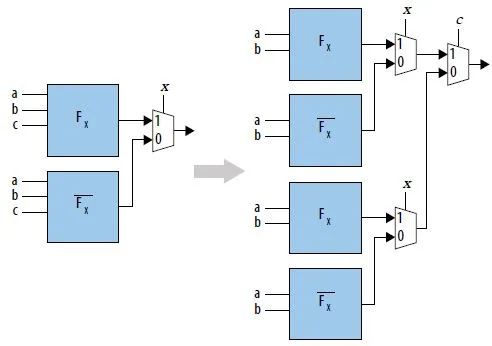
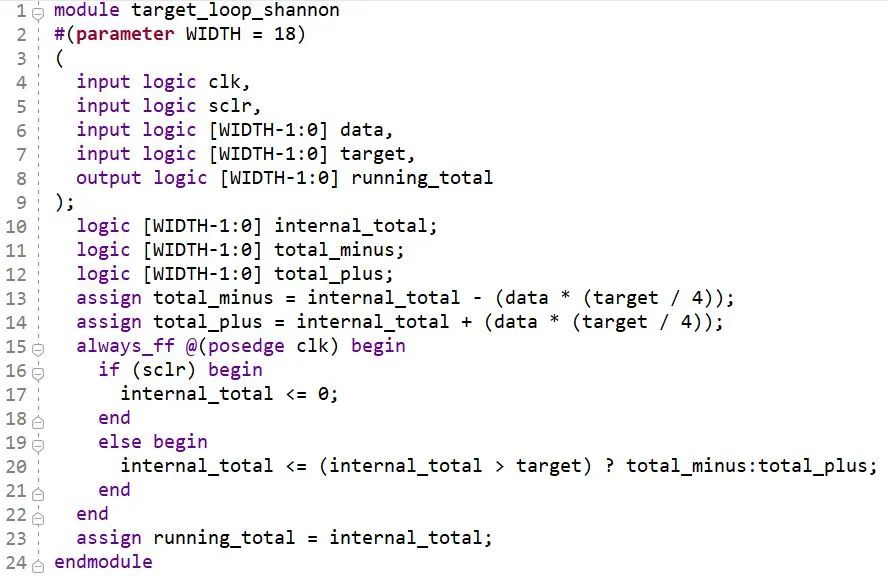
Теорема расширения Шеннона особенно существенно улучшает логические циклы. Как показано на рисунке ниже, из-за существования циклов путь, отмеченный на рисунке красным, не работает правильно после его вставки в регистр конвейера.

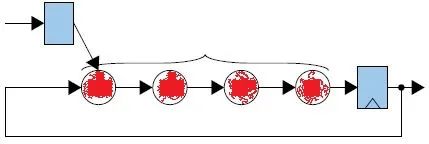
Конвейерные регистры можно добавлять только вне цикла, что требует использования теоремы расширения Шеннона. Извлеките коэффициенты обратной связи и установите их равными 0 и 1 соответственно, тем самым открывая цикл для формирования двух независимых путей и добавляя селектор данных с двумя вариантами в конце пути, конец управления которого обеспечивается выходной обратной связью, и, наконец, образует следующий рисунок: показана схема.

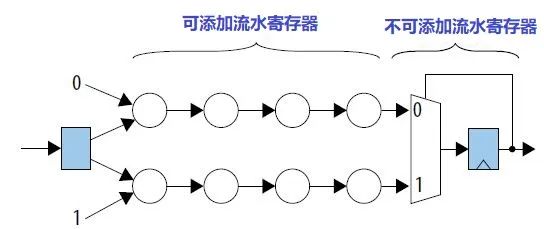
Давайте рассмотрим случай: фрагмент кода, показанный на рисунке ниже. Обратите внимание, что строка 17 образует цикл обратной связи, и именно цикл обратной связи становится узким местом в производительности синхронизации. Этот путь имеет как таблицы поиска, так и DSP (реализующий операции умножения) и не содержит дополнительных регистров конвейера.

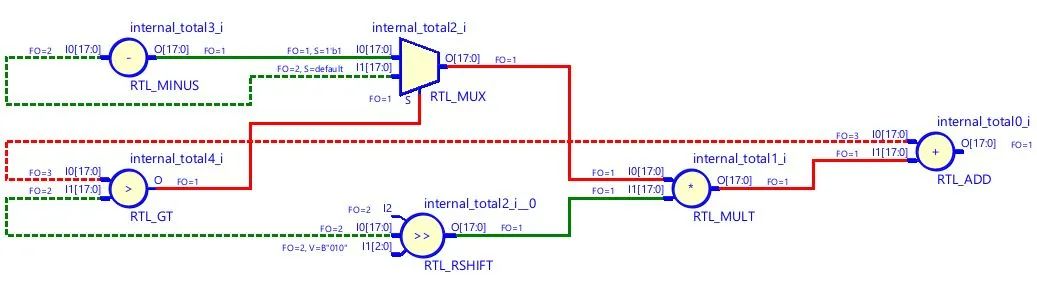
Основываясь на теореме расширения Шеннона, мы оптимизировали код до следующей формы. Обратите внимание, что в строках 13 и 14 кода добавлены две новые переменные, соответствующие ситуации, когда Internal_total больше целевого и меньше целевого значения соответственно, тем самым открывая. петля.

При сравнении двух вышеуказанных схем целевой чип — xcvp1502, тактовая частота — 400 МГц, используется Vivado2023.2. Окончательная производительность показана на рисунке ниже. Видно, что после использования теоремы о разложении Шеннона WNS увеличивается с исходного -0,719 до -0,210. Но все еще не достиг цели в 400 МГц. На этом этапе мы можем продолжить оптимизацию.

Поскольку в этот момент цикл уже открыт, мы можем вставить соответствующие регистры конвейера, как показано на рисунке ниже. Красный прямоугольник на рисунке представляет регистр конвейера. Это может еще больше улучшить WNS, и итоговое значение WNS равно 0,841, что означает, что эта часть пути может работать как минимум до 500 МГц.

Авторские права @ Технологическая станция FPGA

По вопросам перепечатки пишите в личное сообщение | Перепечатка разрешена только после получения разрешения.