Нарастающий фронт сигнала и полоса пропускания системы
Электромагнитные помехи повсюду,Каждый дизайнер должен с этим столкнуться. Чтобы эффективно подавлять,Обычно отправной точкой является решение проблемы целостности сигнала. Этот контент взят из «Анализ целостности сигнала и целостности питания».,Переход от мелкого к глубокому из временной области в частотную область,И с этой точки зрения объясняется внутренняя связь Нарастающего фронтального сигнала и системы пропускания. Фиолетовый текст — это гиперссылка.,Нажмите, чтобы автоматически перейти к соответствующему сообщению в блоге.
Оглавление:
1. Временной интервал
2. Синусоидальный сигнал в частотной области.
3. Характеристики синусоиды
4. Преобразование Фурье★
5. Спектр повторяющихся сигналов
6. Спектр идеального прямоугольного сигнала.
7. Обратное преобразование из частотной области во временную область.
8. Влияние пропускной способности на нарастающий фронт
9. Нарастающий фронт и пропускная способность★
10. Значение слова «эффективный»
11. Пропускная способность★
1. Полоса пропускания фактического сигнала
2. Тактовая частота и полоса пропускания
3. Измеренная полоса пропускания
4. Полоса пропускания модели
5. Пропускная способность межсоединения
1. Временной интервал
Временная область — это реальный мир, единственная реальность, которая существует на самом деле. Временная область — это реальный мир, в котором мы живем, в котором работают высокоскоростные цифровые продукты. При оценке производительности цифровых продуктов анализ обычно выполняется во временной области. Потому что производительность продукта в конечном итоге измеряется во временной области.
Например,Двумя важными параметрами тактового сигнала являются период тактового сигнала и нарастающий фронт.Рисунок 1.1 иллюстрирует эти характеристики. На рисунке показаны период тактовой частоты и нарастающий фронт тактового сигнала 1 ГГц от 10% до 90%. Задний фронт обычно короче нарастающего и иногда вызывает больше шума.
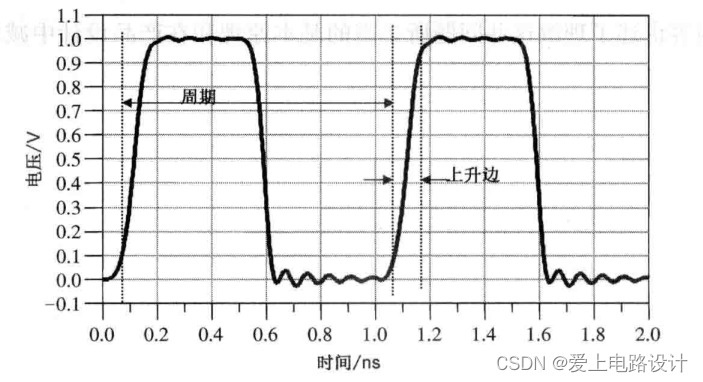
Рисунок 1.1 Типичная форма тактового сигнала
2. Синусоидальный сигнал в частотной области.
Самым важным свойством частотной области является то, что она не реальна, а является математической конструкцией. Синусоидальные волны — единственные формы сигналов, существующие в частотной области. Это самое важное правило в частотной области, то есть синусоидальные волны — это язык частотной области.
Инженеры часто предпочитают использовать синусоидальные волны в частотной области, поскольку любую форму сигнала во временной области можно синтезировать с помощью синусоидальной волны. Это очень важное свойство синусоидальных волн. Однако это не уникальное свойство синусоидальных волн; есть много других сигналов, которые разделяют это свойство.
Фактически, синусоидальные волны обладают следующими четырьмя свойствами, что делает их очень эффективными при описании любой другой формы сигнала:
① Любая форма сигнала во временной области может быть полностью и однозначно описана комбинацией синусоидальных волн.
②Любые две синусоидальные волны с разными частотами ортогональны. Если вы перемножите две синусоидальные волны и проинтегрируете их по всей оси времени, интегрированное значение будет равно нулю. Это показывает, что разные частотные составляющие можно отделить друг от друга.
③Синусоида имеет идеальное математическое определение.
④ Синусоидальные волны и их дифференциальные значения существуют повсюду, без верхних или нижних границ. Реальный мир бесконечен, поэтому синусоидальные волны можно использовать для описания форм сигналов в реальности.
Для различных типов электрических проблем, часто возникающих при целостности сигнала, иногда можно получить удовлетворительные ответы быстрее, используя синусоидальные волны.
Если вы посмотрите на схемы межсоединений, вы обнаружите, что они часто включают в себя комбинацию резисторов, катушек индуктивности и конденсаторов. Эти компоненты в схеме могут быть описаны линейными дифференциальными уравнениями второго порядка, а решением дифференциального уравнения этого типа является синусоидальная волна. В схемах этого типа фактически генерируемый сигнал представляет собой комбинацию сигналов, соответствующих решению приведенного выше дифференциального уравнения.
На практике сначала постройте схему, содержащую R, L и C, и введите сигнал произвольной формы. Во многих случаях будет получена форма волны, похожая на синусоидальную. Более того, эти сигналы можно легко описать комбинациями нескольких синусоид, как показано на рисунке 2.1.
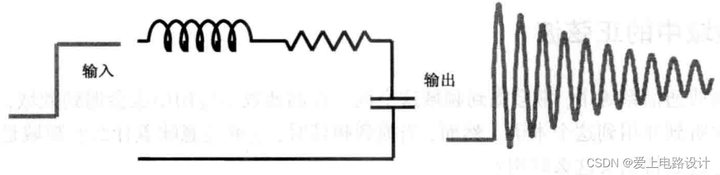
Рисунок 2.1. Поведение быстрых фронтов во временной области, взаимодействующих с идеальной RLC-схемой.
в частотной области Некоторые проблемы легче понять и описать, чем во временной области.。Например,Полоса пропускания — это концепция частотной области, которая описывает наиболее значимую составляющую частоты синусоидальной волны, связанную с сигналом, измерением, моделью или межсоединением.
3. Характеристики синусоиды
Описание синусоидальных волн во временной области,Используйте следующее3термин может адекватно описать синусоидальную волну:частота, амплитуда и фаза,В частотной области он представлен только в виде точки.
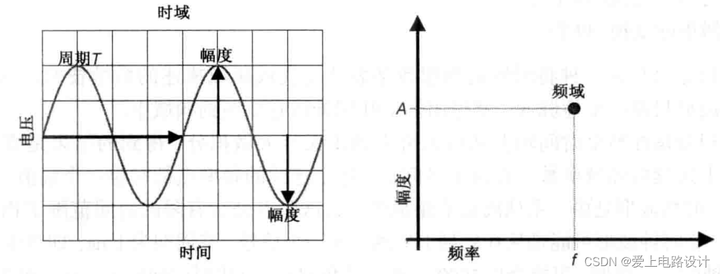
Рисунок 3.1 Синусоидальный сигнал во временной и частотной областях
Слева: описание синусоидальной волны во временной области, состоящей из более чем 1000 точек данных напряжения-времени. Справа: описание синусоидального сигнала в частотной области. Видно, что во временной области единственное, что нужно обсуждать, — это синусоидальная волна, и все, что нужно определить, — это частота, амплитуда и фаза. Если вы описываете только синусоидальную волну, вам понадобятся только эти три величины, чтобы полностью описать ее.
частота:использоватьfвыражать,единицаHz;Связь между частотой синусоидальной волны и ее угловой частотой:ω = 2πф. Греческая буква ω часто используется для обозначения угловой частоты, измеряемой в рад/с.
Амплитуда:Наибольшее значение высоты гребня выше среднего значения。Пиковое значение волны ниже горизонтальной оси и выше горизонтальной оси равны。Для идеальной синусоидальной волны、Значение постоянного тока или среднее значение всегда равно нулю.
Фаза:дает начальное положение волны в начале оси времени。фаза по кругу、радиан(rad)или степень(°)为единица,В круге 360°.
Если фаза временно игнорируется,Постройте синусоидальную волну в частотной области,Требуется только одна точка данных,Это основная причина изучения проблемы в частотной области. Форма сигнала может быть представлена во временной области с использованием тысяч точек данных напряжения-времени.,в частотной областизатем превратился вамплитудно-частотныйточки данных。
Для нескольких частотных точек,Совокупность его амплитуд называется спектром. Спектр каждого сигнала во временной области имеет свою уникальную структуру.,Единственный способ рассчитать спектр сигнала во временной области — это преобразование Фурье.
4. Преобразование Фурье★
Отправной точкой использования частотной области является возможность преобразования формы сигнала из временной области в частотную область, что можно сделать с помощью преобразования Фурье. Существует три типа изменений Фурье:
①Интеграл Фурье (ФИ)
②Дискретное преобразование Фурье (ДПФ)
③Быстрое преобразование Фурье (БПФ)
Интеграл ФурьеЭто математический метод, который преобразует идеальные математические выражения во временной области в описания в частотной области.。Например,Если вся форма сигнала во временной области представляет собой всего лишь короткий импульс,就可использовать Интеграл Фурье преобразует его в частотную область. Интеграл Фурье заключается в интегрировании по всей оси времени от отрицательной бесконечности до положительной бесконечности, и полученный результат представляет собой непрерывную функцию частотной области от нулевой частоты до частоты положительной бесконечности. Внутри этого интервала каждая последующая частотная точка соответствует амплитуде.
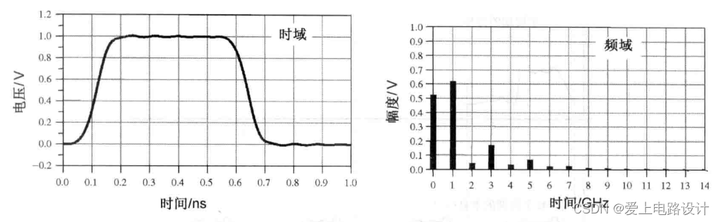
Рисунок 4.1. На левом рисунке показан цикл тактового сигнала частотой 1 ГГц во временной области, а на правом изображении показано его представление в частотной области.
Дискретное преобразование Фурьезаключается в преобразовании формы сигнала в частотную область。Основное предположение состоит в том, что исходная форма сигнала во временной области является периодической.,Это повторяется каждые T секунд. отличается от точек,Здесь используется только суммирование,Любой набор данных можно преобразовать в частотную область с помощью простых математических методов.
Быстрое преобразование Фурье除了计算每个频率点幅度值的实际算法使использовать了快速矩阵代数学的技巧,это связано с Дискретное преобразование Фурье точно такой же. Этот быстрый алгоритм применим только в том случае, если количество точек данных во временной области является целой степенью 2, например 256 точек, 512 точек или 1024 точки. По количеству точек расчетного напряжения Быстрое преобразование Скорость вычислений Фурье может быть в 100–10 000 раз быстрее, чем обычное преобразование Фурье. Быстрое преобразование Фурье может работать только с периодическими сигналами.
Эти три алгоритма различны, но имеют одну и ту же цель — преобразовать форму сигнала во временной области в спектр частотной области.
в частотной области,Описание формы сигнала становится набором синусоид разных частот.。Каждая частотная составляющая имеет соответствующую амплитуду и фазу.。Полный набор всех этих частотных точек и их амплитудных значений называетсяСпектр формы волны.
Многие простые в использовании коммерческие программы могут выполнять вычисления дискретного преобразования Фурье или быстрого преобразования Фурье для входных сигналов произвольной формы. В каждой версии программного обеспечения SPICE есть функция, называемая инструкцией .FOUR, которая может генерировать амплитуду первых 9 частотных компонентов любой формы сигнала. Большинство версий более продвинутых инструментов SPICE также могут использовать ДПФ для расчета полного набора частотных точек и значений амплитуд. В Microsoft Excel есть функция БПФ, которую обычно можно найти в «Надстройке проекта».
5. Спектр повторяющихся сигналов
Дискретное преобразование Фурьеили Быстрое преобразование Фурье используется для преобразования фактической формы сигнала из временной области в частотную область. Вы можете использовать Дискретное для любой измеренной произвольной формы сигнала. преобразование Фурье,Ключевым условием является то, что форма сигнала должна быть повторяющейся, обычно с заглавной буквой F, обозначающей частоту повторения формы сигнала во временной области.
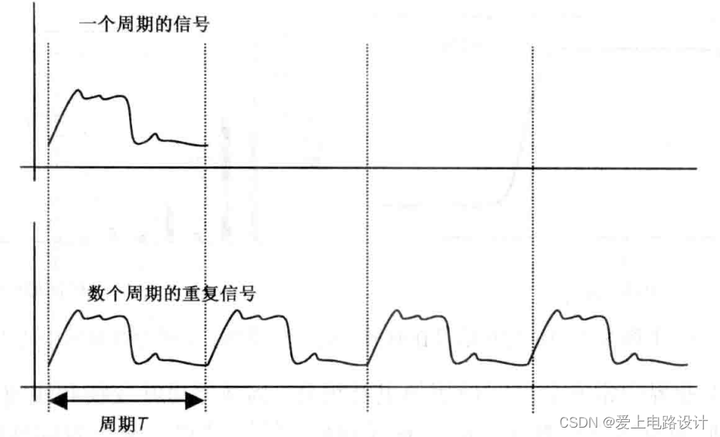
Рисунок 5.1 Любая форма сигнала может стать периодической, а быстрое преобразование Фурье может работать только с периодическими сигналами.
При преобразовании части сигнала в повторяющийся сигнал могут возникнуть разрывы сращивания.Этот неестественный прыжок, происходящий в суставе,Разрывы сплайсинга также будут возникать при Дискретном преобразовании Фурье. Чтобы избежать этой проблемы,Обычно используется оконный фильтр.,Чтобы гарантировать, что напряжение на обоих концах постоянно остается на одном и том же значении. Например,Окно Хэмминга и окно ХэннингаЭто фильтр, реализующий эту функцию。
Частота синусоидальной волны в спектре должна быть целым кратным частоте повторения. Если тактовая частота равна 1 ГГц, дискретное преобразование Фурье имеет только синусоидальные компоненты, такие как 1 ГГц, 2 ГГц и 3 ГГц. Частота первой синусоидальной волны называется 1-й гармоникой, частота второй синусоидальной волны — 2-й гармоникой и так далее. Каждая гармоника имеет разную амплитуду и фазу. Совокупность всех гармоник и их амплитуд называется спектром.
Фактическая амплитуда каждой гармоники определяется по значению, рассчитанному с помощью дискретного преобразования Фурье, и каждая конкретная форма сигнала имеет свой собственный спектр.
6. Спектр идеального прямоугольного сигнала.
Идеальная прямоугольная волна симметрична, имеет рабочий цикл 50% и пиковое значение 1 В.
Если частота повторения идеальной прямоугольной волны равна 1 ГГц, частота синусоидальной волны в спектре является целым кратным 1 ГГц. Мы надеемся увидеть некоторые частотные компоненты, такие как f=1 ГГц, 2 ГГц, 3 ГГц и т. д., но какова амплитуда каждой синусоидальной волны?
Все четные гармоники (например, 2 ГГц, 4 ГГц, 6 ГГц) имеют нулевую амплитуду, только нечетные гармоники имеют ненулевые значения. Это характеристика любого сигнала, в котором вторая половина сигнала является в точности отрицанием первой половины. Мы называем эти формы сигналов антисимметричными или нечетно симметричными сигналами.
Амплитуда An нечетных гармоник равна:

Добавьте комментарий к изображению, не более 140 слов (по желанию)
Где n — порядок гармоники (нечетное число).
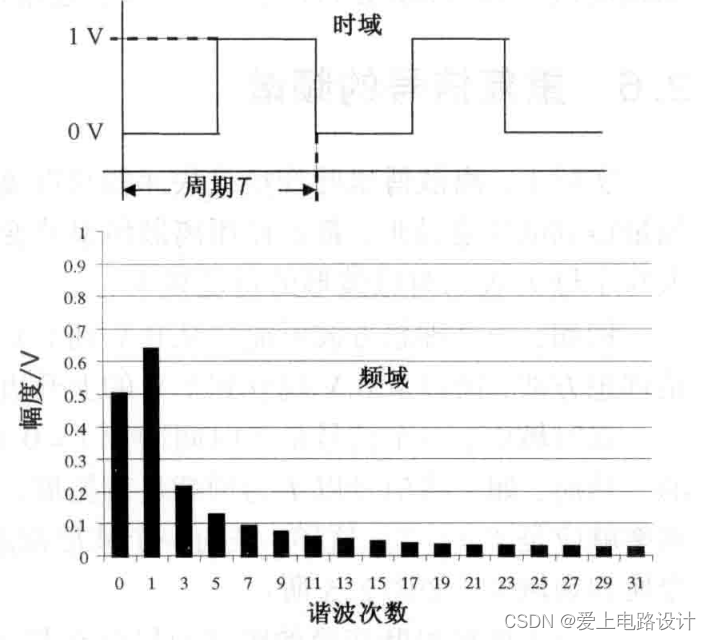
Рисунок 6.1 Идеальная прямоугольная волна во временной и частотной областях
Для идеального прямоугольного сигнала с коэффициентом заполнения 50 % и скачком от 0 В до 1 В амплитуда 1-й гармоники равна 0,63 В, амплитуда 3-й гармоники — 0,21 В, амплитуда 1001-й гармоники — 0,00063 В. Обратите внимание, что с увеличением частоты ее амплитуда уменьшается по мере уменьшения 1/f.
Также есть особая частотная точка: 0Гц. Потому что среднее значение синусоидальной волны равно нулю,Любая комбинация синусоидальных волн может описывать только форму сигнала с нулевым средним значением во временной области. Если разрешено смещение постоянного тока,То есть среднее значение сигнала не равно нулю.,Компонент постоянного тока размещается в точке нулевой частоты. Иногда называется 0-й гармоникой.,Его амплитуда равна среднему значению сигнала (Среднеквадратичное значение/пиковое значение/амплитуда/мгновенное значение)。Рабочий цикл прямоугольной волны 50% В случае , амплитуда 0-й гармоники равна 0,5 В.
Его можно резюмировать следующим образом:
·Совокупность частотных составляющих синусоидальной волны и их амплитуд называется спектром, а каждая составляющая называется гармоникой;
·0-я гармоника – это значение составляющей постоянного тока;
·Для частного случая идеальной прямоугольной волны с рабочим циклом 50% амплитуда четных гармоник равна нулю;
· Амплитуда любой гармоники может быть рассчитана по формуле 2/(nπ).
7. Обратное преобразование из частотной области во временную область.
В частотной области спектр представляет собой амплитуду всех частот синусоидальной волны, содержащихся в форме сигнала во временной области. Если вы знаете спектр и хотите наблюдать его форму сигнала во временной области, вам нужно всего лишь обратно преобразовать каждый частотный компонент в его синусоидальный сигнал во временной области, а затем сложить их все. Этот процесс представляет собой обратное преобразование Фурье.
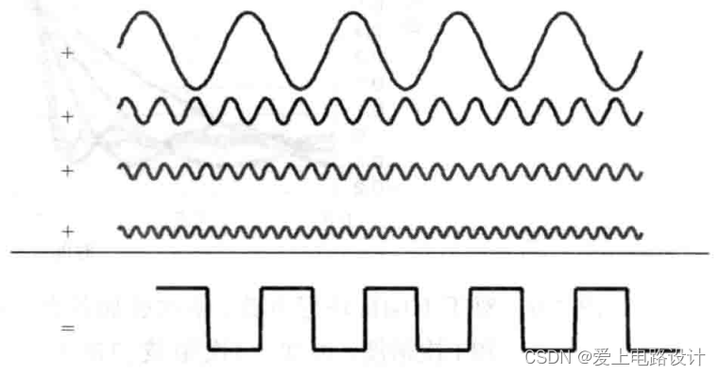
Рисунок 7.1. Путем наложения каждой синусоидальной составляющей, указанной выше, спектр можно преобразовать во временной сигнал.
Для спектра идеальной прямоугольной волны частотой 1 ГГц первый член представляет собой 0-ю гармонику, имеющую амплитуду 0,5 В. Этот компонент описывает постоянную постоянного тока во временной области.
Вторая составляющая — это 1-я гармоника, представляющая собой синусоидальную волну с частотой 1 ГГц и амплитудой 0,63 В во временной области. Он накладывается на предыдущий член для получения синусоидального сигнала со средним сдвигом 0,5 В во временной области. Это не очень хорошее приближение к идеальному прямоугольному сигналу.
Затем добавьте третью гармонику. Амплитуда частотной составляющей синусоидального сигнала 3 ГГц составляет 0,21 В. Если вы наложите ее на существующую форму сигнала во временной области, вы обнаружите, что форма нового сигнала немного изменилась: верхняя часть более гладкая, ближе к прямоугольной, а верхняя часть более гладкая, ближе к прямоугольной. нарастающий фронт короче. По аналогии, добавление всех последовательных высших гармоник к существующей форме сигнала приводит к выводу, который все больше и больше напоминает прямоугольную волну. Стоит отметить, что нарастающий фронт формы сигнала во временной области меняется с добавлением более высоких гармоник.
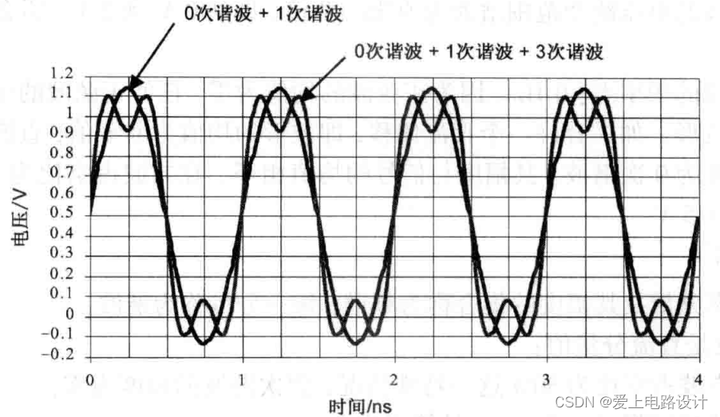
Рисунок 7.1. Для идеального прямоугольного сигнала частотой 1 ГГц форма сигнала во временной области формируется при добавлении 0-й гармоники, 1-й гармоники и затем 3-й гармоники.
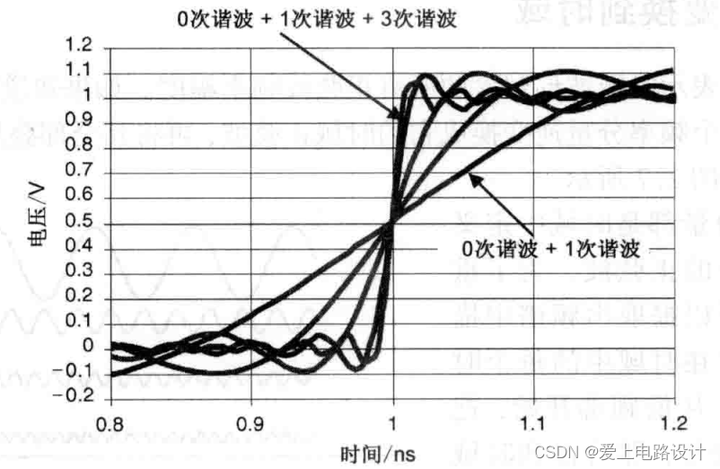
Рисунок 7.2. Для идеального прямоугольного сигнала частотой 1 ГГц форма сигнала во временной области, генерируемая путем последовательного наложения каждой гармоники
Первой является 0-я гармоника и 1-я гармоника, затем 3-я гармоника, 7-я гармоника, 19-я гармоника и, наконец, 31-я гармоника.
8. Влияние пропускной способности на нарастающий фронт
Полоса пропускания представляет собой наибольшее значимое значение частотного компонента синусоидальной волны в спектре.。Выбор полосы пропускания оказывает прямое влияние на самый короткий нарастающий фронт сигнала во временной области.Для цифровых сигналов,Полоса пропускания также относится к диапазону частот в спектре сигнала. Но для цифровых сигналов,Низкочастотный диапазон начинается от составляющей постоянного тока и продолжается до самой высокочастотной составляющей. В области цифровых сигналов,Поскольку самая низкая частота — постоянный ток,Таким образом, полоса пропускания всегда соответствует наибольшему допустимому значению частотной составляющей синусоидальной волны.
Вообще говоря, чем короче нарастающий фронт сигнала во временной области, тем выше полоса пропускания в частотной области.Если изменение спектра уменьшает полосу пропускания сигнала,Тогда нарастающий фронт сигнала станет длиннее.
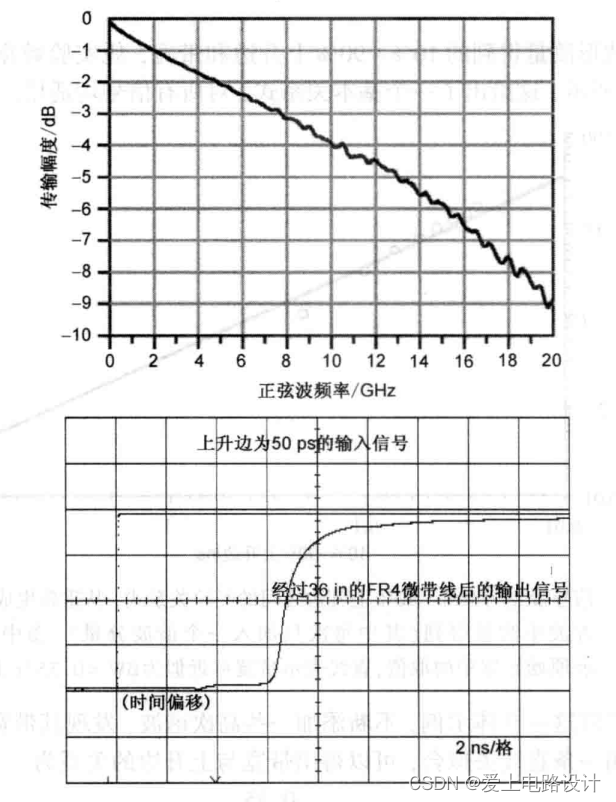
Рисунок 8.1 Затухание линии передачи 50 Ом на плате FR4
Такое избирательное ослабление уменьшает полосу пропускания сигнала, распространяющегося в межсоединении.Рисунок На рисунке ниже в 8.1 показан сигнал с нарастающим фронтом 50 пс, входящий в FR4. Форма сигнала при наличии на плате линии передачи длиной 36 дюймов и при выходе из линии передачи. Поскольку высокочастотная составляющая ослабляется сильнее, ее нарастающий фронт ухудшается с 50 пс до 1,5 нс.
Поскольку высокочастотная составляющая ослабляется сильнее, ее нарастающий фронт увеличивается с 50 пс до почти 1,5 нс. Обычно используются линии длиной 36 дюймов. Например, при использовании двух сменных плат длиной 6 дюймов и объединительной платы длиной 24 дюйма длина проводов составляет 36 дюймов. Основным ограничением, препятствующим использованию стеков FR4 в высокоскоростных каналах связи, превышающих 1 ГГц, является ухудшение нарастающего фронта.
Вообще говоря, чем короче нарастающий фронт сигнала во временной области, тем выше полоса пропускания в частотной области. Если вы измените спектр так, чтобы полоса пропускания сигнала уменьшилась, нарастающий фронт сигнала станет длиннее.
9. Нарастающий фронт и пропускная способность★
Во время регенерации идеального прямоугольного сигнала можно количественно оценить соотношение между используемой полосой пропускания и его нарастающим фронтом. В предыдущем примере регенерации идеального прямоугольного сигнала полоса пропускания, соответствующая каждому синтезированному сигналу, была очевидна. Потому что каждая форма волны искусственно синтезируется путем добавления частотной составляющей синусоидальной волны определенной гармоники. Определенный нарастающий фронт 10–90 % также можно измерить по графику во временной области.
Если известны нарастающий фронт 10–90 % и полоса пропускания, измеренная для каждой формы сигнала, на основе экспериментальных данных можно построить простую зависимость. Как показано на рисунке 9.1, это дает базовую зависимость, применимую ко всем сигналам.
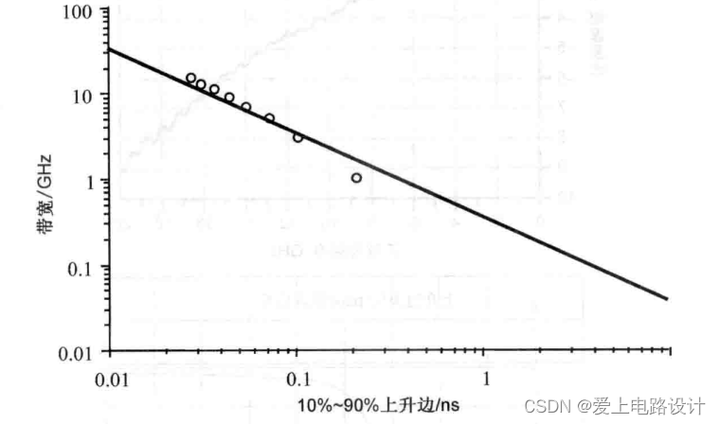
Рисунок 9.1 Экспериментальные данные
В конкретном примере регенерации прямоугольной волны я продолжал добавлять несколько высших гармоник и обнаружил, что полоса пропускания связана с обратной стороной нарастающего фронта. Мы сопоставляем эти точки прямой линией и можем получить зависимость между полосой пропускания и нарастающим фронтом следующим образом:
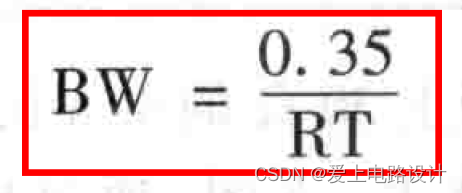
Добавьте комментарий к изображению, не более 140 слов (по желанию)
Среди них BW представляет полосу пропускания (единицы ГГц), RT представляет собой нарастающий фронт 10% ~ 90% (единицы н С).
Например, если нарастающий фронт сигнала составляет 1 нс, его полоса пропускания составит примерно 0,35 ГГц или 350 МГц. Аналогично, если полоса пропускания сигнала составляет 3 ГГц, нарастающий фронт составит около 0,1 нс. В системе на базе DDR3 нарастающий фронт сигнала может составлять 0,25 нс, поэтому его полоса пропускания составляет 0,35/0,25 нс = 1,4 ГГц.
Для других форм сигналов,Формы сигналов, такие как гауссовы или экспоненциальные фронты,Вы также можете использовать другие методы для получения таких отношений. Для прямоугольной волны,Принятый подход был чисто экспериментальным.,Никаких предположений не было сделано。Эта экспериментальная формула представляет собой очень полезное эмпирическое правило.
Очень важно обеспечить согласованность единиц измерения. Если единицей измерения нарастающего фронта является мкс, то единицей измерения полосы пропускания должно быть МГц. Например, для длинной полосы пропускания восходящей стороны 10 мкс она равна 0,35/10 мкс = 0,035 МГц, что составляет 35 к Гц.
Например, если единицей нарастающего фронта является н С, единицей ширины полосы является ГГц. Для типичного тактового сигнала частотой 10 МГц нарастающий фронт обычно составляет 10 нс, а его полоса пропускания составляет примерно 0,35/10 нс = 0,035 ГГц, что составляет 35 МГц.
10. Значение слова «эффективный»
Полоса пропускания сигнала определяется как наивысшая допустимая составляющая частоты синусоидальной волны. Если включены все частотные компоненты в пределах полосы пропускания, можно восстановить прямоугольную волну с ограниченным нарастающим фронтом. В это время соотношение между нарастающим фронтом и полосой пропускания составляет: нарастающий фронт RT = 0,35/BW.
Для реальных сигналов во временной области,По мере увеличения частоты,Амплитуда его спектральных составляющих всегда убывает быстрее, чем амплитуда той же частоты в идеальном прямоугольном сигнале. Вопрос эффективности на самом деле является вопросом частоты.,Амплитуды гармонических составляющих выше этой точки меньше амплитуд соответствующих частотных составляющих идеальной прямоугольной волны. Так называемый «маленький»,Обычно это означает, что мощность этой составляющей меньше соответствующей мощности идеальной прямоугольной волны.50% мощности частотной составляющей, мощность падает на 50%, то есть амплитуда падает до 70%. Это истинное определение эффективности.Если амплитуда выше, чем амплитуда той же гармоники в идеальной прямоугольной волне70%Вот и все,называется действительным.
Взгляд под немного другим углом,может быть эффективнымОпределяется как точка частоты, в которой гармонические компоненты фактического сигнала начинают уменьшаться быстрее, чем 1/f,Эту частоту еще называютЧастота вращения.
Сравнивая спектр прямоугольной волны и фактический спектр трапецеидальной волны, мы видим, что 1-я и 3-я гармоники этих двух примерно одинаковы. 5-я гармоника трапецеидальной волны составляет около 70% прямоугольной волны. по-прежнему составляет большую часть. Однако 7-я гармоника трапециевидной волны составляет лишь 30% идеальной прямоугольной волны.
Изучая спектр трапециевидных волн, можно сделать следующие выводы:
Амплитуда гармонической составляющей выше 5-го порядка (например, 7-й гармоники или выше) эквивалентна лишь очень небольшой части общего напряжения идеальной прямоугольной волны. Поэтому их влияние на нарастающий фронт также минимально. По сравнению с идеальной прямоугольной волной из спектра видно, что самой высокой эффективной составляющей синусоидальной волны в трапециевидной волне является 5-я гармоника, которая аппроксимируется.
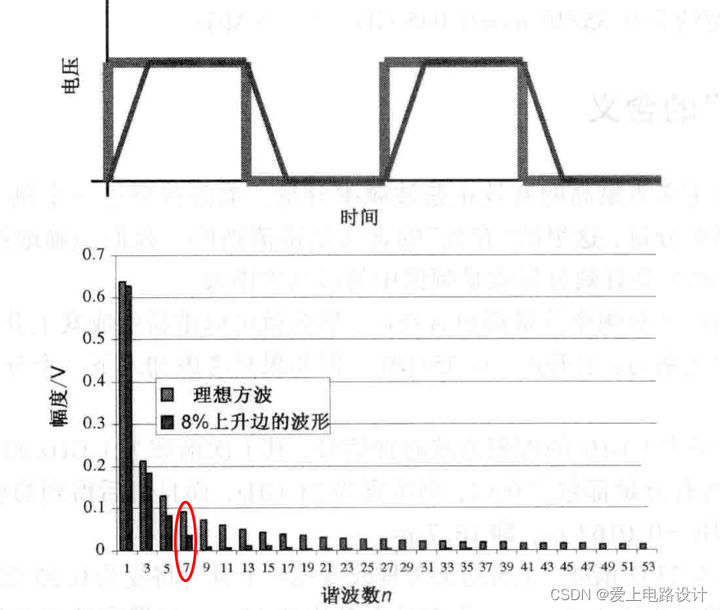
Добавьте комментарий к изображению, не более 140 слов (по желанию)
Вверху: сигнал во временной области с частотой 1 ГГц, идеальная прямоугольная волна и идеальная трапециевидная волна с нарастающим фронтом 0,08 нс; Ниже: это видно из диаграммы спектра двух,Высшие гармоники идеальной трапециевидной волны резко падают по сравнению с идеальной прямоугольной волной.。Это также отражает то, что нарастающий фронт обратно пропорционален полосе пропускания. Чем длиннее нарастающий фронт, тем уже полоса пропускания; чем длиннее нарастающий фронт, тем меньше в нем высокочастотных компонентов и тем быстрее спадают гармоники высокого порядка.
11. Пропускная способность★
1. Полоса пропускания фактического сигнала
Простая характеристика высококачественных сигналов, близких к идеальным прямоугольным волнам, заключается в том, что если линия передачи плохо завершена, сигнал будет звонким, а пик спектра будет соответствовать частоте звонка. Амплитуда на частоте звонка будет более чем в 10 раз превышать амплитуду сигнала без звонка. Электромагнитные помехи вызваны излучением каждой частотной составляющей электрического тока. Наиболее серьезным источником излучения является синфазный ток, общее излучение которого будет линейно увеличиваться с частотой.
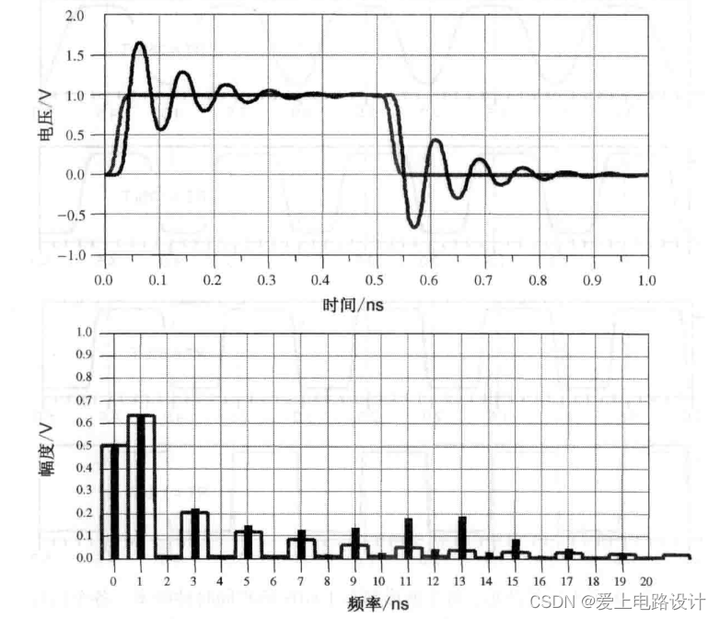
Рисунок 11.1.1
Пропускная способность со звонком значительно выше, чем без звонка. Когда в сигнале возникает звон, его полоса пропускания примерно равна частоте звона. Однако использование только этой полосы пропускания для характеристики вызывного сигнала может ввести в заблуждение. Лучшим подходом является рассмотрение всего спектра.
Электромагнитные помехи вызваны излучением каждой частотной составляющей электрического тока. Наиболее серьезным источником излучения является синфазный ток, общее излучение которого будет линейно увеличиваться с частотой. Это показывает, что если ток имеет характеристики идеальной прямоугольной волны, хотя амплитуда каждой гармоники уменьшается со скоростью 1/f, способность излучения все равно будет увеличиваться со скоростью f. Следовательно, влияние каждой гармоники на электромагнитные помехи одинаково. Чтобы уменьшить электромагнитные помехи, конструкции должны использовать минимально возможную полосу пропускания для всех сигналов. Выше этой полосы амплитуда гармоники уменьшается быстрее, чем 1/f, и влияние на излучение будет меньшим. Сведите ширину полосы пропускания к минимуму, и количество излучения будет сведено к минимуму.
Звон в цепи может увеличить амплитуду высокочастотных составляющих и увеличить интенсивность их излучения в 10 раз. Это одна из причин, почему для уменьшения электромагнитных помех мы обычно начинаем с решения проблем целостности сигнала.
2. Тактовая частота и полоса пропускания
Пропускная способность напрямую связана с нарастающим фронтом сигнала. Для двух разных сигналов, даже с одинаковой тактовой частотой, нарастающий фронт и полоса пропускания, скорее всего, будут разными.
Та же тактовая частота 1 ГГц. Каждый сигнал имеет свой нарастающий фронт,Различные пропорции в цикле,Так что пропускная способность у них тоже разная。Важно отметить, что полосу пропускания определяет не тактовая частота, а нарастающий фронт.Если вы знаете только тактовую частоту сигнала,Невозможно определить его пропускную способность.
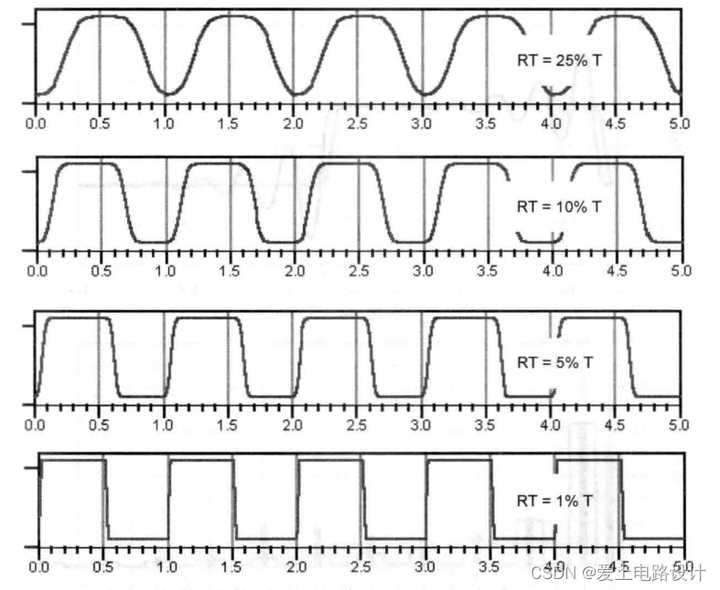
Рисунок 11.2.1
В фактической форме тактового сигнала,Какова связь между нарастающим фронтом и тактовым циклом??Единственное ограничение между ними заключается в том, что нарастающий фронт должен составлять менее 50% периода.
Если вы не знаете отношение нарастающего фронта к периоду,Разумное эмпирическое правило таково: нарастающий фронт составляет 7% тактового цикла.Это работает со многими микропроцессорными платами иASICСитуация с автобусом уровня вождения близка к。
Имейте в виду, что предположение о том, что нарастающий фронт составляет 7% периода, является сложным. Во многих системах этот показатель приближается к 10 %, поэтому наши предположения относительно нарастающего фронта короче, чем в типичных ситуациях. Таким образом, нарастающий фронт недооценивается, а пропускная способность недооценивается, что гораздо безопаснее, чем недооценка пропускной способности. Пропускная способность составляет примерно 0,35/нарастающий фронт, что составляет 7% периода. А поскольку период и частота являются обратными друг другу величинами, можно определить соотношение между ними, то есть полоса пропускания в 5 раз превышает тактовую частоту:
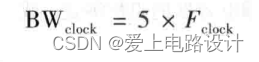
Добавьте комментарий к изображению, не более 140 слов (по желанию)
Среди них BWтакт представляет собой приблизительное значение полосы пропускания тактовой частоты (в ГГц), а F представляет тактовую частоту (в ГГц). Например, если тактовая частота равна 100 МГц, полоса пропускания сигнала равна 500 МГц. Если тактовая частота равна 1 ГГц, полоса пропускания сигнала составляет 5 ГГц. Основываясь на предположении, что нарастающий фронт составляет 7% от тактового периода, делается приведенный выше приблизительный вывод. Учитывая это предположение, есть два полезных практических правила, с помощью которых можно легко оценить пропускную способность. Другими словами, типичной самой высокой частотной составляющей синусоидального сигнала в форме тактового сигнала является 5-я гармоника. Очевидно, что по-прежнему желательно всегда иметь возможность оценить пропускную способность непосредственно по нарастающему фронту. Однако, к сожалению, не всегда возможно узнать нарастающий фронт сигнала, и ответ может потребоваться немедленно!
3. Измеренная полоса пропускания
от Измерьте сопротивление развязывающих конденсаторов от 1 МГц до 1 ГГц.,Видно, что при частоте ниже 10 МГц,Импеданс ведет себя как идеальный конденсатор.,Но выше 10 МГц,Он ведет себя как идеальный индуктор. Во всем диапазоне измерений векторного анализатора цепей (в данном примере до 1 ГГц),Измеренная полоса пропускания1GHz。Измеренная полоса пропускания отличается от доступной полосы пропускания самого компонента.
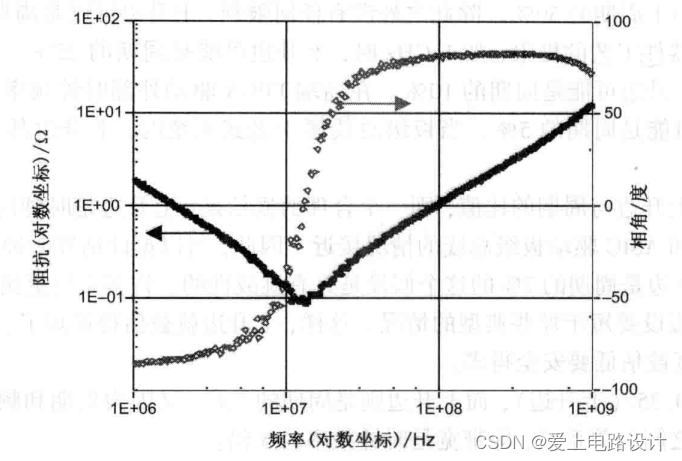
Рисунок 11.3.1 Измерение импеданса керамического развязывающего конденсатора C1206, полоса измерения данных составляет 1 ГГц.
4. Полоса пропускания модели
Полоса пропускания модели относится к самой высокой синусоидальной частотной составляющей, для которой модель может быть точно использована для прогнозирования истинных характеристик фактической конструкции.
Простая модель исходной цепи состоит из последовательно соединенных идеального индуктора и идеального резистора. До частоты 2 ГГц импеданс, оцененный с использованием соответствующих параметров L и R, очень согласуется с фактически измеренным импедансом, поэтому полоса пропускания этой простой модели составляет 2 ГГц.
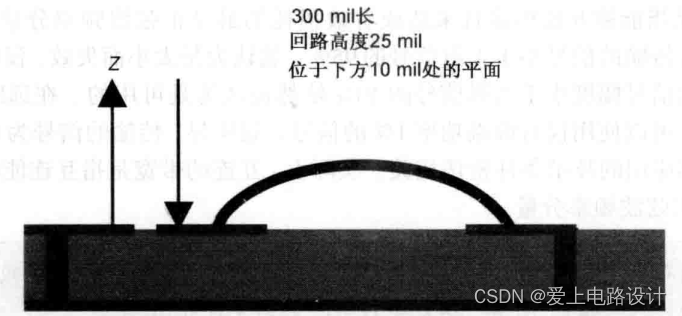
Рисунок 11.4.1 Схематическая диаграмма петли соединительного провода между двумя контактными площадками, где обратный путь находится примерно на 10 мил ниже соединительного провода.
За пределами 2 ГГц использование модели с более широкой полосой пропускания позволяет оценить импеданс фактического соединительного провода на более высоких частотах. В настоящее время необходимо учитывать влияние емкости контактной площадки и разработать новую модель, то есть модель второго порядка.
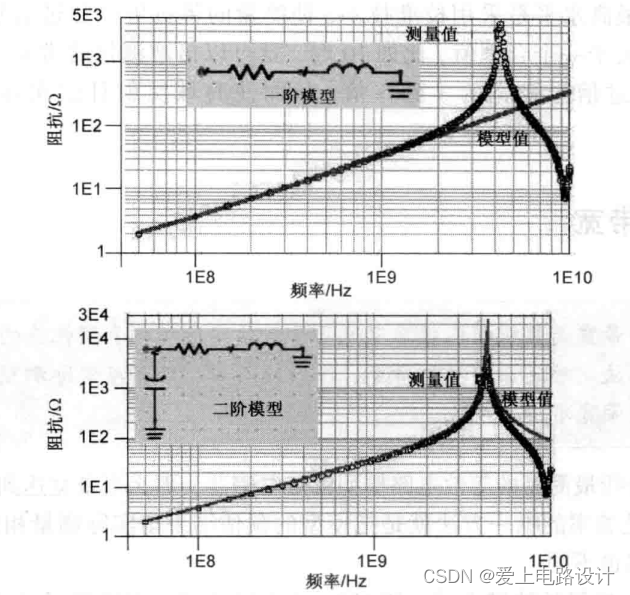
Рисунок 11.4.2
Вверху: Измеренный импеданс по сравнению с результатами моделирования модели первого порядка. Эти два параметра очень стабильны, пока полоса пропускания не достигнет 2 ГГц. Внизу: Измеренный импеданс по сравнению с результатами моделирования модели второго порядка. Эти два параметра очень стабильны, пока полоса пропускания не достигнет 4 ГГц. Эта картина была получена зондовой станцией GigaTest Labs с полосой измерения 10 ГГц.
5. Пропускная способность межсоединения
Пропускная способность межсоединения — это наивысшая составляющая синусоидальной частоты, которая может передаваться межсоединением, не вызывая эффективных потерь. Что такое «эффективный»? В некоторых приложениях, если передаваемый сигнал составляет менее 95% падающего сигнала, он считается слишком маленьким, недействительным и не может быть использован. В других случаях амплитуда передаваемого сигнала составляет менее 10% от падающего сигнала и все равно считается пригодной к использованию.
В кабельных системах дальнего телевидения,Приемник может даже использовать сигнал с мощностью всего 1% от мощности источника. Это очевидно,Концепция того, насколько большой передаваемый сигнал считается эффективным.,Тесно связано с техническими условиями конкретного применения. на самом деле,Пропускная способность межсоединения — это наивысшая составляющая синусоидальной частоты, которую может передавать межсоединение и которая соответствует техническим условиям приложения.
Вообще говоря,«Эффективный» на практике означает снижение амплитуды передаваемой частотной составляющей на 3 д Б.,То есть амплитуда снижается до падающего значения70%。Это то, что часто упоминаетсяПропускная способность межсоединения 3 д Б.
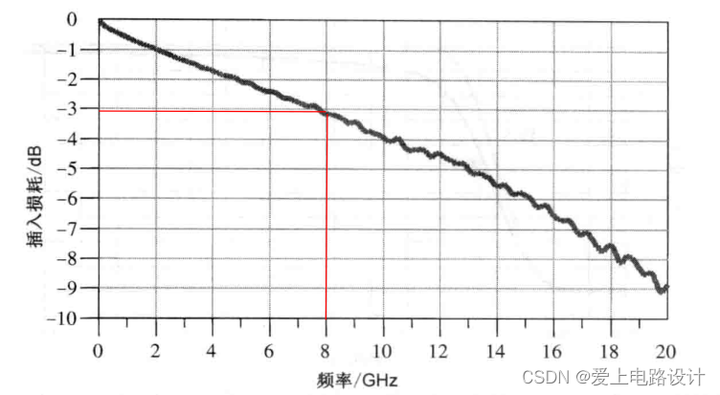
Рисунок 11.5.1 Амплитудные значения синусоидальных сигналов разных частот, измеренные через линию передачи 4в на плате FR4
Для данного сечения и свойств материала в этом примере полоса пропускания 3 д Б составляет примерно 8 ГГц. Эту картину зафиксировала зондовая станция GigaTest Labs. Пропускную способность межсоединения можно приблизительно объяснить следующим сценарием: если через межсоединение передается идеальная прямоугольная волна, может передаваться каждая составляющая синусоидального сигнала ниже 8 ГГц, а амплитуда до и после передачи примерно одинакова, но компоненты выше 8 ГГц; диапазон больше не будет действительным. После того, как сигнал с нарастающим фронтом 1 пс передается через межсоединение, его нарастающий фронт может составлять 0,35/8 ГГц = 0,043 нс или 43 пс, что означает, что нарастающий фронт сигнала ухудшается.
Если полоса пропускания межсоединения составляет 1 ГГц,Самый быстрый фронт, который может передавать сигнал, составляет 350 пс в секунду.,ЭтоВнутренний нарастающий фронт межсоединения. Если край Сигнал 350 пс поступает в межсоединение, так каков нарастающий фронт при его выходе? Это очень деликатный вопрос. Нарастающий фронт после выхода можно аппроксимировать следующей формулой:
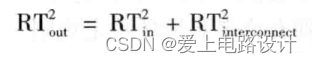
Добавьте комментарий к изображению, не более 140 слов (по желанию)
Среди них RTout представляет нарастающий фронт выходного сигнала 10–90 %, RTin представляет нарастающий фронт входного сигнала 10–90 %, а RTinterconnect представляет собственный нарастающий фронт соединения 10–90 %. Здесь предполагается, что и радиоспектр, и спектр отклика межсоединения соответствуют нарастающему фронту гауссовой формы. Например, если сигнал с нарастающим фронтом входного сигнала 50 пс передается через межсоединение длиной 4 дюйма, нарастающий фронт сигнала будет

Добавьте комментарий к изображению, не более 140 слов (по желанию)
По сравнению с нарастающим фронтом падающей волны, нарастающий фронт передаваемого сигнала увеличивается примерно на 17 пс. Ранее было введено измерение в частотной области. На рисунке 11.5.2 показаны измерения, выполненные во временной области для того же соединения длиной 4 дюйма и сопротивлением 50 Ом. Из рисунка видно, что по сравнению с формой входного сигнала форма выходного сигнала имеет сдвиг во времени от начальной точки и продолжается. Когда сигнал попадает на дорожку печатной платы, нарастающий фронт сигнала составляет 50 пс; измеренный нарастающий фронт выходного сигнала на уровне 10–90 % составляет 80 пс; Следует отметить, что измеренная форма выходного сигнала в это время имеет характеристики линии передачи с потерями и искажением с длинным хвостом наверху. Если внимательно сравнить дополнительную задержку при той же амплитуде в 70%, то она все равно составит около 15пс. Это очень близко к тому, что оценивалось ранее. Если сигнал с нарастающим фронтом 1 нс поступает в межсоединение с собственным нарастающим фронтом 0,1 нс, то нарастающий фронт после передачи равен примерно квадратному корню из (1 нс + 0,1 нс) или 1,005 нс, что по-прежнему равно 1 нс. поэтому нарастающий фронт соединения Край не имеет никакого эффекта. Однако если собственный нарастающий фронт межсоединения составляет 0,5 нс, то нарастающий фронт выхода составит 1,1 нс, и начало соединения будет иметь значительное влияние на нарастающий фронт.
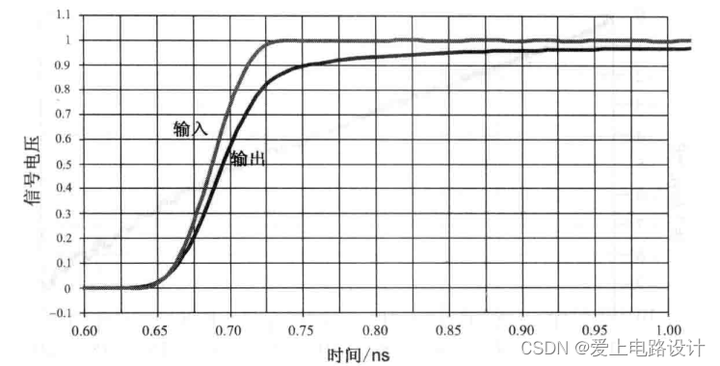
Рисунок 11.5.2 Измеренные входные сигналы и сигналы передачи через линию передачи длиной 4 дюйма с сопротивлением 50 Ом на плате FR4
Видно, что нарастающий фронт ухудшился. Нарастающий фронт входного сигнала составляет 50 пс, а нарастающий фронт выходного сигнала, рассчитанный по полосе пропускания межсоединения, составляет 67 пс. Эту картину зафиксировала зондовая станция GigaTest Labs.
Чтобы межсоединение добавляло не более 10 % к нарастающему фронту сигнала, собственный нарастающий фронт межсоединения должен составлять менее 50 % от нарастающего фронта сигнала. Это простое эмпирическое правило.
С точки зрения частотной области, чтобы лучше передавать сигналы с полосой пропускания 1 ГГц, полоса межсоединения должна быть как минимум в два раза больше полосы пропускания сигнала, то есть 2 ГГц.
Дорога длинная и долгая.,Я буду искать высоко и низко。Я думаю, это хорошо, разбогатей своими ручонками и поставь лайк!сосредоточиться Напоминаем, что в дальнейшем будет полезная информация!

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
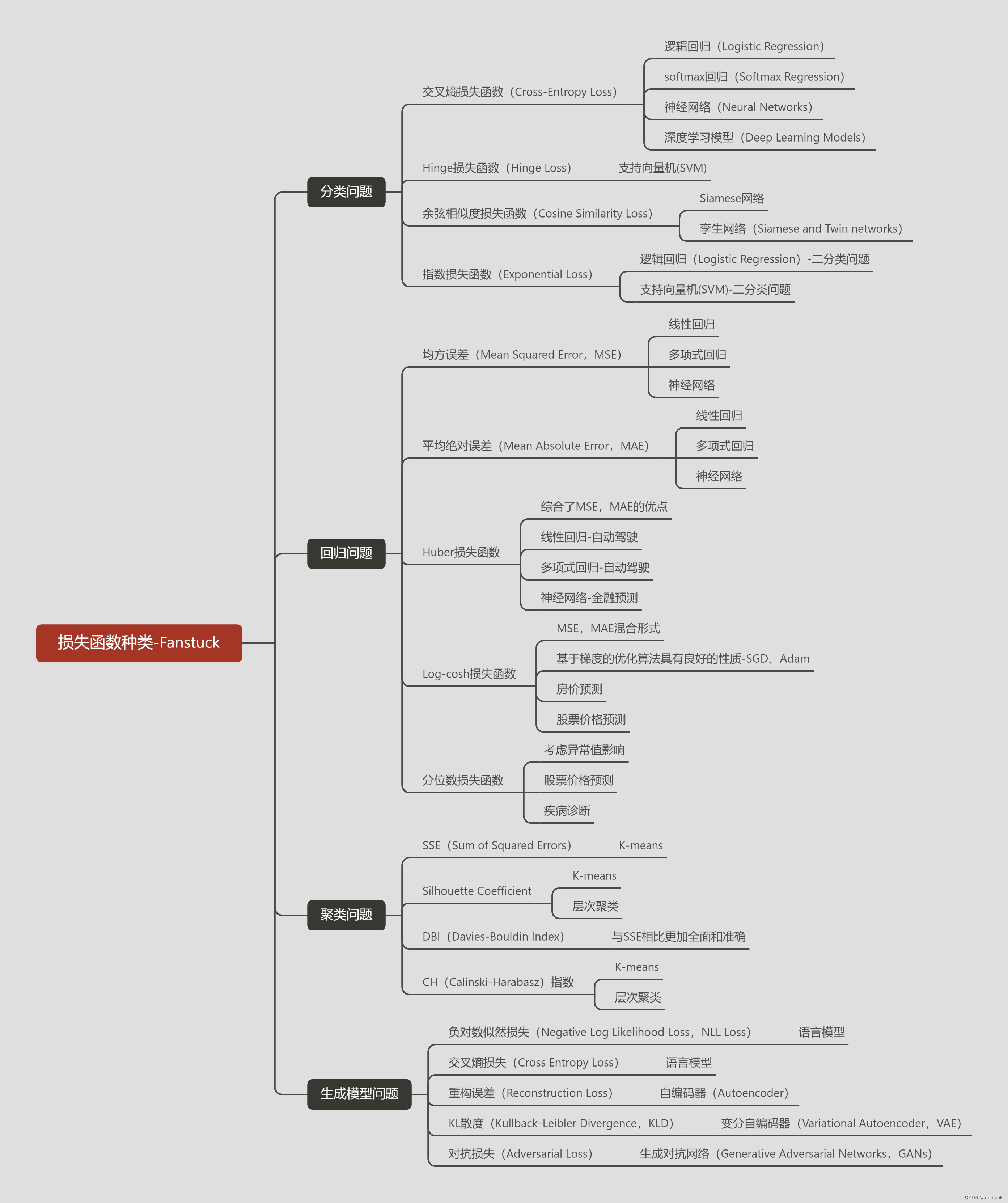
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
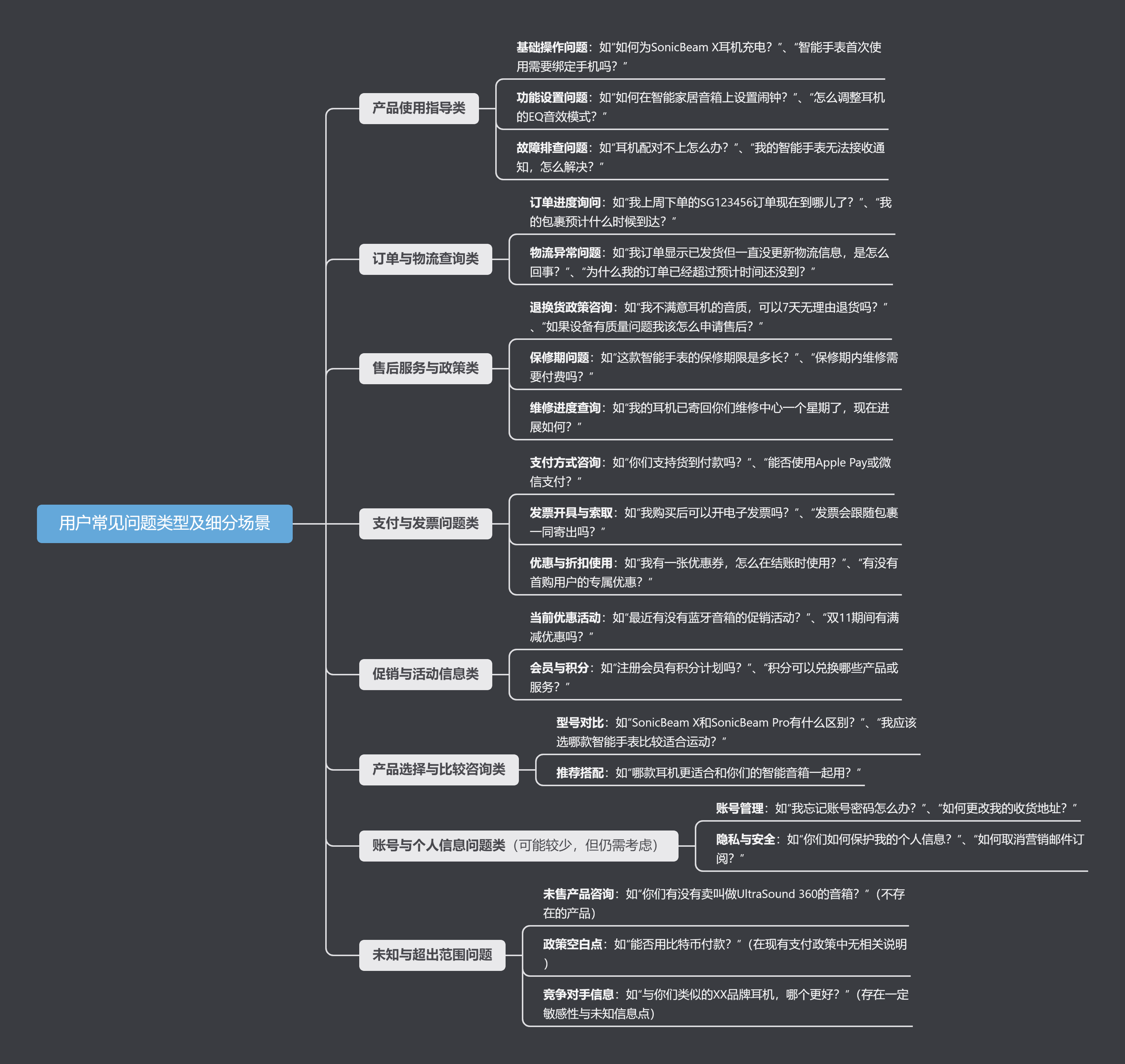
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.