MerkleTree in BTC
Дерево Меркла — это хеш-дерево, используемое для эффективной и безопасной проверки целостности и согласованности структур больших данных. Он играет жизненно важную роль в сети Биткойн. Дерево Меркла — это двоичная древовидная структура, в которой каждый листовой узел содержит хэш-значение блока данных, а каждый нелистовой узел содержит объединенный хэш хэшей своих дочерних элементов.
Дерево Меркла в сети Биткойн
В блокчейне Биткойна каждый блок содержит несколько транзакций. Для эффективной проверки транзакций внутри блока Биткойн использует деревья Меркла. Заголовок блока содержит корень Меркла, который представляет собой хеш-дайджест всех транзакций в блоке.
Построение деревьев Меркла
- листовой узел:за транзакциюхэшзначение используется каклистовой узел。
- Нетлистовой узел:за парулистовой Значения узлахэш объединяются и хэшируются для формирования узла верхнего уровня. Этот процесс протекает рекурсивно до тех пор, пока не будет сформирован уникальный корневой узел, т.е. Merkle корень.
Пример создания дерева Меркла
Предположим, что блок содержит четыре транзакции. T1 、T2 、T3 и T4 . генерировать Merkle Шаги для дерева следующие:
- Рассчитайте хэш-значение каждой транзакции H1 、H2 、H3 、H4 :
- Вычислить объединенный хэш соседних хешей транзакций H12 и H34 :
- Вычислить хеш корневого узла H1234 :
финальный,H1234 Он включает в себя эти четыре транзакции Merkle корень.
Роль деревьев Меркла
- Подтвердить транзакцию:проходить Merkle Дерево,Может эффективно проверять, включена ли транзакция в определенный блок,без проверки всего блока.
- Легкий клиент (SPV):Упростите проверку платежа(SPV)Клиент можетпроходить Запросить заголовок блокаитребуемая транзакция Merkle путь к Подтвердить транзакцию без загрузки всего блокчейна.
Проверка пути Меркла
Предположим, мы хотим проверить, находится ли транзакция $T3$ в определенном блоке:
- Получить транзакцию $T3$ хэш H3 。
- получать $H3$ соседний хэш H4 。
- Вычислить комбинированный хэш H34 = \text{Hash}(H3 || H4) 。
- получать H34 соседний хэш H12 。
- Вычислить хеш корневого узла H1234 = \text{Hash}(H12 || H34) И с заголовком блока Merkle Корневое сравнение.
Если вычисленный корневой хэш соответствует корню Меркла в заголовке блока, проверка успешна, что указывает на то, что транзакция $T3$ включена в блок.
Реализация дерева Меркла в btcd
существовать btcd В, Меркл Дерево Реализация главногосуществовать blockchain/merkle.go в файле. Вот подробное описание ключевых разделов файла:
// HashMerkleBranches Принимает два хэш-значения, рассматриваемых как левый узел Дерева и правый узел Дерева соответственно, и возвращает их объединенное значение хэш. Используется для создания Дерева Меркеля.
func HashMerkleBranches(left, right *chainhash.Hash) chainhash.Hash {
// Concatenate the left and right nodes.
var hash [chainhash.HashSize * 2]byte
copy(hash[:chainhash.HashSize], left[:])
copy(hash[chainhash.HashSize:], right[:])
return chainhash.DoubleHashRaw(func(w io.Writer) error {
_, err := w.Write(hash[:])
return err
})
}
// BuildMerkleTreeStore creates a merkle tree from a slice of transactions,
// stores it using a linear array, and returns a slice of the backing array. A
// linear array was chosen as opposed to an actual tree structure since it uses
// about half as much memory. The following describes a merkle tree and how it
// is stored in a linear array.
func BuildMerkleTreeStore(transactions []*btcutil.Tx, witness bool) []*chainhash.Hash {
// Calculate how many entries are required to hold the binary merkle
// tree as a linear array and create an array of that size.
nextPoT := nextPowerOfTwo(len(transactions))
arraySize := nextPoT*2 - 1
merkles := make([]*chainhash.Hash, arraySize)
// Create the base transaction hashes and populate the array with them.
for i, tx := range transactions {
// If we're computing a witness merkle root, instead of the
// regular txid, we use the modified wtxid which includes a
// transaction's witness data within the digest. Additionally,
// the coinbase's wtxid is all zeroes.
switch {
case witness && i == 0:
var zeroHash chainhash.Hash
merkles[i] = &zeroHash
case witness:
wSha := tx.MsgTx().WitnessHash()
merkles[i] = &wSha
default:
merkles[i] = tx.Hash()
}
}
// Start the array offset after the last transaction and adjusted to the
// next power of two.
offset := nextPoT
for i := 0; i < arraySize-1; i += 2 {
switch {
// When there is no left child node, the parent is nil too.
case merkles[i] == nil:
merkles[offset] = nil
// When there is no right child, the parent is generated by
// hashing the concatenation of the left child with itself.
case merkles[i+1] == nil:
newHash := HashMerkleBranches(merkles[i], merkles[i])
merkles[offset] = &newHash
// The normal case sets the parent node to the double sha256
// of the concatenation of the left and right children.
default:
newHash := HashMerkleBranches(merkles[i], merkles[i+1])
merkles[offset] = &newHash
}
offset++
}
return merkles
}BuildMerkleTreeStore Создать Дерево Меркеля из среза транзакции,Сохраните его, используя линейный массив,и возвращает фрагмент массива, поддерживаемого массивом. Выберите линейный массив вместо фактической структуры Дерева.,Потому что это может сэкономить около половины памяти. Ниже описывается Дерево Меркла и то, как оно хранится в существующем линейном массиве.
root = h1234 = h(h12 + h34)
/ \
h12 = h(h1 + h2) h34 = h(h3 + h4)
/ \ / \
h1 = h(tx1) h2 = h(tx2) h3 = h(tx3) h4 = h(tx4)Вышеупомянутое сохраняется в виде линейного массива следующим образом:
[h1 h2 h3 h4 h12 h34 root]Как показано выше, корень Меркла всегда является последним элементом массива.

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
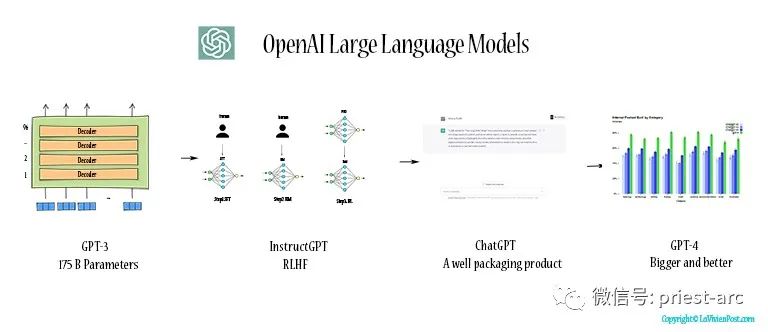
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
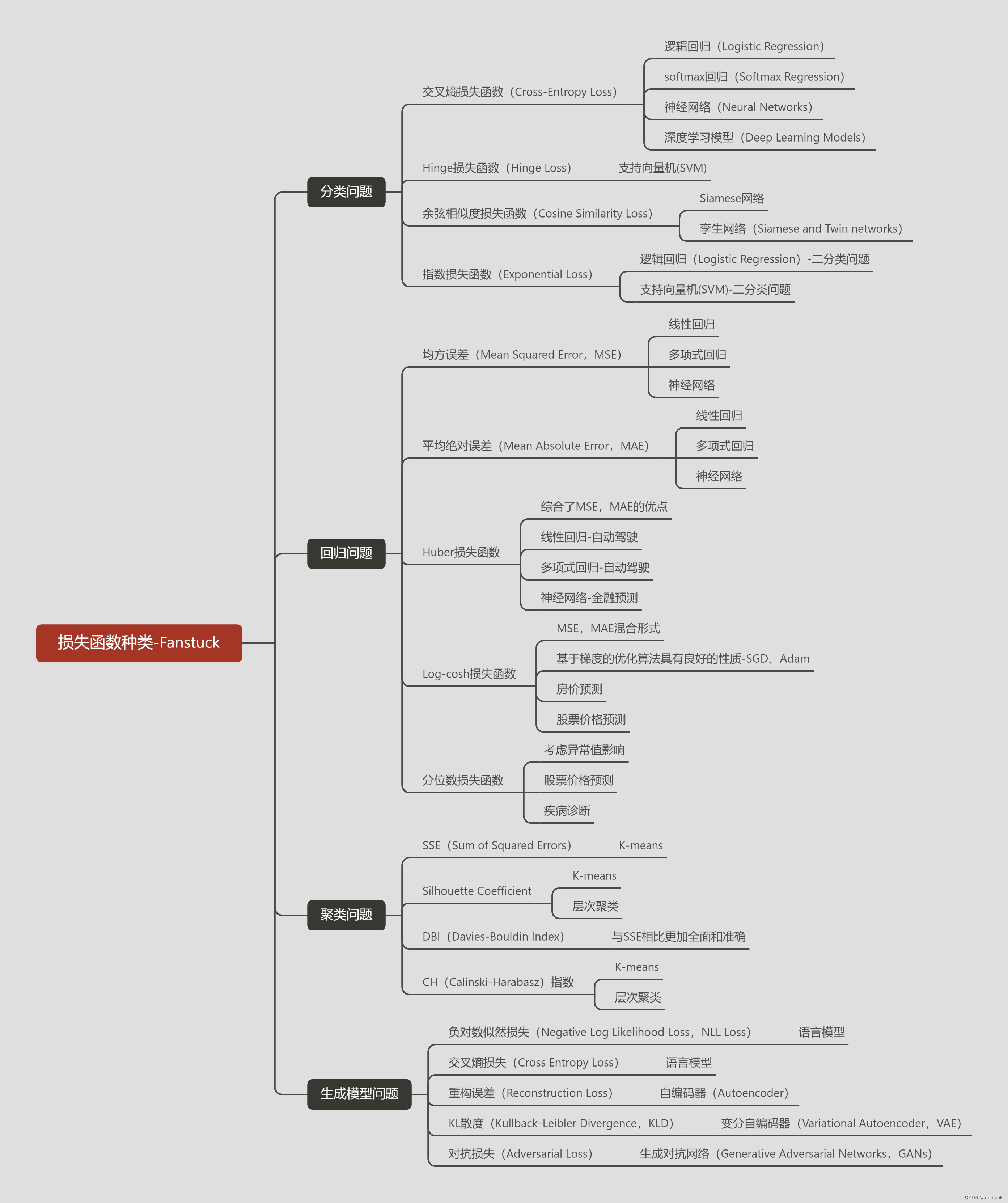
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
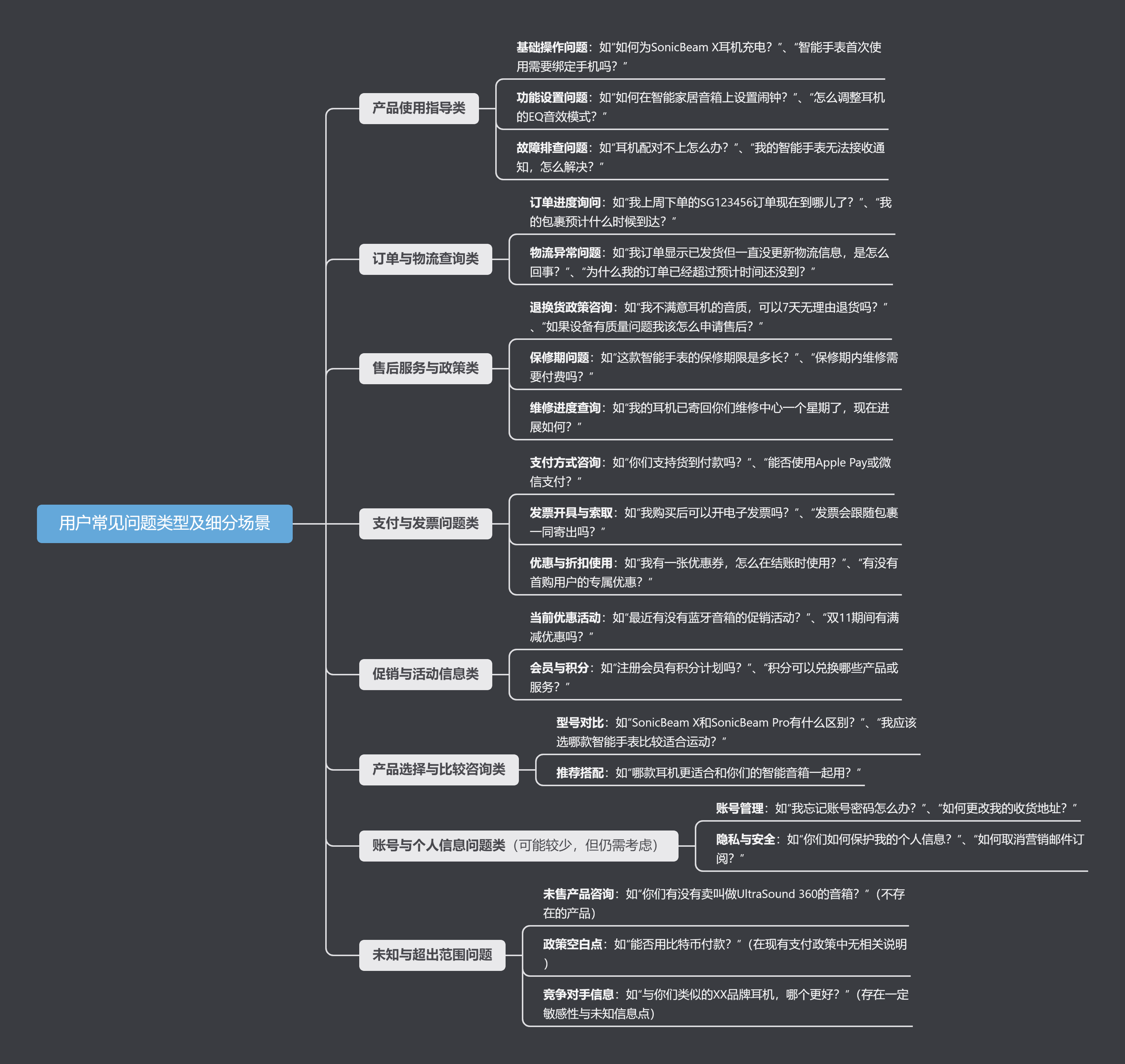
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
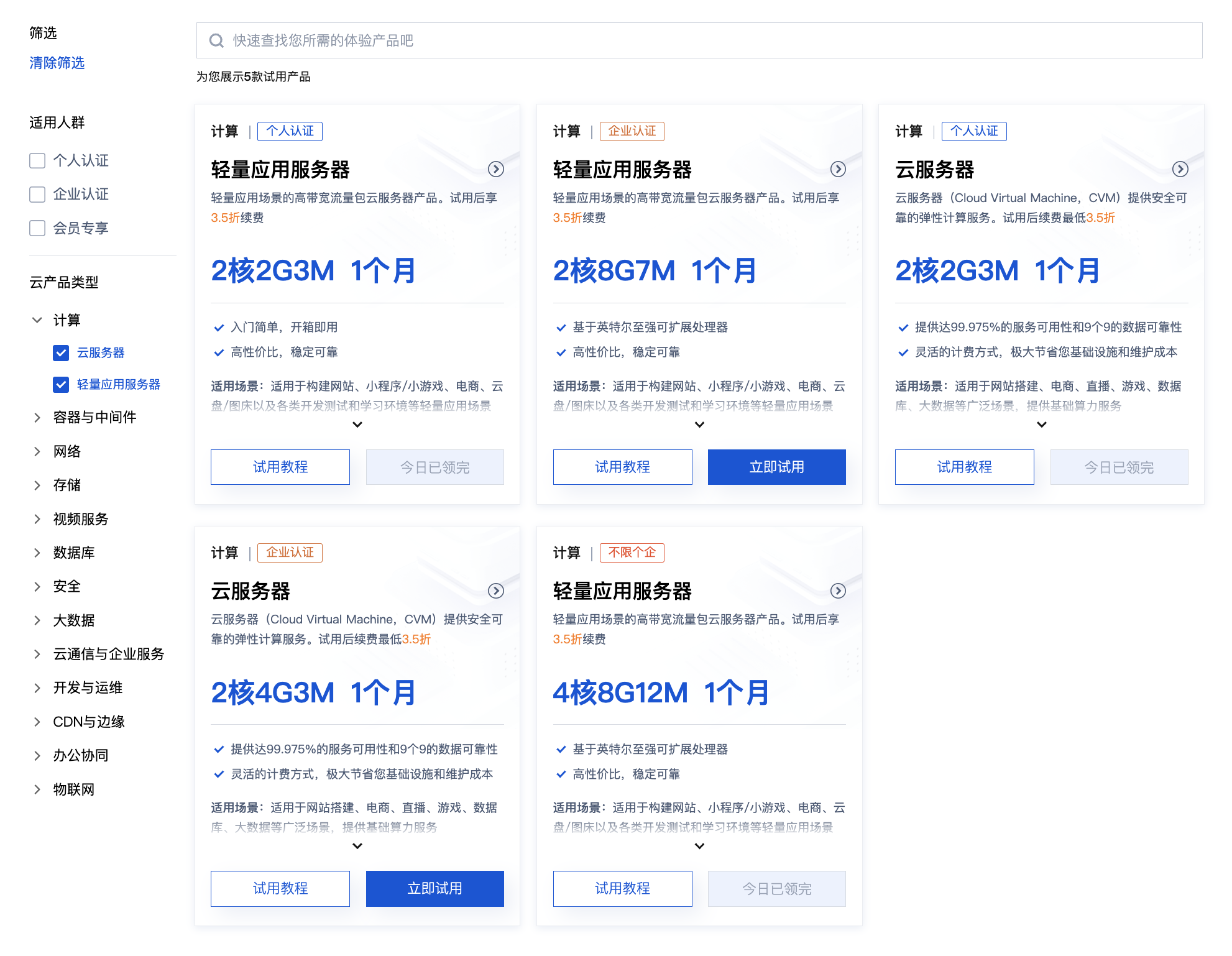
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.