Математическое моделирование - совместная оптимизация доставки сельского общественного транспорта и гетерогенных дронов
Математическое моделирование - совместная оптимизация доставки сельского общественного транспорта и гетерогенных дронов

1. Вопрос

Вопрос А: Сельский общественный транспорт и оптимизация совместной доставки гетерогенных БПЛА

Из-за сложной и изменчивой местности, разреженной дорожной сети и разбросанных пунктов распределения в сельской местности традиционные методы распределения неэффективны и дорогостоящи, что затрудняет удовлетворение растущего спроса на распределение. Благодаря быстрому развитию технологий дронов и их широкому применению в сфере логистики появилась новая модель доставки — совместная модель доставки между сельскими автобусами и разнородными дронами.

Являясь важной частью системы наземного транспорта, сельский общественный транспорт имеет широкую зону покрытия, работает в фиксированное время и имеет относительно низкие затраты, обеспечивая идеальную наземную поддержку для дронов. Объединив дроны с сельским общественным транспортом, можно в полной мере использовать преимущества обоих для достижения эффективной совместной доставки. В частности, сельские автобусы отвечают за доставку дронов и товаров на различные автостанции. Эти станции являются не только точками взлета и посадки дронов, но и центрами перевалки товаров. Дроны пользуются своим превосходством в воздухе, чтобы взлетать с автобусных остановок и быстро и точно выполнять задачи по доставке в конкретные точки доставки.

Для повышения эффективности и гибкости распределения особенно важно использование гетерогенных дронов. Гетерогенные БПЛА имеют разные летные характеристики, грузоподъемность и скорость и могут гибко распределять задачи в соответствии с различными потребностями доставки. Рационально подбирая и распределяя различные типы гетерогенных дронов, можно точно реагировать на сложные и меняющиеся потребности в дистрибуции и повышать общую эффективность дистрибуции.

Внедрение услуг одновременного вывоза и доставки также может лучше отражать уникальные потребности сельской логистики. За один полет дроны могут выполнять задачи по доставке и сбору товаров в нескольких точках распределения, тем самым значительно повышая эффективность распределения и сокращая время выполнения работ. Тщательно планируя траектории полетов и рационально распределяя задачи, можно эффективно сократить количество используемых дронов и частоту полетов.

Сельские автобусы загружают товары и дроны, отправляются из распределительного центра и едут по фиксированным автобусным маршрутам и автобусным остановкам. Точно распределяйте типы дронов и задачи доставки на основе потребностей клиентов и производительности дронов. Дрон взлетает на автобусной остановке рядом с точкой клиента и выполняет задачи по сбору и доставке по оптимизированному маршруту для обеспечения эффективного выполнения заказов. После завершения миссии дрон возвращается на ближайшую площадку, садится на следующий автобус, проезжающий мимо площадки, выполняет быструю замену батареи, а затем продолжает обслуживать точки спроса клиентов рядом с площадкой или отправляет автобус на другие площадки для обслуживания окружающего спроса. Очки После того, как у дрона нет миссии, сядьте на автобус обратно в распределительный центр. На протяжении всего процесса дроны тесно взаимодействовали с сельскими автобусами, циклически выполняя задачи по доставке, пока все задачи не были выполнены. Благодаря этой модели мы можем в полной мере использовать преимущества земли и воздуха, повысить эффективность распределения, снизить затраты и удовлетворить растущие потребности в распределении в сельской местности.

Предположим, что дрон может дождаться следующего автобуса на автобусной остановке. Если на автобусной остановке есть возвращающийся дрон, который необходимо загрузить, автобус останется на остановке в течение 5 минут для замены аккумулятора дрона (зарядка не производится). требуется) ) и погрузка груза. Стоимость дронов состоит из двух частей: одна — это фиксированная стоимость, которая будет возникать в течение всего периода использования и зависит от типа дрона. Другая — стоимость транспортировки, которая зависит от типа дрона и модели. пробег в процессе транспортировки (от вылета до места) в милях, доставленных обратно на объект. Кроме того, задачи в точке спроса не могут быть разделены. Автобус может перевозить до двух дронов. После выполнения ежедневного задания дрон должен вернуться на исходную станцию. Временное окно точки заказчика и случайность. дорога не учтена. Имеется пробка, автобус едет со скоростью 35 км/ч.

Решите, пожалуйста, следующие вопросы, опираясь на данные во вложении:

Вопрос 1 Рассматриваются только дроны класса А. Предоставьте план совместной доставки общественного транспорта и дронов, чтобы минимизировать общую стоимость. Укажите конкретные маршруты и расписание рейсов.

Вопрос 2 Если можно использовать все три типа дронов, предоставьте план совместной доставки с наименьшими затратами.

Вопрос 3 существовать Вопрос 2на основе,Если есть необходимость забрать товар в каждой точке спроса,И вы можете получить определенный доход от самовывоза товара (0,5 юаня за килограмм),Пожалуйста, предоставьте лучший план доставки.

2. Вопрос 1

Рассматриваются только дроны класса А. Предоставьте план совместной доставки автобусов и дронов, чтобы минимизировать общую стоимость.

1. Моделирование проблем

Введите данные

  • данные автобусной остановки：Укажите расположение объектов и расстояние между ними.。
  • Данные точки спроса: включая местоположение точки спроса и требования к распределению.
  • Параметры производительности БПЛА класса А: включая максимальную дальность полета, грузоподъемность, фиксированную плату и плату за полет.
  • Расписание автобусов: время отправления и прибытия автобусов.

2. Выбор алгоритма

3. Импорт данных

Язык кода:javascript
копировать
# данные автобусной остановки
stations_data = pd.DataFrame({
    'Station_ID': [1, 2, 3, 4, 5, 6, 7, 8, 9],
    'Longitude': [110.125713, 110.08442, 110.029866, 109.962839, 109.956003, 109.920425, 109.839046, 109.823329, 109.767127],
    'Latitude': [32.815024, 32.771676, 32.748994, 32.743622, 32.812194, 32.856136, 32.860495, 32.847468,32.807855]
})

# точка спросаданные
demands_data = pd.DataFrame({
    'Demand_ID': range(1, 51),
    'Longitude': [
        110.1053385, 110.1147032, 110.0862574, 110.0435344, 110.0575508,
        110.0386243, 110.0115086, 110.0390602, 110.0246454, 110.0575847,
        109.9456331, 109.9612274, 109.94592, 109.9316682, 109.9245376,
        109.7087533, 109.7748005, 109.7475891, 109.7534532, 109.783015,
        109.7410728, 109.7554844, 109.7147417, 109.8807093, 109.8070677,
        109.9054481, 109.8954509, 109.8979229, 109.8942179, 109.8610985,
        109.8744682, 109.8338804, 109.870924, 109.8292467, 109.8711312,
        109.8813363, 109.978788, 109.8166563, 109.8151216, 109.885638,
        109.9890984, 109.9647812, 109.9303732, 109.9401099, 109.944496,
        109.979708, 109.976757, 109.94999, 109.973673, 109.967765
    ],
     'Latitude': [
        32.77881526, 32.75599834, 32.74905239, 32.74275416, 32.76712584,
        32.70855831, 32.72619993, 32.73965997, 32.72360718, 32.76553658,
        32.7526657, 32.72286471, 32.70899877, 32.73848444, 32.70740885,
        32.7815564, 32.80016336, 32.80903496, 32.85129032, 32.82296929,
        32.82914197, 32.80581363, 32.79995734, 32.89696579, 32.79622985,
        32.89437141, 32.86724756, 32.83444574, 32.83224374, 32.90687042,
        32.89939698, 32.85616627, 32.848223, 32.83825122, 32.88979101,
        32.8642824, 32.75943454, 32.8096699, 32.82822489, 32.84032485,
        32.80854774, 32.80993619, 32.78956582, 32.85264625, 32.802178,
        32.817449, 32.811064, 32.795207, 32.746858, 32.820998
    ],
    'Demand_kg': [3, 4, 2, 0, 8, 7, 4, 9, 10, 6, 7, 12, 3, 5, 6, 5, 3, 13, 12, 3,
                  14, 10, 4, 34, 6, 6, 3, 4, 20, 5, 6, 5, 3, 15, 2, 6, 3, 4, 3, 2,
                  6, 5, 9, 3, 3, 4, 6, 4, 4, 0]
})
# Параметры БПЛА
D_max = 27  # Максимальная дальность полета
Q_max = 9   # Максимальная нагрузка
C_fixed = 80  # фиксированная плата
C_per_km = 0.8  # стоимость за километр
wait_time = 5 / 60  # Время ожидания (часы)
battery_swap_time = 5 / 60  # Время замены батареи (часы)

# Параметры шины
bus_speed = 35  # Скорость автобуса (км/ч)
bus_schedule = {
    «Байхэ — Цаншан»: [6.67, 8.5, 9, 11, 14, 16.5],
    «Цаншан — Байхэ»: [6, 7.33, 8.83, 11, 14, 15.83]
}

3. Построение модели

import pandas as pd # Данные автовокзала Station_data = pd.DataFrame({ 'Station_ID': [1, 2, 3, 4, 5, 6, 7, 8, 9], 'Longitude': [110.125713, 110.08442, 110.029866, 109.962839, 109.956003, 109.920425, 109.839046, 109.823329, 109.767127], 'Широта': [32.815024, 32.771676, 32.748994, 32.743622, 32.812194, 32.856136, 32.860495, 32.847468, 32.807855] }) # Данные точки спроса require_data = pd.DataFrame({ 'Demand_ID': range(1, 51), 'Longitude': [ 110.1053385, 110.1147032, 110.0862574, 110.0435344, 110.0575508, 110.0386243, 110.0115086, 110.0390602, 110.0246454, 110.0575847, 109.9456331, 109.9612274, 109.94592, 109.9316682, 109.9245376, 109.7087533, 109.7748005, 109.7475891, 109.7534532, 109.783015, 109.7410728, 109.7554844, 109.7147417, 109.8807093, 109.8070677, 109.9054481, 109.8954509, 109.8979229, 109.8942179, 109.8610985, 109.8744682, 109.8338804, 109.870924, 109.8292467, 109.8711312, 109.8813363, 109.978788, 109.8166563, 109.8151216, 109.885638, 109.9890984, 109.9647812, 109.9303732, 109.9401099, 109.944496, 109.979708, 109.976757, 109.94999, 109.973673, 109.967765 ], 'Широта': [ 32.77881526, 32.75599834, 32.74905239, 32.74275416, 32.76712584, 32.70855831, 32.72619993, 32.73965997, 32.72360718, 32.76553658, 32.7526657, 32.72286471, 32.70899877, 32.73848444, 32.70740885, 32.7815564, 32.80016336, 32.80903496, 32.85129032, 32.82296929, 32.82914197, 32.80581363, 32.79995734, 32.89696579, 32.79622985, 32.89437141, 32.86724756, 32.83444574, 32.83224374, 32.90687042, 32.89939698, 32.85616627, 32.848223, 32.83825122, 32.88979101, 32.8642824, 32.75943454, 32.8096699, 32.82822489, 32.84032485, 32.80854774, 32.80993619, 32.78956582, 32.85264625, 32.802178, 32.817449, 32.811064, 32.795207, 32.746858, 32.820998 ], 'Спрос_кг': [3, 4, 2, 0, 8, 7, 4, 9, 10, 6, 7, 12, 3, 5, 6, 5, 3, 13, 12, 3, 14, 10 , 4, 34, 6, 6, 3, 4, 20, 5, 6, 5, 3, 15, 2, 6, 3, 4, 3, 2, 6, 5, 9, 3, 3, 4, 6, 4, 4, 0] })stations_data.head(), require_data.head()

результат

Язык кода:javascript
копировать
(   Station_ID   Longitude   Latitude
 0           1  110.125713  32.815024
 1           2  110.084420  32.771676
 2           3  110.029866  32.748994
 3           4  109.962839  32.743622
 4           5  109.956003  32.812194,
    Demand_ID   Longitude   Latitude  Demand_kg
 0          1  110.105339  32.778815          3
 1          2  110.114703  32.755998          4
 2          3  110.086257  32.749052          2
 3          4  110.043534  32.742754          0
 4          5  110.057551  32.767126          8)

Мы загрузили данные по автобусным остановкам и точкам спроса. Далее мы рассчитаем расстояние между каждой станцией и точкой спроса на основе этих данных и создадим модель оптимизации для решения оптимального плана совместной доставки между общественным транспортом и дронами класса А.

1. Расчет расстояния

Во-первых, нам нужно рассчитать расстояние между каждым объектом и каждой точкой спроса.

2. Оптимизировать модель

Для решения этой проблемы мы будем использовать целочисленное линейное программирование (ILP). Цель состоит в том, чтобы минимизировать общие затраты, включая фиксированные расходы и летные расходы.

конкретные шаги
  1. Вычислите матрицу расстояний.
  2. Учреждатьоптимизация Модель。
  3. Решать Модель,Получите оптимальный путь и график.

Дальнейшая оптимизация

  1. Учитывайте время ожидания дрона и время замены батареи.：Зависит Возможно, дрону придется дождаться автобуса или выполнить замену аккумулятора на месте.,Эти времена также необходимо учитывать в оптимизации Модели.
  2. Учитывайте расписание автобусов：оптимизация Модель Необходимо совместить со временем отправления автобуса.,Чтобы гарантировать, что дрон сможет выполнить свою миссию в разумные сроки.
  3. Рассмотрите возможность совместной работы нескольких дронов：Каждый автобус может перевозить до двух дронов.,Необходимо обеспечить правильное распределение задач этих дронов.

Ниже приведен более подробный и оптимизированный этап реализации:

1. Переопределите проблему

Переформулируйте задачу, учитывая время ожидания, время замены батарей и расписание автобусов.

2. Определение переменной
3. Цели оптимизации

Минимизируйте общие затраты, включая фиксированные расходы, расходы на перелет, время ожидания и время замены аккумулятора.

конкретные шаги
  1. Вычислите матрицу расстояний.
  2. Учреждатьоптимизация Модель。
  3. Решать Модель,Получите оптимальный путь и график.

Ниже приводится конкретная реализация:

Язык кода:javascript
копировать
import numpy as np
from geopy.distance import geodesic
import pulp

# Вычислить матрицу расстояний
num_stations = stations_data.shape[0]
num_demands = demands_data.shape[0]

distances = np.zeros((num_stations, num_demands))
for i, station in stations_data.iterrows():
    for j, demand in demands_data.iterrows():
        distances[i, j] = geodesic((station['Latitude'], station['Longitude']), (demand['Latitude'], demand['Longitude'])).km

# Параметры БПЛА
D_max = 27  # Максимальная дальность полета
Q_max = 9   # Максимальная нагрузка
C_fixed = 80  # фиксированная плата
C_per_km = 0.8  # стоимость за километр
wait_time = 5 / 60  # Время ожидания (часы)

# Параметры шины
bus_speed = 35  # Скорость автобуса (км/ч)
bus_schedule = {
    «Байхэ — Цаншан»: [6.67, 8.5, 9, 11, 14, 16.5],
    «Цаншан — Байхэ»: [6, 7.33, 8.83, 11, 14, 15.83]
}

# Создать вопрос по оптимизации
prob = pulp.LpProblem("Minimize_Cost", pulp.LpMinimize)

# Определите переменные решения
x = pulp.LpVariable.dicts("x", (range(num_stations), range(num_demands)), cat='Binary')
t = pulp.LpVariable.dicts("t", (range(num_stations), range(num_demands)), lowBound=0)

# целевая функция
prob += pulp.lpSum(x[i][j] * (C_fixed + distances[i, j] * C_per_km + wait_time * bus_speed) for i in range(num_stations) for j in range(num_demands))

# Ограничения
for j in range(num_demands):
    prob += pulp.lpSum(x[i][j] for i in range(num_stations)) == 1  # Каждая точка спроса может быть доставлена ​​только одним дроном.

for i in range(num_stations):
    for j in range(num_demands):
        prob += distances[i, j] * x[i][j] <= D_max  # Ограничение дальности полета дрона
        prob += demands_data.loc[j, 'Demand_kg'] * x[i][j] <= Q_max  # Ограничение по весу дрона

# Ограничения на поездки на автобусе
for schedule in bus_schedule.values():
    for i in range(1, len(schedule)):
        prob += (schedule[i] - schedule[i-1]) * bus_speed >= 0

# решать проблемы
prob.solve()

# анализироватьрезультат
optimal_routes = []
for i in range(num_stations):
    for j in range(num_demands):
        if pulp.value(x[i][j]) == 1:
            optimal_routes.append((i+1, j+1, distances[i, j]))

optimal_routes

Снова Дальнейшая оптимизация

  1. Время отправления и прибытия автобуса：Убедитесь, что время начала и окончания миссии дронов соответствует расписанию автобусов.。
  2. Замена батареи и время загрузки：Включите время на замену аккумулятора дрона и погрузку груза.Модель。
  3. Распределение задач для нескольких дронов：Разумно распределяйте задачи между несколькими дронами,Убедитесь, что в каждом автобусе находится не более двух дронов.
Конкретные этапы реализации
1. Рассчитать матрицу расстояний

Сначала рассчитайте расстояние между каждым объектом и каждой точкой спроса.

2. Определение переменной
3. Ограничения
  • В каждую точку спроса может быть доставлен только один дрон.
  • Максимальное расстояние полета дрона.
  • Ограничения грузоподъемности БПЛА.
  • Время отправления и прибытия автобусов.
4. Цели оптимизации

Минимизируйте общие затраты, включая фиксированные расходы, расходы на перелет, время ожидания и время замены аккумулятора.

Ниже приводится конкретная реализация модели оптимизации:

Сначала мы переопределяем и решаем оптимизационную модель,

1. Убедитесь, что все ограничения и целевые функции реализованы правильно.
Язык кода:javascript
копировать
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

# Установите путь к китайскому шрифту (пожалуйста, измените путь в соответствии с реальной ситуацией)
font_path = 'C:/Windows/Fonts/simhei.ttf'  # Пожалуйста, замените фактический путь к шрифту
font = FontProperties(fname=font_path)

# Обновить информацию о дроне
D_max_A = 27  # Максимальная дальность полета (km)
Q_max_A = 9  # Максимальная нагрузка (kg)
C_fixed_A = 80  # фиксированная плата (юань/день)
C_per_km_A = 0.8  # стоимость за километр (юань/км)
drone_speed = 16.7 / 3.6  # Скорость дрона (km/h), Зависит от m/s конвертировать в km/h

# данные автобусной остановки
stations_data = pd.DataFrame({
    'Station_ID': [1, 2, 3, 4, 5, 6, 7, 8, 9],
    'Longitude': [110.125713, 110.08442, 110.029866, 109.962839, 109.956003, 109.920425, 109.839046, 109.823329, 109.767127],
    'Latitude': [32.815024, 32.771676, 32.748994, 32.743622, 32.812194, 32.856136, 32.860495, 32.847468,32.807855]
})

# точка спросаданные
demands_data = pd.DataFrame({
    'Demand_ID': range(1, 51),
    'Longitude': [
        110.1053385, 110.1147032, 110.0862574, 110.0435344, 110.0575508,
        110.0386243, 110.0115086, 110.0390602, 110.0246454, 110.0575847,
        109.9456331, 109.9612274, 109.94592, 109.9316682, 109.9245376,
        109.7087533, 109.7748005, 109.7475891, 109.7534532, 109.783015,
        109.7410728, 109.7554844, 109.7147417, 109.8807093, 109.8070677,
        109.9054481, 109.8954509, 109.8979229, 109.8942179, 109.8610985,
        109.8744682, 109.8338804, 109.870924, 109.8292467, 109.8711312,
        109.8813363, 109.978788, 109.8166563, 109.8151216, 109.885638,
        109.9890984, 109.9647812, 109.9303732, 109.9401099, 109.944496,
        109.979708, 109.976757, 109.94999, 109.973673, 109.967765
    ],
    'Latitude': [
        32.77881526, 32.75599834, 32.74905239, 32.74275416, 32.76712584,
        32.70855831, 32.72619993, 32.73965997, 32.72360718, 32.76553658,
        32.7526657, 32.72286471, 32.70899877, 32.73848444, 32.70740885,
        32.7815564, 32.80016336, 32.80903496, 32.85129032, 32.82296929,
        32.82914197, 32.80581363, 32.79995734, 32.89696579, 32.79622985,
        32.89437141, 32.86724756, 32.83444574, 32.83224374, 32.90687042,
        32.89939698, 32.85616627, 32.848223, 32.83825122, 32.88979101,
        32.8642824, 32.75943454, 32.8096699, 32.82822489, 32.84032485,
        32.80854774, 32.80993619, 32.78956582, 32.85264625, 32.802178,
        32.817449, 32.811064, 32.795207, 32.746858, 32.820998
    ],
    'Demand_kg': [3, 4, 2, 0, 8, 7, 4, 9, 10, 6, 7, 12, 3, 5, 6, 5, 3, 13, 12, 3,
                  14, 10, 4, 34, 6, 6, 3, 4, 20, 5, 6, 5, 3, 15, 2, 6, 3, 4, 3, 2,
                  6, 5, 9, 3, 3, 4, 6, 4, 4, 0]
})

# Вычислить расстояние между двумя точками (формула Хаверсина)
def haversine(lon1, lat1, lon2, lat2):
    lon1, lat1, lon2, lat2 = map(np.radians, [lon1, lat1, lon2, lat2])
    dlon = lon2 - lon1
    dlat = lat2 - lat1
    a = np.sin(dlat / 2) ** 2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon / 2) ** 2
    c = 2 * np.arcsin(np.sqrt(a))
    r = 6371  # Средний радиус Земли (км)
    return c * r

# Преобразуйте широту и долготу автобусных остановок и точек спроса в массивы NumPy.
stations_lons = stations_data['Longitude'].values
stations_lats = stations_data['Latitude'].values
demands_lons = demands_data['Longitude'].values
demands_lats = demands_data['Latitude'].values

# Используйте механизм трансляции для расчета расстояний от всех автобусных остановок до всех точек спроса.
stations_lons_matrix, demands_lons_matrix = np.meshgrid(stations_lons, demands_lons)
stations_lats_matrix, demands_lats_matrix = np.meshgrid(stations_lats, demands_lats)
distances_matrix = haversine(stations_lons_matrix, stations_lats_matrix, demands_lons_matrix, demands_lats_matrix)

# Преобразование матрицы расстояний в форму словаря
distances = {(stations_data['Station_ID'][i], demands_data['Demand_ID'][j]): distances_matrix[j, i]
             for i in range(len(stations_data)) for j in range(len(demands_data))}

# Расписание отправлений
bus_schedule = {
    «Байхэ — Цаншан»: [6.67, 8.5, 9, 11, 14, 16.5],
    «Цаншан — Байхэ»: [6, 7.33, 8.83, 11, 14, 15.83]
}

# Назначайте задачи и рассчитывайте общие затраты, чтобы каждая точка спроса обслуживалась только один раз.
def allocate_tasks_and_calculate_costs():
    total_cost = 0
    task_allocation = []
    demand_visited = set()

    for demand_id, demand in demands_data.iterrows():
        if demand['Demand_kg'] > Q_max_A:
            continue

        best_cost = float('inf')
        best_station = None

        # Найти ближайший сайт
        for station_id, station in stations_data.iterrows():
            station_id = station['Station_ID']
            distance = distances[(station_id, demand['Demand_ID'])]
            if distance <= D_max_A:
                cost = C_fixed_A + 2 * distance * C_per_km_A  # Расстояние туда и обратно
                if cost < best_cost:
                    best_cost = cost
                    best_station = station_id

        if best_station is not None and demand['Demand_ID'] not in demand_visited:
            total_cost += best_cost
            task_allocation.append((demand['Demand_ID'], best_station, best_cost))
            demand_visited.add(demand['Demand_ID'])

    return total_cost, task_allocation

total_cost, task_allocation = allocate_tasks_and_calculate_costs()

# Создавайте конкретные маршруты и расписания рейсов
def generate_flight_schedule():
    wait_time = 5 / 60  # Время ожидания (часы)
    flight_schedule = []

    for direction, times in bus_schedule.items():
        for time in times:
            for task in task_allocation:
                demand_id, station_id, cost = task
                arrival_time = time
                distance = distances[(station_id, demand_id)]
                flight_time = distance / drone_speed  # Рассчитайте время полета на основе новой скорости полета.
                start_time = arrival_time + wait_time
                end_time = start_time + flight_time

                flight_schedule.append({
                    'Direction': direction,
                    'Bus_Arrival_Time': arrival_time,
                    'Demand_ID': demand_id,
                    'Station_ID': station_id,
                    'Flight_Start_Time': start_time,
                    'Flight_End_Time': end_time,
                    'Cost': cost
                })

    return flight_schedule

flight_schedule = generate_flight_schedule()

# Визуализируйте траекторию полета
def visualize_flight_paths():
    fig, ax = plt.subplots()

    # Нарисуйте автобусные остановки
    ax.scatter(stations_data['Longitude'], stations_data['Latitude'], c='blue', label='автобусная остановка')

    # Нарисуйте точки спроса
    ax.scatter(demands_data['Longitude'], demands_data['Latitude'], c='red', label='точка спроса')

    # Нарисовать траекторию полета
    for task in flight_schedule:  # показать все пути
        demand = demands_data.loc[demands_data['Demand_ID'] == task['Demand_ID']].iloc[0]
        station = stations_data.loc[stations_data['Station_ID'] == task['Station_ID']].iloc[0]
        ax.plot([station['Longitude'], demand['Longitude']], [station['Latitude'], demand['Latitude']], c='green')

    ax.legend(prop=font)
    ax.set_xlabel('Долгота', fontproperties=font)
    ax.set_ylabel('Широта', fontproperties=font)
    ax.set_title('Траектория полета', fontproperties=font)
    plt.show()

visualize_flight_paths()

print(f"Минимальная общая стоимость: {total_cost:.2f} юань")
print("Путь и расписание полета:")
visited_demands = set()
for flight in flight_schedule:  # распечатать все пути
    if flight['Demand_ID'] not in visited_demands:
        print(f"Направление: {flight['Direction']}, Время прибытия автобуса: {flight['Bus_Arrival_Time']:.2f} Час")
        print(f"Точка спроса {flight['Demand_ID']} с сайта {flight['Station_ID']} Взлетайте, взлетайте, время: {flight['Flight_Start_Time']:.2f} часы, время возврата: {flight['Flight_End_Time']:.2f} Почасовая оплата: {flight['Cost']:.2f} юань")
        print("-----")
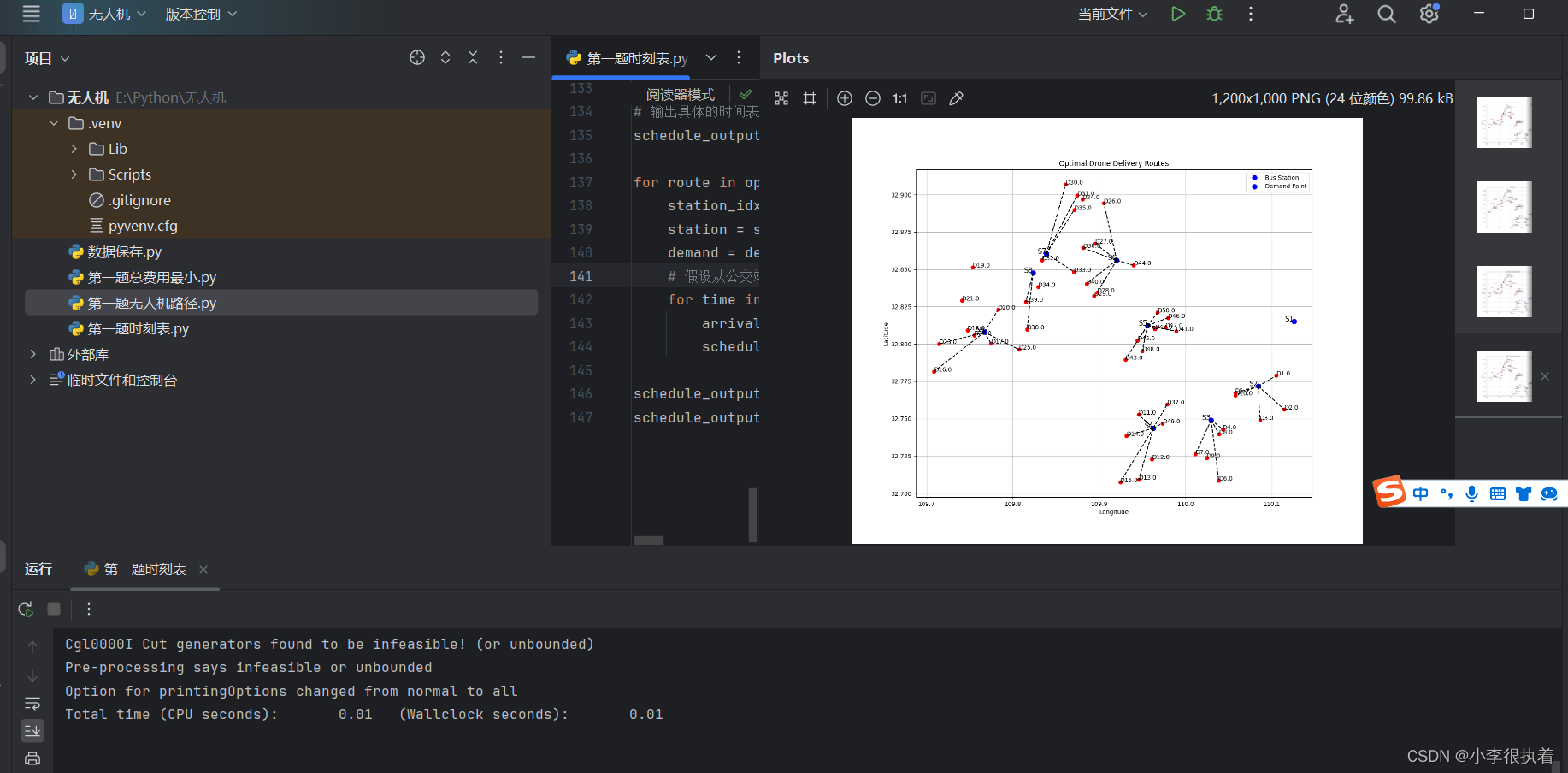
        visited_demands.add(flight['Demand_ID'])
2. Визуализация маршрутов и расписаний полетов

Мы используем Matplotlib для построения траекторий и расписаний полетов.

Язык кода:javascript
копировать
# Визуализируйте траекторию полета
plt.figure(figsize=(10, 8))

# Нарисуйте автобусные остановки
for i, station in stations_data.iterrows():
    plt.plot(station['Longitude'], station['Latitude'], 'bo', markersize=8)
    plt.text(station['Longitude'], station['Latitude'], f'S{i+1}', fontsize=12, ha='right')

# Нарисуйте точки спроса
for j, demand in demands_data.iterrows():
    plt.plot(demand['Longitude'], demand['Latitude'], 'ro', markersize=6)
    plt.text(demand['Longitude'], demand['Latitude'], f'D{demand["Demand_ID"]}', fontsize=10, ha='left')

# Нарисуйте оптимальный путь
for route in optimal_routes:
    station_idx, demand_idx, dist = route
    station = stations_data.iloc[station_idx]
    demand = demands_data.iloc[demand_idx]
    plt.plot([station['Longitude'], demand['Longitude']], [station['Latitude'], demand['Latitude']], 'k--')

plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('Optimal Drone Delivery Routes')
plt.legend(['Bus Station', 'Demand Point'])
plt.grid()
plt.show()

# Вывод конкретного расписания
schedule_output = []

for route in optimal_routes:
    station_idx, demand_idx, dist = route
    station = stations_data.iloc[station_idx]
    demand = demands_data.iloc[demand_idx]
    # Предположим, что время отправления с автовокзала совпадает со временем прибытия автобуса.
    for time in bus_schedule['Байхэ — Цаншан']:
        arrival_time = time + dist / bus_speed
        schedule_output.append((f'Station {station_idx+1}', f'Demand {demand_idx+1}', time, arrival_time))

schedule_output_df = pd.DataFrame(schedule_output, columns=['Station', 'Demand', 'Departure Time', 'Arrival Time'])
schedule_output_df

окончательный результат

boy illustration
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет
boy illustration
Код js веб-страницы, фон частицы, код спецэффектов
boy illustration
【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
boy illustration
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
boy illustration
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!
boy illustration
Как реализовать переход по странице в HTML (html переходит на указанную страницу)
boy illustration
Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?
boy illustration
Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа
boy illustration
Серия uni-app: uni.navigateЧтобы передать скачок значения
boy illustration
Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.
boy illustration
JS-время конвертации
boy illustration
Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены
boy illustration
Поле комментария, щелчок мышью, специальные эффекты, js-код
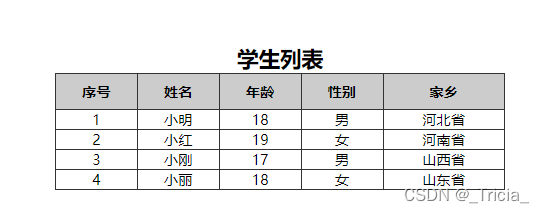
boy illustration
Объект массива перемещения объекта JS
boy illustration
Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
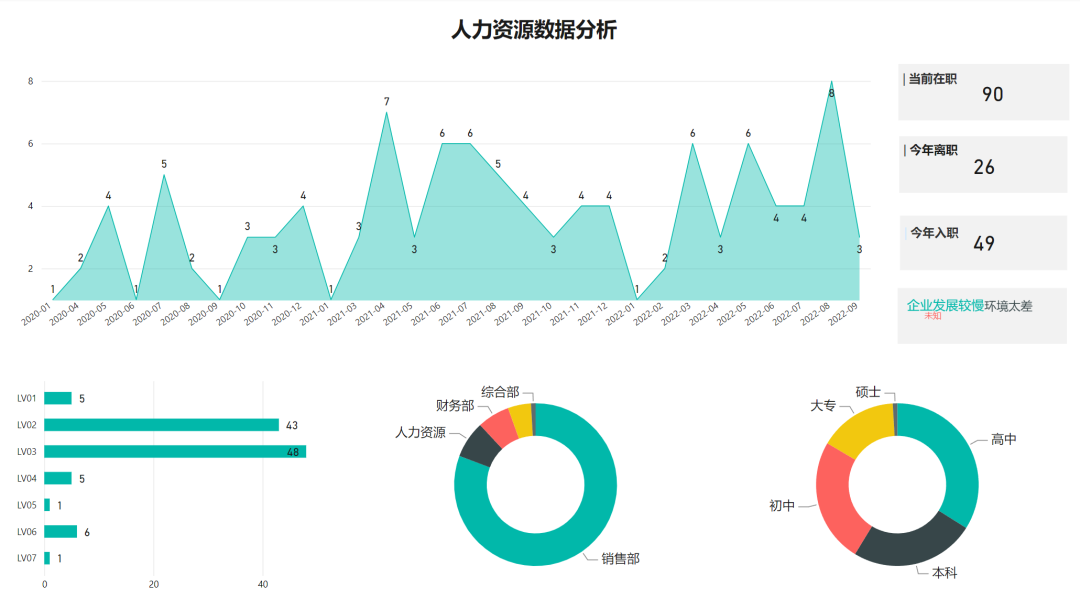
boy illustration
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!
boy illustration
Получить текущее время в js_Как динамически отображать дату и время в js
boy illustration
Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.
boy illustration
У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
boy illustration
Copilot облачной разработки — упрощение разработки
boy illustration
Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов
boy illustration
CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
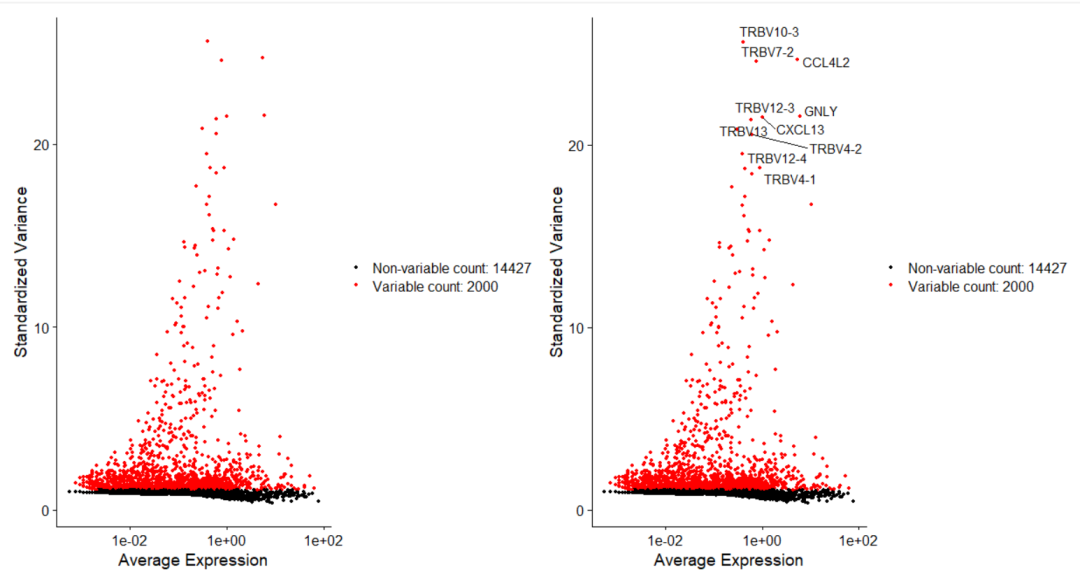
boy illustration
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация
boy illustration
vLLM: мощный инструмент для ускорения вывода ИИ
boy illustration
CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.
boy illustration
Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
boy illustration
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
boy illustration
LM Studio для создания локальных больших моделей
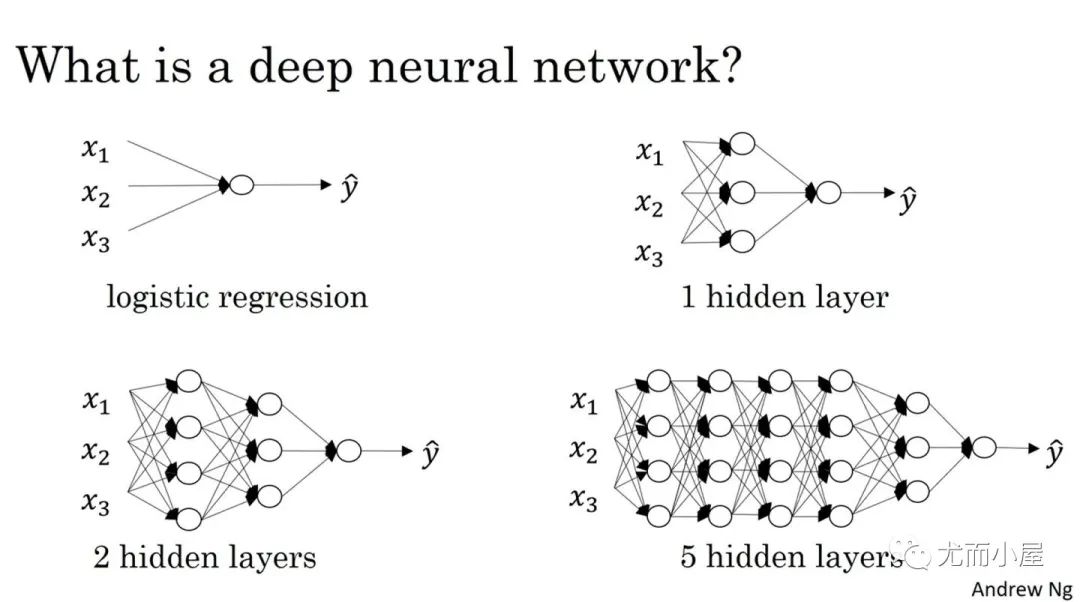
boy illustration
Как определить количество слоев и нейронов скрытых слоев нейронной сети?
boy illustration
[Отслеживание целей] Подробное объяснение ByteTrack и детали кода
©