[Машинное обучение | Серия «Проверка гипотез»] Серия «Проверка гипотез» — тест хи-квадрат (подробные случаи, вывод принципов математических формул). Вы уверены, что хотите взглянуть на наиболее часто игнорируемые проверки гипотез?

🤵♂️ Персональная домашняя страница: @AI_magician 📡Адрес домашней страницы: Об авторе: CSDN-контент-партнер, качественный создатель в сфере full-stack. 👨💻Видение: стремление расти вместе с большим количеством партнеров, которые любят компьютеры! ! 🐱🏍
[Машинное обучение | Серия «Проверка гипотез»] Серия «Проверка гипотез» — тест хи-квадрат (подробные случаи, вывод принципов математических формул). Вы уверены, что хотите взглянуть на наиболее часто игнорируемые проверки гипотез? автор: компьютерный волшебник Версия: 1.0 ( 2023.8.27 )
краткое содержание: Целью этой серии является популяризация основных концепций, которые необходимо передать на пути к глубокому обучению. обучение | Серия «Проверка гипотез»] Серия «Проверка гипотез» — тест хи-квадрат (подробные случаи, вывод принципов математических формул). Вы уверены, что хотите взглянуть на наиболее часто игнорируемые проверки гипотез?
Проверка гипотез
Проверка гипотез — распространенный метод узкого анализа данных.,Используется для проверки гипотез о параметрах популяции.。это может помочь намОпределите, существует ли значительная разница между данными выборки и гипотезой.。Проверка гипотезы обычно включает в себя следующее:шаг:
- Установите нулевую гипотезу (Null Гипотеза) и альтернативная гипотеза (Alternative Гипотеза): Нулевая гипотеза — это определенная гипотеза об общих параметрах, а альтернативная гипотеза — это гипотеза, противоположная нулевой гипотезе.
- Выберите подходящий метод проверки гипотезы. В зависимости от типа исследовательского вопроса выберите подходящий метод проверки гипотезы, например t-тест, тест. хи-квадрат、ANOVAждать。
- Рассчитайте количество тестов: в соответствии с выбранным методом проверки гипотезы рассчитайте соответствующее количество тестов.
- Определите уровень значимости. Установите уровень значимости (например, 0,05), который представляет собой порог отклонения нулевой гипотезы. p значение (p-значение) — индекс вероятности, используемый для измерения результатов статистической проверки гипотез (можно понимать как индекс, используемый для измерения степени противоречия между наблюдаемыми данными и нулевой гипотезой). Он представляет собой вероятность того, что наблюдаемые данные или, в более крайнем случае, возникнут, если нулевая гипотеза (нулевая гипотеза) верна.
- Перейдите к проверке гипотезы ХОРОШО: на основе статистики теста и уровня значимости определите, имеет ли образец данных достаточно доказательств, чтобы поддержать или отвергнуть нулевую гипотезу.
- Сделать выводы: По результатам проверки гипотез сделать выводы об общих параметрах и объяснить их.
Проверка гипотез может помочь нам проверить гипотезы о параметрах популяции, тем самым обеспечивая надежные выводы и заключения в ходе анализа данных. Следовательно, его можно рассматривать как часть анализа данных в узком смысле.
имя | представлять | Преимущества и недостатки |
|---|---|---|
Тест на нормальность | Тест на нормальность используется для определения того, соответствуют ли данные нормальному распределению. Обычно используемые методы проверки нормальности включают тест Колмогорова-Смирнова, тест Шапиро-Уилка и тест Андерсона-Дарлинга. | Преимущества: может помочь определить, подходят ли данные для использования статистических методов, основанных на нормальном распределении. Недостатки: при больших выборках данных даже небольшие отклонения могут привести к отклонению предположения о нормальности. |
Корреляционный тест | Корреляционные тесты используются для определения корреляции между двумя переменными. Обычно используемые методы корреляционного теста включают коэффициент корреляции Пирсона, коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла. (Этот алгоритм тестирования можно использовать только для числовых типов, а не для категориальных типов) | Преимущества: Может измерять линейные или нелинейные зависимости между переменными. Недостатки: Корреляция не указывает на причинно-следственную связь, а лишь указывает на степень связи между переменными. |
Обнаружение выбросов | Обнаружение выбросов используется для выявления точек данных с необычными характеристиками в наборе данных. Обычно используемые методы обнаружения выбросов включают метод статистического Z-показателя, принцип 3σ, метод коробчатой диаграммы и методы, основанные на расстоянии (например, DBSCAN). | Преимущества: он может помочь выявить выбросы и полезен для очистки данных и обработки ненормальных данных. Недостатки: Некоторые методы сложнее обрабатывать многомерные и многомерные данные. |
Дисперсионный анализ (ANOVA) | Дисперсионный анализ используется для сравнения того, существенно ли различаются средние значения двух или более групп. Обычно используемые методы дисперсионного анализа включают однофакторный дисперсионный анализ и многофакторный дисперсионный анализ. | Преимущества: Подходит для сравнения различий между несколькими группами, обеспечивая эффективный статистический вывод. Недостатки: может быть неприменим к данным с ненормальным распределением и небольшим размерам выборки. |
t-тест | T-критерий используется для сравнения того, существует ли значительная разница в средних значениях между двумя группами. Обычно используемые методы t-критерия включают t-критерий независимой выборки и t-критерий парной выборки. | Преимущества: Простой и удобный в использовании, подходит для небольших выборок данных. Недостатки: могут быть неточными для данных с ненормальным распределением и чувствительны к выбросам. |
Тест хи-квадрат (Chi-Square Test) | Тест хи-квадрат используется для сравнения корреляции между двумя или более категориями переменная. Часто используемый Тест Метод хи-квадрата включает в себя тест независимости хи-квадрат и критерий согласия хи-квадрат. | Преимущества: Подходит для статистического вывода категориальных данных, используемых для проверки разницы между наблюдаемыми частотами и ожидаемыми частотами. Недостатки: Может быть неточным для небольших размеров выборки или низких ожидаемых частот. |
Тест на стационарность | Статистический метод тестирования, используемый для проверки того, являются ли данные временных рядов стационарными. Стационарность означает, что статистические свойства временного ряда остаются неизменными в разные периоды времени. | Преимущества: он может определить, являются ли данные временных рядов стационарными, и обеспечить основу для последующего анализа временных рядов. Недостатки: разные методы тестирования на стационарность могут давать разные результаты, поэтому необходимо комплексно рассматривать несколько методов тестирования. |
Тест на белый шум | Статистический метод тестирования, используемый для проверки того, соответствуют ли данные временных рядов процессу белого шума. Белый шум относится к последовательности случайных величин, которые независимы друг от друга и имеют нулевое среднее, и между последовательностями нет корреляции. | Преимущества: он может проверить, являются ли данные временных рядов случайными и независимыми, что важно для рациональности анализа временных рядов. Недостатки: разные методы проверки белого шума могут давать разные результаты, поэтому необходимо комплексно рассматривать несколько методов проверки. |
Тест хи-квадрат
Тест хи-квадрат(Chi-square тест) определяется распределением хи-квадрат (хи-квадрат Статистический метод, основанный на распределении. Распределение хи-квадрат было первоначально разработано британским статистиком Карлом Пирсоном. Пирсоном в 1900 году, он обеспечивает эффективный метод анализа и объяснения корреляции дискретных типов, помогая исследователям делать выводы и выводы. Тест хи-квадрат разработан на основе концепции распределения хи-квадрат.,С тех пор он широко используется в областях применения статистики.,Например, медицинские исследования, социологические опрос、Исследование рынка и т. д.
Расчет статистики хи-квадрат основан на разнице между наблюдаемой частотой и ожидаемой частотой. Чем больше разница, тем больше значение статистики хи-квадрат. Распределение статистики хи-квадрат связано со степенями свободы. Вы можете использовать таблицу распределения хи-квадрат или статистическое программное обеспечение, чтобы определить соответствующий уровень значимости. Обычно мы выбираем уровень значимости (например, 0,05). Если рассчитанная статистика хи-квадрат превышает критическое значение соответствующих степеней свободы и уровня значимости, мы отвергаем нулевую гипотезу и считаем, что наблюдаемая частота равна. с ожидаемой частотой. Между переменными существует значительная разница, то есть существует связь или независимость между переменными отвергается.
Предположим, у нас есть двумерная таблица сопряженности, содержащая наблюдаемые частоты двух категориальных переменных. Таблица выглядит следующим образом:
ПеременнаяB=0 | ПеременнаяB=1 | общий | |
|---|---|---|---|
Сумма изменения A=0 | a | b | a+b |
Сумма сдачи A=1 | c | d | c+d |
общий | a+c | b+d | a+b+c+d |
Среди них a, b, c и d представляют частоты наблюдений в четырех сетках соответственно.
Тест Нулевая гипотеза хи-квадрата (нулевая Гипотеза) такова: переменная А и переменная В независимы друг от друга, то есть между ними нет значимой корреляции. альтернативная гипотеза Гипотеза) такова: переменная А и переменная Б связаны, то есть между ними существует значительная корреляция.
Тест хи-квадратизшагследующее:
Шаг 1. Рассчитайте ожидаемую частоту
Во-первых, нам нужно вычислить ожидаемую частоту каждой ячейки, то есть ожидаемую частоту в каждой ячейке, предполагая, что переменная A и переменная B независимы. Формула расчета ожидаемой частоты выглядит следующим образом:
Тест хи-квадрат中из期望频числодаПо нулевой гипотезе (переменнаяAипеременнаяB независима)(это важно!!)来计算из。预期频числоиз计算采用了边际总频числои ХОРОШО、列边际频числоиз乘积。 Если предположить, что переменная A и переменная B независимы, то между значением переменной A (0 или 1) и значением переменной B (0 или 1) не должно быть корреляции. Следовательно, мы можем применить соответствующую пропорцию в популяции к предельной частоте в каждой ячейке. Учитывая предельные частоты в каждой ячейке, мы можем вычислить ожидаемые частоты
, где i представляет индекс строки, а j представляет индекс столбца:
Вывод этой формулы расчета следующий:
- первый,Мы рассматриваем случай, когда значение переменнойA равно 0. в этом случае,Сумма изменения Вероятность A=0 равна
(a+b да Сумма изменения Предельная частота A=0, a+b+c+d — общая предельная частота). Аналогично вероятность того, что ПеременнаяB=0 равна
. Поскольку мы предполагаем, что переменнаяAипеременнаяB независима, мы можем перемножить эти две вероятности, чтобы получить совместную вероятность суммы изменений A=0 и ПеременнаяB=0:
。
- Затем мы умножаем совместную вероятность на предельную частоту совокупности.
, чтобы получить ожидаемую частоту сумм изменений A=0 и ПеременнаяB=0
. Следовательно, получаем числительную часть формулы:
. Аналогичным образом мы можем получить ожидаемые частоты для других сеток.
Таким образом, мы получаем Тест Формула расчета ожидаемой частоты в хи-квадрате. Следует отметить, что ожидаемая частота рассчитывается по нулевой гипотезе, предполагая, что переменная A и переменная B независимы. Если существует значительная разница между наблюдаемой частотой и ожидаемой частотой, то мы отвергнем нулевую гипотезу и сочтем, что существует значительная связь между переменной A и переменной B.
в,
Представляет ожидаемую частоту ячейки в строке i и столбце j. (здесь я = 1, j = 1)
Шаг 2. Рассчитайте статистику хи-квадрат.
Затем мы вычисляем статистику хи-квадрат, которая измеряет разницу между наблюдаемыми и ожидаемыми частотами. Формула расчета статистики хи-квадрат выглядит следующим образом:
в,
представляет статистику хи-квадрат,
Представляет частоту наблюдения ячейки в i-й строке и j-м столбце,
Представляет ожидаемую частоту ячейки в строке i и столбце j.
Шаг 3: Рассчитайте степени свободы
Степени свободы — это количество наблюдений в величине хи-квадрат, которое может свободно изменяться. в Тест В хи-квадрате формула расчета степеней свободы выглядит следующим образом (найти соответствующее критическое значение или рассчитать по таблице распределения хи-квадрат p ценить):
Формула степеней свободы основана на Тесте. Определяется размерами двумерной таблицы сопряженности в хи-квадрате.。В двумерной таблице непредвиденных обстоятельств,ХОРОШОи列изчисло量分别为 r и c。 Предположим, у нас есть r ХОРОШО c Двумерная таблица сопряженности столбцов. Расчет степеней свободы основан на следующих принципах:
- В направлении ХОРОШО,Мы вольны выбирать частоту наблюдений для каждой ячейки,Но оно должно удовлетворять предельной частоте ХОРОШО.
- В направлении столбца мы также можем свободно выбирать частоту наблюдения каждой ячейки, но также должна соблюдаться граничная частота столбца.
Следовательно, для каждой ячейки у нас есть одна степень свободы. Сумма степеней свободы равна сумме степеней свободы всех ячеек. В двумерной таблице сопряженности известны граничные частоты столбцов ХОРОШОи, поэтому нам нужно только определить наблюдаемую частоту для каждой ячейки. Как только мы выберем r ХОРОШО c Если указана частота наблюдения ячейки, частота наблюдения других ячеек будет фиксированной. Чтобы поддерживать постоянные предельные частоты,нам нужна базаОграничения по предельной частоте для выбора частот наблюдения。Для двумерной таблицы сопряженности,Есть два ограничения,Один из них — предельная частота ХОРОШО.,另一индивидуальныйда列边际频число。 Принимая во внимание эти ограничения, количество ячеек, которые мы можем свободно выбирать, равно (r-1) × (c-1)。这да因为,Как только мы выберем частоту наблюдения одной из ячеек,Частоты наблюдения других ячеек в столбце ХОРОШО будут зафиксированы в соответствии с ограничениями.
в,
выражать ХОРОШОчисло,
Представляет количество столбцов.
Шаг 4: Рассчитайте значение p
Мы рассчитываем на основе статистики хи-квадрат количества и степеней свободы. p Распространенный метод - сравнить величину статистики хи-квадрат с распределением хи-квадрат, соответствующим степеням свободы, и вычислить вероятность попадания в более крайнюю область. Это можно рассчитать, просмотрев таблицу распределения хи-квадрат или используя статистическое программное обеспечение. В практических приложениях для расчета обычно используются пакеты программного обеспечения (такие как библиотека Python SciPy или пакет статистики на языке R). p ценить.
По заданному уровню значимости (значимость уровень), обычно выбирают p Значение сравнивается с уровнем значимости. если p Значение меньше уровня значимости, обычно 0,05, мы можем отвергнуть нулевую гипотезу и подумать, что между переменной A и переменной B существует значимая связь, в противном случае мы принимаем нулевую гипотезу и думаем, что между переменной нет значимой связи; А и переменная Б.
Ниже приведен реальный и простой случай, иллюстрирующий Тест. хи-квадратиз流程ипринцип:
Предположим, мы хотим учитьсямужскойиженщина之间да否存在喜欢不同类型电影из差异。Мы случайно выбрали100индивидуальныймужскойи100индивидуальныйженщина,并记录了他们对三种类型电影из喜好(Категория А、Категория Би Категория С)。
Наблюдаемые частоты следующие:
Категория А Категория Б Категория С
мужской 30 35 35
женщина 45 25 30первый,Нам нужно выдвинуть гипотезы. здесь,我们из原гипотезада“мужскойиженщина对不同类型电影из喜好没有差异”。备择гипотезада“мужскойиженщина对不同类型电影из喜好有差异”。
Следующий,Рассчитаем ожидаемую частоту. Ожидаемая частота основана на нулевой гипотезе.,гипотезамужскойиженщина对电影类型из喜好да独立из。我们可以通过公式计算期望频числоследующее:
Категория А Категория Б Категория С
мужской 37.5 32.5 30
женщина 37.5 32.5 30Затем мы вычисляем статистику хи-квадрат. Статистика хи-квадрат измеряет разницу между наблюдаемой частотой и ожидаемой частотой. Мы можем рассчитать статистику хи-квадрат как:
Сумма статистики хи-квадрат = [(30-37,5)²/37,5] + [(35-32,5)²/32,5] + [(35-30)²/30] + [(45-37,5)²/37,5] + [ (25-32,5)²/32,5] + [(30-30)²/30] ≈ 6,8Наконец, нам нужно определить уровень значимости статистики хи-квадрат. Мы используем степени свободы для определения уровня значимости, в данном случае (2-1) × (3-1) = 2.
Мы можем использовать таблицу распределения хи-квадрат или статистическое программное обеспечение, чтобы найти соответствующий уровень значимости для статистики хи-квадрат. Предполагая, что мы используем уровень значимости 0,05 и 2 степени свободы, мы обнаруживаем, что критическое значение статистики хи-квадрат составляет 5,99. Начиная с версии 6.8 > 5.99,Мы можем отвергнуть нулевую гипотезу,Примите альтернативную гипотезу,Прямо сейчасмужскойиженщина对不同类型电影из喜好存在差异。
Критическое значение — это граница, при которой нулевая гипотеза отвергается на уровне значимости. Если наблюдаемая статистика хи-квадрат превышает критическое значение, мы можем отвергнуть нулевую гипотезу.


Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
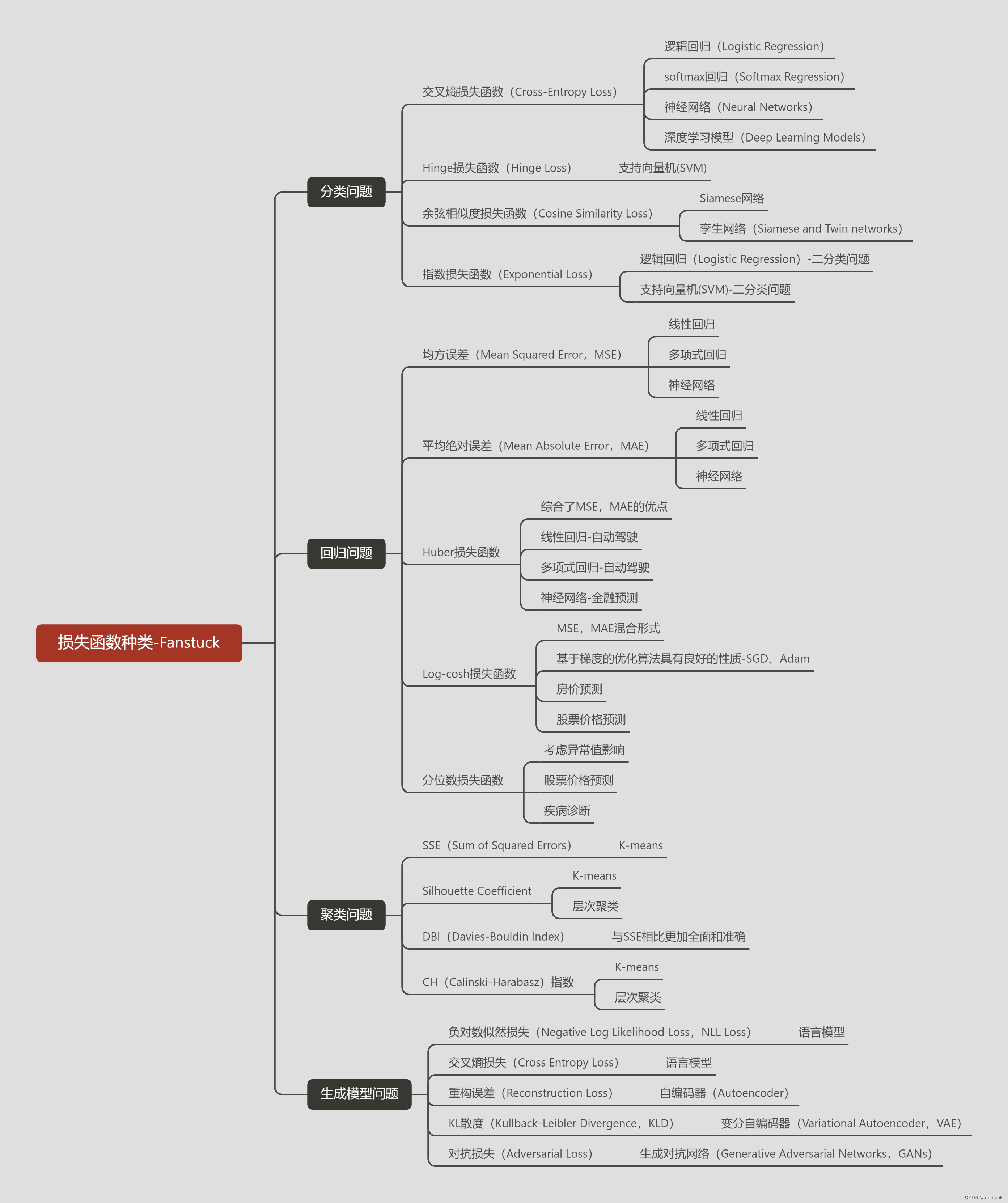
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
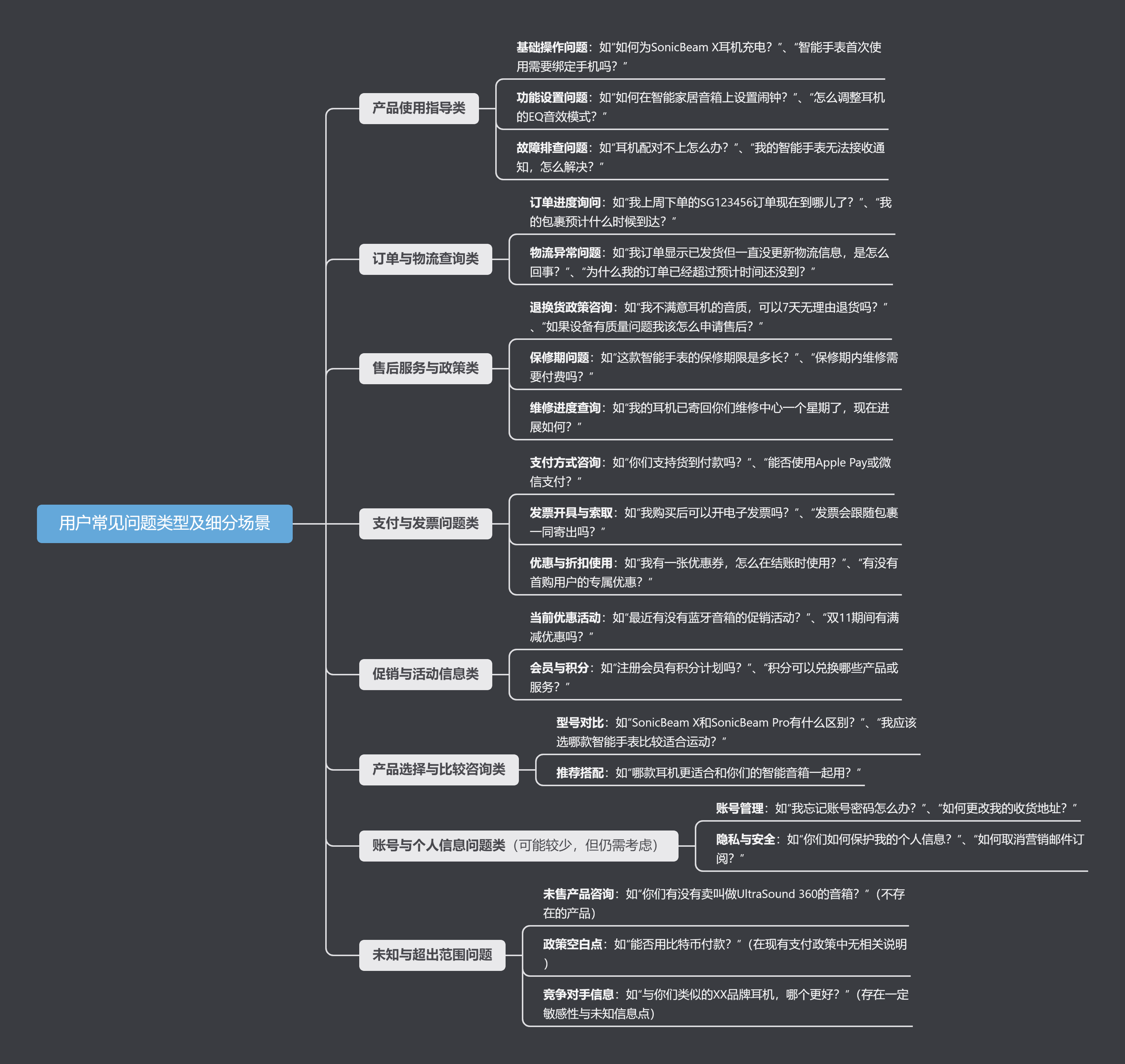
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
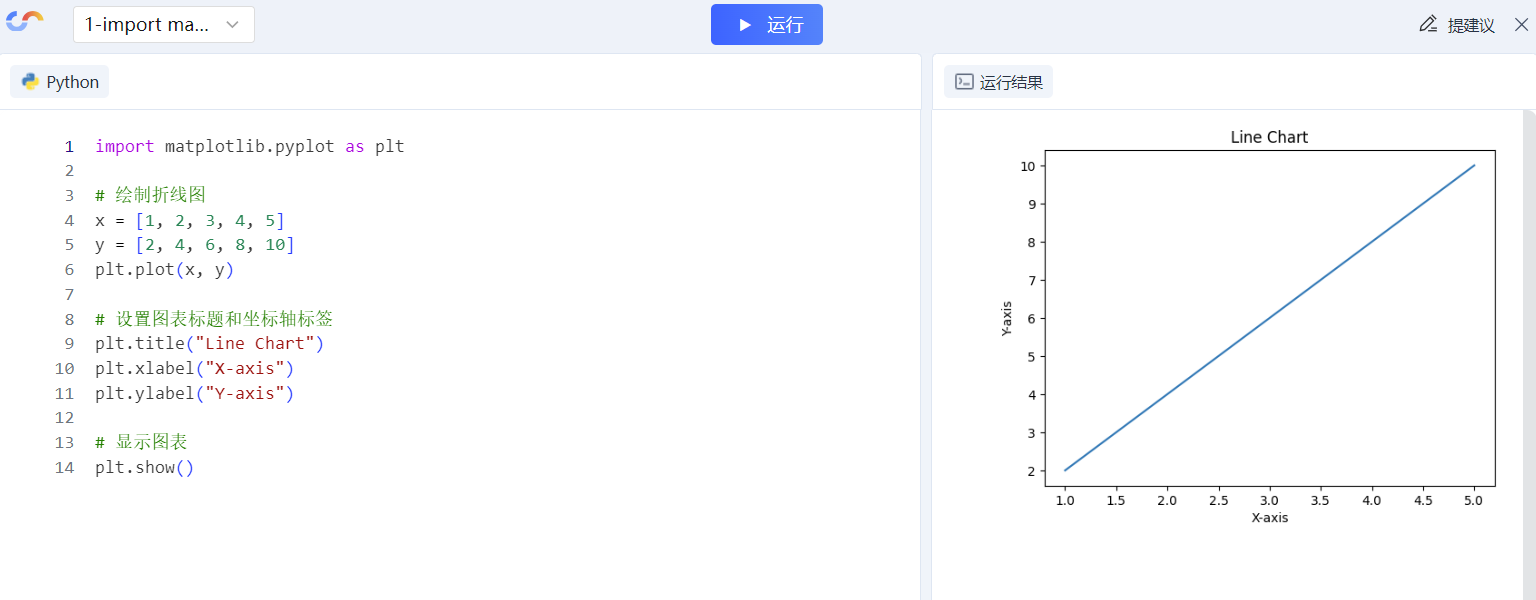
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
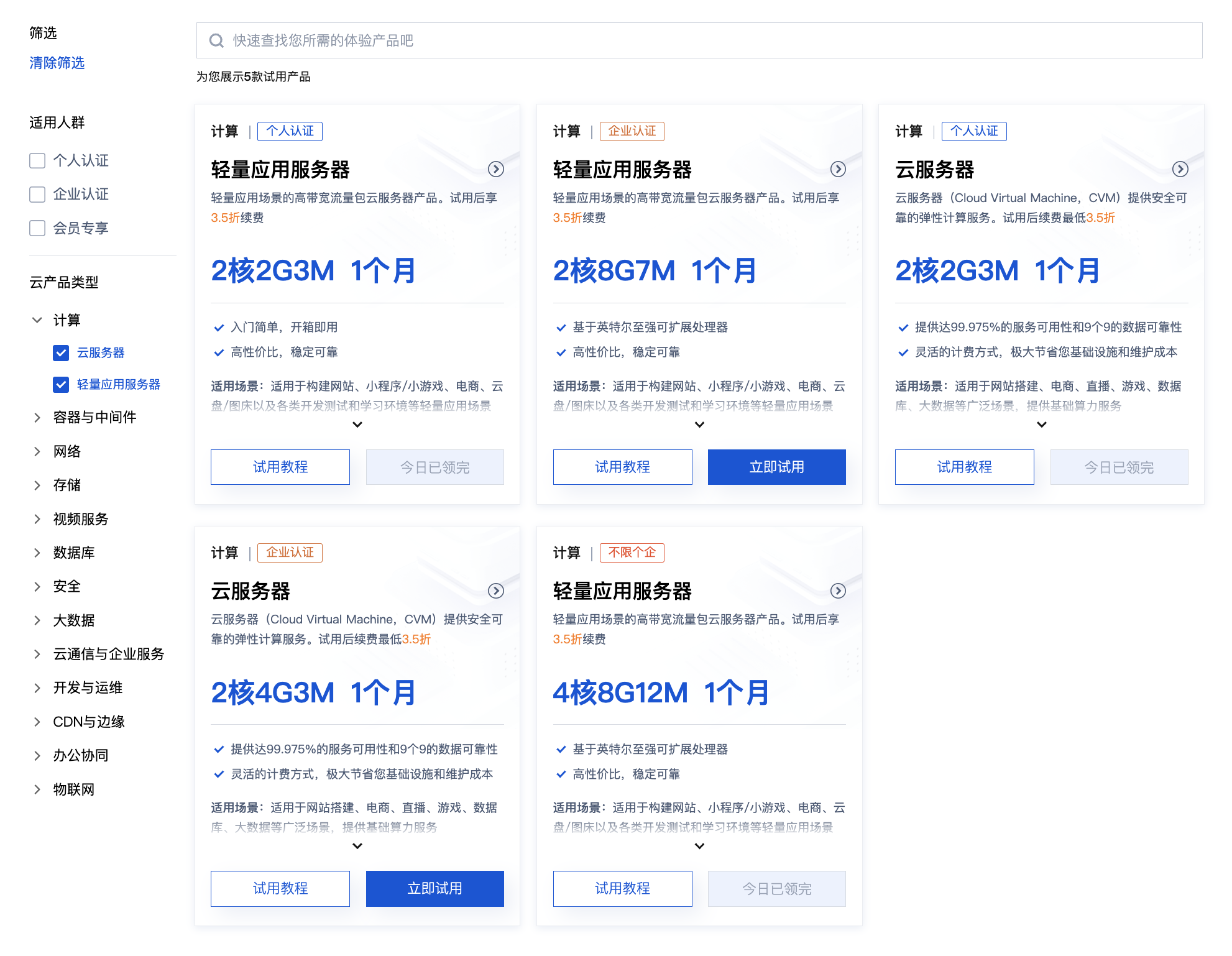
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.