1. Введение концепции

1. Функция потери

Функция потерь относится к функции, которая сопоставляет событие (элемент в пространстве выборки) с действительным числом, которое выражает экономические затраты или альтернативные издержки, связанные с этим событием. В машинном обучении функция потерь часто связана с задачами оптимизации как критерий обучения, то есть решение и оценка модели путем минимизации функции потерь. Для разных типов задач требуются разные функции потерь. Например, среднеквадратическая ошибка обычно используется в качестве функции потерь в задачах регрессии, а перекрестная энтропия обычно используется в качестве функции потерь в задачах классификации.

2. Среднеквадратическая функция потерь разности

Определение следующее:

L(y,f(x;\Theta )) = \frac{1}{N}\sum_{i = 1}^{N}(yi - f(xi;\Theta ))^{2}

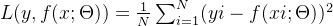
Значение: N — количество выборок. Формула выражается как среднее квадратов каждого истинного значения, вычтенного из прогнозируемого значения. Чем меньше значение среднеквадратического отклонения, тем лучше модель. Для проблем регрессии,Производная функции потерь среднеквадратической ошибки локально монотонна.,Оптимальное решение можно найти. Но для задач классификации,Функция потерь может быть питтинговой,Трудно найти оптимальное решение。Следовательно, функция потерь среднеквадратической ошибки подходит для задач регрессии.。

3. Функция перекрестной энтропийной потери

Перекрестная энтропия — важное понятие в теории информации, которое в основном используется для измерения разницы между двумя распределениями вероятностей. В машинном обучении перекрестная энтропия представляет собой разницу между истинным распределением вероятностей и прогнозируемым распределением вероятностей. Чем меньше значение, тем лучше эффект прогнозирования модели. Формула функции перекрестных потерь энтропии:

L = -(y log \hat{y} +(1-y)log(1- \hat{y}))

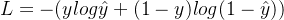
Среди них y представляет истинную метку выборки, а \hat{y} представляет метку, предсказанную моделью. Когда y=1, это означает, что образец принадлежит положительному классу; когда y=0, это означает, что образец принадлежит отрицательному классу;

3.1 Количество информации

Информационное содержание — это мера того, сколько информации имеется. Например

• 1: Солнце встает с востока, количество информации 0, потому что это ерунда. Не существует такой вещи, как неопределенность.
• 2: Сегодня будет дождь. Интуитивно,Этот объем информации относительно велик.,Потому что сегодняшняя погода неопределенна,Но это предложение устраняет неопределённость.

На основании вышеизложенного итог таков: количество информации обратно пропорционально вероятности появления информации. Чем больше вероятность, тем меньше количество информации, и чем меньше вероятность, тем больше количество информации. Предположим, что вероятность того, что что-то произойдет, равна p(xi), тогда количество информации равно:

I(xj) = -ln(p(xi))

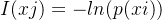
3.2 Информационная энтропия

Информационная энтропия — важное понятие в теории информации, используемое для измерения неопределенности или случайности количества информации в системе или сигнале. Определение информационной энтропии можно выразить математической формулой. Предположим, существует дискретная случайная величина X, которая может принимать n различных возможных значений.

x_1,x_2,\ldots,x_n

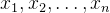
, вероятность каждого возможного значения равна

p_1,p_2,\ldots,p_n

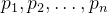
, то формула расчета информационной энтропии H(X) имеет вид:

H(X)=-\sum_{i=1}^{n}p_i\log_2p_i

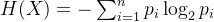
в,

\log_2

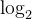
Представляет логарифм по основанию 2. Физический смысл информационной энтропии таков: она представляет собой среднюю неопределенность или объем информации системы с учетом распределения вероятностей. Чем больше значение информационной энтропии, тем выше неопределенность системы; чем меньше значение информационной энтропии, тем ниже неопределенность системы.

3.3 Относительная энтропия

относительная энтропия,также известный какKL Дивергенция (Кульбак-Лейблер Divergence）,Это мера, используемая для сравнения разницы между двумя распределениями вероятностей. Он измеряет степень различия между одним распределением вероятностей P и другим эталонным распределением вероятностей Q. Относительная энтропия как определяется:

D_{KL}(P||Q)=\sum_{x}P(x)\log\frac{P(x)}{Q(x)}

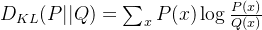
в,P(x)иQ(x) — вероятности распределения вероятностей PиQ по событию x соответственно. Физический смысл относительной энтропии таков: она представляет собой количество дополнительной информации, необходимой для представления распределения вероятностей P как кодирования эталонного распределения вероятностей Q. Если P и Q очень близки, значение относительной энтропии будет относительно небольшим, если P и Q сильно различаются, значение относительной энтропии будет относительно большим. Дивергенция КЛ = перекрестная энтропия - информационная энтропия Относительная энтропия имеет широкое применение в машинном обучении, теории информации и статистике. Его можно использовать для оценки сходства двух моделей или распределений вероятностей, сравнения различий в распределениях данных, выполнения оптимизации в рамках минимизации энтропии и т. д. Например, в машинном обучении относительная энтропия часто используется для сравнения разницы между распределением реальных данных и распределением, предсказанным моделью, чтобы оценить производительность модели. Меньшее значение относительной энтропии указывает на то, что предсказанное моделью распределение ближе к истинному распределению.

2. Перекрестная энтропия в задачах классификации

1. Перекрестная энтропия в задаче бинарной классификации

Разложим формулу перекрестной энтропии двух категорий (4) на две ситуации:

• когда y=1 когда , то есть значение метки равно 1 ,это Положительный например, элемент после знака плюс:

loss=-log(a)

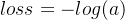
• когда y=0 когда , то есть значение метки равно 0 , является Контрпримером, элемент перед знаком плюса равен 0 :

loss=-log(1-a)

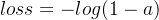
По оси абсцисс — прогнозируемый результат, а по оси ординат — значение функции потерь. y=1 означает, что текущее значение метки выборки равно 1. Когда прогнозируемый результат ближе к 1, значение функции потерь меньше и результаты обучения становятся более точными. Когда прогнозируемый результат ближе к 0, значение функции потерь больше и результаты обучения хуже. В настоящее время значение функции потерь показано на рисунке ниже.

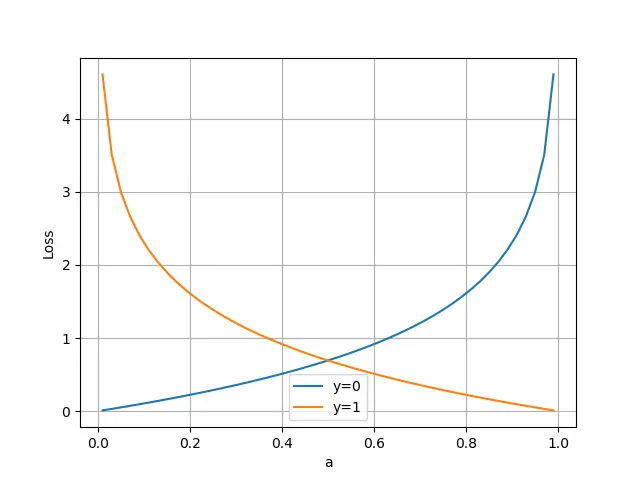
2. Перекрестная энтропия в задачах мультиклассификации

Предположим, вы хотите предсказать категорию животного на основе его контура, цвета и других особенностей на изображении. Есть три предсказуемые категории: кошки, собаки и свиньи. Предположим, мы обучаем две модели классификации, и результаты их прогнозирования следующие: Модель1: Верно ли прогнозируемое значение метки значения 0,3? 0.3 0.40 0 1 (Свинья) Правильно 0,3 0.4 0.40 1 0 (собака) правильно 0,1 0.2 0.71 0 0 (кот) ошибок Каждая строка представляет прогноз различных выборок, общедоступных 3 образцы. Видно, что модель 1 для образца 1 и образцы 2 Правильный с очень небольшим отрывом, для образца 3 Решение совершенно неверное. Модель2: Верно ли прогнозируемое значение метки значения 0,1? 0.2 0.70 0 1 (свинья) правильно 0,1 0.7 0.20 1 0 (собака) правильно 0,3 0.4 0.41 0 0 (кот) ошибок Видно, что модель 2 для образца 1 и образцы 2 Суждение очень точное (прогнозированное значение вероятности ближе к 1）,для образца 3 Хотя суждение было ошибочным, оно не было слишком уж ошибочным (прогнозированное значение вероятности было намного меньше, чем 1）。 В сочетании с формулой многоклассовой функции перекрестных энтропийных потерь модель может быть получена 1 Перекрестная энтропия равна: sample 1 loss = -(0 * log(0.3) + 0 * log(0.3) + 1 * log(0.4)) = 0.91 sample 1 loss = -(0 * log(0.3) + 1 * log(0.4) + 0 * log(0.4)) = 0.91 sample 1 loss = -(1 * log(0.1) + 0 * log(0.2) + 0 * log(0.7)) = 2.30 для всех образцов loss Найдите среднее значение:

L=\frac{0.91+0.91+2.3}{3}=1.37

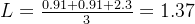
Модель 2 Перекрестная энтропия равна: sample 1 loss = -(0 * log(0.1) + 0 * log(0.2) + 1 * log(0.7)) = 0.35 sample 1 loss = -(0 * log(0.1) + 1 * log(0.7) + 0 * log(0.2)) = 0.35 sample 1 loss = -(1 * log(0.3) + 0 * log(0.4) + 0 * log(0.4)) = 1.20 для всех образцов loss Найдите среднее значение:

L=\frac{0.35+0.35+1.2}{3}=0.63

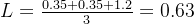
Как видите, 0,63. Сравнивать 1.37 Значение потерь намного меньше, что показывает, что прогнозируемое значение ближе к истинному значению метки, то есть функция перекрестной энтропийной потери может лучше фиксировать Модель 1 и Модель 2 Различия в эффективности прогнозирования。Чем меньше значение функции перекрестных энтропийных потерь, тем меньше интенсивность обратного распространения ошибки.。 Справочная статья-Функция потерь | Функция перекрестных энтропийных потерь。

3. Принцип и процесс вывода функции перекрестных энтропийных потерь.

выражение Когда выходная метка выражена как 10,1}, функция выражения потерь равна:

L = -(y log \hat{y} +(1-y)log(1- \hat{y}))

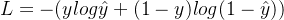
Две категории Две категория вопрос, гипотеза

y\epsilon (0,1)

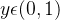
Положительный пример:

P(y = 1 |x) = \hat{y}

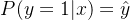
официальный 1 Контрпример:

P(y = 0|x) = 1-\hat{y}

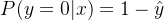
официальный 2 Ляньли Умножьте два приведенных выше уравнения вместе.

P(y | x) = \hat{y}^{y}*(1-\hat{y})^{1-y}

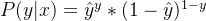
; в

y\epsilon (0,1)

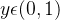
официальный 3 когдаy=1час,официальный 3иофициальный 1 то же самое. когдаy=0час,официальный 3иофициальный 2 то же самое. Возьмите логарифм Возьмите логарифм, удобный для вычислений и не меняющий монотонности функции.

logp(y|x) = ylog\hat{y}+(1-y)log(1-\hat{y})

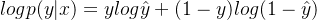
Формула 4 мы надеемся

P(y|x)

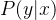
Чем больше, тем лучше, т.е. пусть отрицательные значения

-logP(y|x)

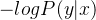
Чем меньше, тем лучше, Функция потерь получается как

L = -(y log \hat{y} +(1-y)log(1- \hat{y}))

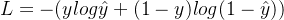
официальный 5 Пополнить Когда все вышеперечисленное относится к одному образцу, выражение нескольких образцов таково: вероятность нескольких образцов - это совместная вероятность, которая равна произведению каждого из них.

p(y |x) = \prod_{i}^{m}p(y^{(i)}|x^{(i)})

logp(y|x)= \sum_{i}^{m}logp(y^{(i)}x^{(i)})

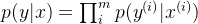
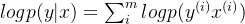
Зависит отофициальный 4иофициальный 5 получил

logp(y^{(i)} |x^{(i)})=-L(y^{(i)}|x^{(i)})

logp(y^{(i)}|x^{(i)})=-\sum_{i}^{m}L(y^{(i)}|x^{(i)})

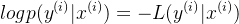
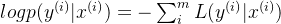
плюс

\frac{1}{m}

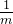
Масштабируйте уравнение. Легко посчитать.

Cost(min):J(w,b) = \frac{1}{m}\sum_{i}^{m}L(y^{(i)}|x^{(i)})

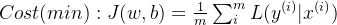
или писать

J=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})]

4. Кодовая реализация функции перекрестной энтропии

На Python,Можно использоватьNumPyбиблиотека илиструктура глубокого обучения（нравитьсяTensorFlow、PyTorch) для расчета функции потери перекрестной энтропии. Ниже приведен расчет числа Две с использованием NumPy. категориии Многоклассовая функция потери перекрестной энтропии Пример кода для：

import numpy as np

# Две Категория Перекрестная потеря энтропиифункция
def binary_cross_entropy_loss(y_true, y_pred):
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

# Многоклассовая функция потери перекрестной энтропии
def categorical_cross_entropy_loss(y_true, y_pred):
    num_classes = y_true.shape[1]
    return -np.mean(np.sum(y_true * np.log(y_pred + 1e-9), axis=1))

# Пример использования
# Две категории
y_true_binary = np.array([[0], [1], [1], [0]])
y_pred_binary = np.array([[0.1], [0.9], [0.8], [0.4]])
loss_binary = binary_cross_entropy_loss(y_true_binary, y_pred_binary)
print("Binary Cross-Entropy Loss:", loss_binary)

# Несколько категорий
y_true_categorical = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
y_pred_categorical = np.array([[0.7, 0.2, 0.1], [0.1, 0.8, 0.1], [0.2, 0.2, 0.6]])
loss_categorical = categorical_cross_entropy_loss(y_true_categorical, y_pred_categorical)
print("Categorical Cross-Entropy Loss:", loss_categorical)

пожалуйста, обрати внимание,Приведенный выше пример кода предназначен только для демонстрационных целей.,В реальных условиях можно использовать структуру глубокого Обучение обеспечивает функцию перекрестной энтропийной потери, поскольку они, как правило, более стабильны в оптимизации. Например, в TensorFlow вы можете использовать класс tf.keras.losses.BinaryCrossentropytf.keras.losses.CategoricalCrossentropy для вычисления Две категориии Многоклассовая функция потери перекрестной энтропии。существоватьPyTorchсередина,Соответствующую функцию потерь можно рассчитать с помощью класса torch.nn.BCELossиtorch.nn.CrossEntropyLoss.

Код взят изhttps://blog.csdn.net/qlkaicx/article/details/136100406

5. Преимущества и недостатки функции перекрестной энтропии.

1. Преимущества

При использовании метода градиентного спуска для обновления параметров скорость обучения Модели зависит от двух величин: 1、скорость обучения； 2、стоимость частной производной; Среди них скорость обучения — это гиперпараметр, который нам нужно установить, поэтому мы ориентируемся на значение частной производной. Из приведенной выше формулы мы находим, что значение частной производной зависит от

и

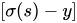
,Наше вниманиесосредоточиться Последнее значение отражает степень ошибки нашей Модели. Чем больше значение, тем хуже эффект Модели. Однако, чем больше значение, тем больше будет значение частной производной, так что Модель обучится. Быстрее. Следовательно, при использовании логической функции для получения вероятности и объединении ее с функцией перекрестной энтропии при потере скорость обучения увеличивается, когда эффект Модели плохой, и скорость обучения становится медленнее, когда эффект Модели хороший.

2. Недостатки

Дэн предложил ArcFace Loss в 2019 году и упомянул в статье два недостатка Softmax Loss:

• 1. С увеличением количества классификаций увеличиваются и параметры матрицы линейного изменения слоя классификации;
• 2. Для задач классификации закрытого набора изученные признаки можно разделить, но для задач распознавания лиц с открытым набором изученные признаки недостаточно различимы. Что касается задачи распознавания лиц, то, во-первых, существует много лиц (соответствует количеству категорий), и новые лица будут продолжать поступать, поэтому это не проблема классификации закрытого множества.

Кроме того, сигмоид(softmax)+перекрестная энтропия потеря хороша для усвоения информации между занятиями.,Потому что он использует механизм межклассовой конкуренции.,Его заботит только точность прогнозирования вероятности правильной метки.,Различия в других неправильных метках игнорируются.,В результате изученные функции разбросаны. Существует множество оптимизаций, основанных на этом вопросе.,Сравнивать, например, улучшать softmax,Такие как L-Softmax, SM-Softmax, AM-Softmax и т. д.