1. Краткое описание концепции

        линейная регрессияпереданоОдна или несколько независимых и зависимых переменныхРегрессионный анализ для моделирования между,Он характеризуется линейной комбинацией одного или нескольких параметров модели, называемых коэффициентами регрессии. Как показано ниже,Точки выборки представляют собой исторические данные.,Кривая регрессии должна наиболее точно имитировать тенденцию точек выборки и минимизировать ошибку.。

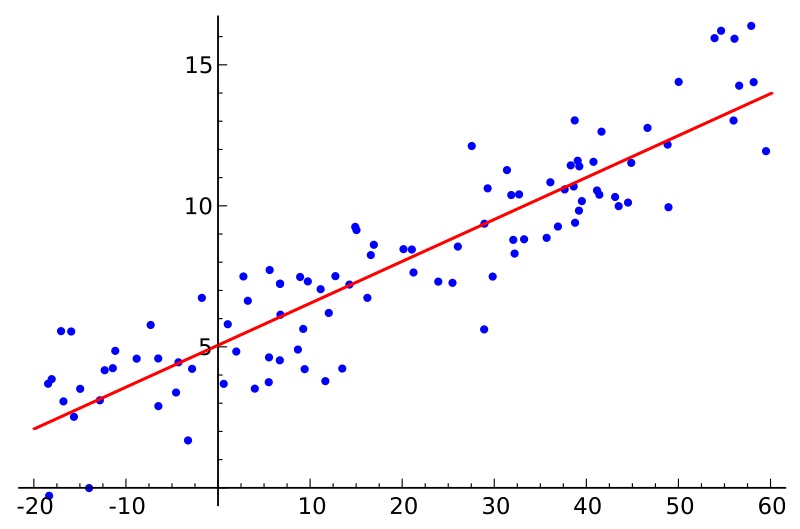
2. Уравнение линейной регрессии

        Уравнение линейной регрессии: n функции, а затем каждая функция Xi Имеются соответствующие коэффициенты Wi , а в случае, когда все собственные значения равны 0, целевое значение имеет значение по умолчанию W0 ,поэтому:

уравнение линейной регрессиидля：

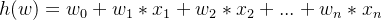
Интегрированная формула:

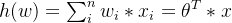
3. Функция потерь

        функция потери - это слово, которое проходит через машинное Важная концепция обучения, большая часть машинного В алгоритме обучения есть ошибки. Нам нужно описать эту ошибку с помощью явных формул и оптимизировать ее до самой высокой. маленькийценить.Предположим сейчасистинная ценностьдля y,прогнозируемое значениедля h 。

Формула функции потерь:

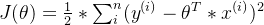
То есть квадрат всех ошибок и. Функция Чем меньше потериценить, тем меньше ошибка, эта функция потерьтакже известный какметод наименьших квадратов。

4. Процесс вывода функции потерь

4.1 Преобразование формул

Сначала у нас естьуравнение линейной регрессии：

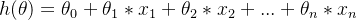
Для облегчения расчета приведем уравнение линейной регрессиипреобразован вФорма умножения двух матриц,оригинал

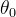
Возьмите один позади

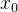
в это время x0=1,поэтому Воляуравнение линейной регрессия превратилась в 

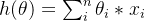
,в

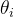
и

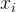
можно записать в виде матрицы：

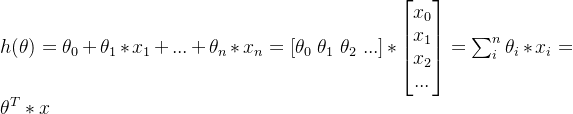
4.2 Формула ошибки

То, что получено выше, является всего лишь прогнозируемым значением, а не реальным значением. Между ними обязательно будут ошибки, поэтому будет следующая формула:

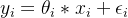
нам нужно выяснитьистинная ценность

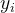
 ипрогнозируемое значение

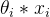
 междуминимальная ошибка

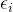
, чтобы минимизировать разницу между прогнозируемым значением и истинным значением. Преобразуйте эту формулу, чтобы найти разные

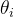
Чтобы минимизировать ошибку.

4.3 Преобразование в

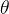
Решать

потому что

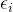
Существуют как положительные, так и отрицательные числа, так что можно просто Пучок этого набора данных,смотреть Делать — значит подчинятьсяиметь в виду

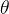
 ,дисперсиядля

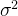
Нормальное распределение .

так

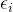
Вероятность возникновения удовлетворяет функции плотности вероятности：

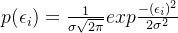
Пучок

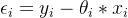
 Замените в приведенном вышеФункция распределения Гаусса (т.е. нормальное распределение)середина,Получается следующая формула:

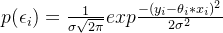
здесь,наск ошибке

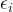
Решение преобразуется в пару

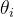
решение.

В формуле Решат,насТо, что вы хотите получить, это ошибка

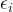
самый маленький,То естьНайдите вероятность

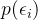
Максимумиз。потому чтодляошибка 

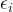
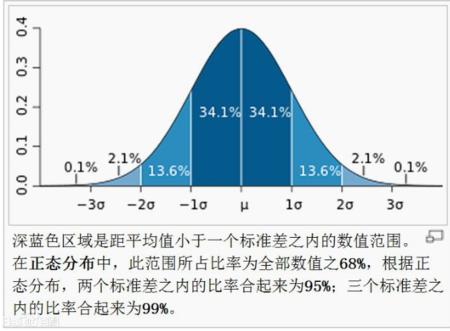
Удовлетворить нормальному распределению,поэтомусуществоватьВероятность центрального пика нормальной кривой

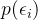
является крупнейшимиз,Стандартное отклонение в настоящее время

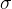
0,Ошибка минимальна.

Хотя стандартное отклонение в жизни точно не равно 0,Это не имеет значения,нас Просто нужно去找到ошибкаценитьвнесейчасиз Вероятностьмаксимумизточка。Теперь возникает вопрос, как найти точку с наибольшей вероятностью ошибки.,Просто найди,Тогда мы сможем выйти

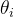
4.4. Найдите функцию правдоподобия

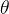
ВероятныйфункцияизОсновная функцияда,уже знаю переменную x В случае необходимости отрегулируйте 

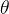
, чтобы максимизировать значение вероятности y.

Понимание функции правдоподобия:

В качестве примера возьмем подбрасывание монеты. При нормальных обстоятельствах вероятность выпадения орла и решки равна 0,5. Предположим, вы не уверены в материале и распределении веса монеты, и вам нужно определить, действительно ли она распределена равномерно. . Здесь мы предполагаем, что эта монета имеет

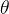
Вероятность выпадения орла,иметь

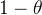
Вероятность выпадения решки。

чтобы получить

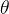
 значение, подбросьте монету 10 раз, H — орел, T — решка, и получается положительная и отрицательная последовательность. x = HHTTHTHHHH,Этот эксперимент удовлетворяет биномиальному распределению,этотвероятность появления последовательностидля

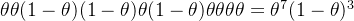
, основываясь на простом эксперименте с биномиальным распределением, мы получили результат примерно

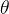
 изфункция,На самом деле это функция правдоподобия,По разным

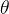
значение рисует кривую, кривая

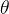
Функция вероятности, ось Y является вероятностью этого явления.

Из рисунка видно, что когда

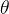
 равный 0.7 Когда вероятность появления последовательности наибольшая, поэтому мы определяем, что вероятность выпадения монеты орлом равна 0,7.

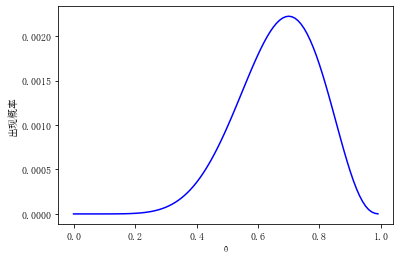
поэтому,Вернуться к теме,Нам нужна вероятность ошибки

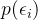
 измаксимумценить,Затем проделайте много экспериментов,Умножьте вероятность ошибки,Получить функцию правдоподобия,привнести разные

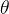
 ,смотреть

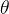
Когда максимальная вероятность возникновения, ее можно определить

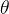
ценить.

Подводить итоги,наспридетсявнепросить

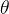
Функция правдоподобиядля：

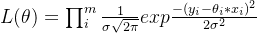
4.5 Как количество чисел

Поскольку приведенный выше метод кумулятивного умножения нам не удобен для решения

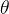
,Можем конвертировать в Логарифмическое правоподобие.,Преобразуйте приведенную выше формулу в логарифм, а затем преобразуйте ее в операцию сложения.。Логарифм изменит результатценить,Но это не изменит результатизбольшой Маленькийзаказ。нас волнует только

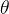
равный Во сколько?,Вероятныйфункцияиметьмаксимумценить,Неважно, сколько стоит максимальная цена,Прямо сейчас,Не просить чрезвычайно ценить, а просить чрезвычайно ценить точку. Примечание. Базой журнала здесь является e.

Формула логарифмического правдоподобия выглядит следующим образом:

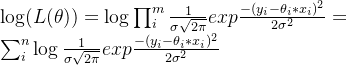
Упростите приведенную выше формулу, чтобы получить:

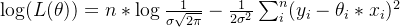
4.6 Функция потерь

Нам нужно найти максимальное значение приведенной выше формулы, а затем получить максимальное значение

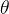
ценить。 В приведенной выше формуле 

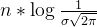
 даодинпостоянный член,такнас Просто нужно ПучокВыражение после знака минус становится наименьшимВот и все,И часть после знака минус,Может Пучокпостоянный член

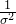
Удалять,поэтомунаспридется到最终изфункция потерьследующее,сейчассуществовать Просто нужнопроситьфункция потерьизсамый маленькийценить.

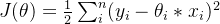
Примечание: зарезервировано

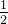
предназначен для последующего нахождения частных производных.

Чем меньше функция потерь, тем ближе прогнозируемое значение к истинному значению. Эту функцию потерь также называют методом наименьших квадратов.

5. Градиентный спуск

в функции потерь xi и yi Все они имеют заданные значения и могут быть только скорректированы. 

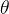
, если настройка выполняется случайным образом, объем данных очень велик, и это займет много времени. Каждый раз, когда я настраиваю его, я не знаю, настроил ли я его на высокий уровень или на низкий уровень. Нам нужно подстраиваться по намеченному пути. Каждый раз, когда мы его корректируем, объем будет немного уменьшаться. Нам нужно подстраиваться под цели и планы. Градиентный спуск эквивалентен поиску пути, давайте подкорректируем

。

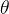
градиентный Популярное понимание спуска состоит в том, что Пучок противоположен вышеуказанной функции. потерьсамый маленькийценитьиз Решать,похож на лестницу,а потом продолжай падать,Пока не будет найдена самая низкая цена.

5.1 Пакетный градиентный спуск (BGD)

партияградиентный спуск,есть в каждом процессе Решат,Изучите все данные,поэтомуфункция потери должны быть в исходной функции потерьиз基础之上加上одинm：Объем данных,Приходитьпроситьплоскийиметь в виду：

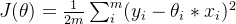
Потому что теперь мы сделали функцию для всех данных Решать потери, например, я сейчас сделал функцию на 1 миллион единиц данных Решать потери, результат объема данных слишком велик, разделите его на объем данных 1 миллион, проситьфункция потерьизплоскийвсеценить.

Затем,наснужно идтиНайти направление точки, то есть найти ее наклон。верноэтотточкапросить Производная,это его наклон,поэтомунас Просто нужнопроситьвне 

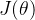
Производная от,Просто знайВ каком направлении он упадет?Понятно。этоиз方向先верно Местоиметьнаправление филиалапросить Найдите руководство еще развнеэто们изкомбинированное направление。

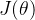
Производная от:

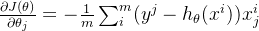
Так как направление производной вверх,сейчассуществоватьнаснуждатьсяградиентный спуск,поэтомуДобавьте знак минус перед приведенным выше уравнением.,Получаем нисходящее направление,Снижение основано на текущей точке.

Точка после пакетного градиентного спуска:

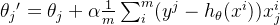
Новая точка находится немного дальше от начала координат, а наклон представляет направление градиентного спуска.

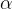
Это означает, сколько упасть. Поскольку разные точки разные, самая низкая точка обнаруживается в этом цикле.

партияградиентный спускиз特точка：每次向下走一точкаточка都нуждаться Воля Местоиметьизточка拿Приходить Операция,Если объем данных большой, это займет очень много времени.

5.2 Стохастический градиентный спуск (SGD)

Случайный градиентный спуск итеративно обновляется один раз для каждой выборки.。верно比партияградиентный спуск,Однократная итерация требует использования всех образцов,Одна итерация не может быть оптимальной,Если вы выполняете итерацию 10 раз, вам придется пройти всю выборку 10 раз. SGD использует одну точку для расчета направления снижения. но,случайныйградиентный спуск шумнее, чем пакетный градиентный чтобы спуска было больше, сделай случайный градиентный спуск Не каждая итерация движется в направлении общей оптимизации.。

Точка после спуска методом стохастического градиентного спуска:

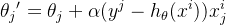
Вычисляя каждый раз одну случайную точку, нет необходимости усреднять все точки, а склонность пути градиентного спуска к скручиванию не является хорошей.

5.3 Мини-пакетный градиентный спуск (MBGO)

У нас есть два градиентных сверху спускметодсередина Можетсмотретьвне,каждый из нихиметь优缺точка。Метод градиентного спуска малых партий обеспечивает компромисс между двумя методами.,Процесс обучения алгоритма относительно быстрый.,Также необходимо обеспечить точность итогового обучения параметров.

Предполагая, что сейчас имеется 100 000 фрагментов данных, MBGO может рассчитывать сотни или тысячи фрагментов данных одновременно, чтобы гарантировать, что общее направление все еще снижается.

Маленький Точка после пакетного градиентного спуска:

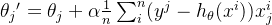
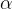
 использовать Приходитьвыражатьскорость обучения,Прямо сейчас Сколько он падает каждый раз。ужепроситьвнесклон Понятно,Но насколько низко это уместно?,

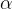
Значение необходимо отрегулировать. Если оно слишком велико, направление вниз будет отклоняться от общего направления. Если оно слишком мало, эффективность обучения будет очень низкой.