Легкий 3D-лидар реального времени SLAM для автономного вождения в крупномасштабных городских условиях
оригинальный:Легкий 3D-лидар реального времени SLAM для автономного вождения в крупномасштабных городских условиях

00 краткое содержание
Для автономных транспортных средств очень важно позиционирование и картографирование в реальном времени в неизвестных условиях. В этой статье предлагается быстрый и легкий 3D-лидар SLAM для локализации автономных транспортных средств в крупномасштабных городских условиях. В этой статье предлагается новый метод кодирования, основанный на информации о глубине, который может кодировать неупорядоченные облака точек с различным разрешением, избегая потери размерной информации, когда облако точек проецируется на двумерную плоскость. Анализ главных компонентов (PCA) модифицируется путем динамического выбора точек соседства на основе закодированной информации о глубине, чтобы соответствовать локальным плоскостям с меньшими затратами времени. Порог и количество характерных точек адаптируются в зависимости от интервала расстояний, поэтому редкие характерные точки извлекаются и равномерно распределяются в трехмерном пространстве. Извлеченные ключевые характерные точки повышают точность одометрии и ускоряют выравнивание облаков точек. Эффективность и надежность алгоритма проверены на KITTI и MVSECD. Спидометр оценил быстрое время работы в 21 мс. По сравнению с несколькими типичными современными методами KITTI предлагаемый метод снижает ошибку перевода как минимум на 19%, а ошибку вращения - на 7,1%.
01 Введение
Будучи одной из основных технологий автономного вождения [1], позиционирование и навигация транспортных средств всегда были предметом исследований. Этот алгоритм должен обрабатывать большой объем данных [2], и особенно важны облегченные алгоритмы. Эти технологии представляют огромную ценность для автомобильной промышленности [3]. Позиционирование и навигация обычно могут быть достигнуты с помощью карт HD и GPS. Однако карты HD и GPS подходят не для всех городских сценариев, таких как туннели, эстакады, экранирование высотных зданий и перебои в обслуживании, вызванные техническими проблемами. При отсутствии карт высокого разрешения и GPS локализацию можно решить путем оценки собственного движения SLAM. Стабильные технические алгоритмы могут обеспечить безопасность автономного вождения [4]. SLAM может решить задачу оценки положения транспортных средств в неизвестной среде и построить карту окружающей среды. В зависимости от используемого датчика (камера, лидар) этого обычно можно достичь с помощью визуального SLAM [5], [6], [7] и лидарного SLAM [8], [9], [10], [11], [ 12] Классифицируйте это. Visual SLAM пассивно получает информацию от камеры и сильно зависит от освещения и текстур окружающей среды. Напротив, 3D LiDAR SLAM опирается на активное измерение LiDAR геометрической информации окружающей среды, а не информации о текстуре. Таким образом, LiDAR SLAM более стабилен и широко используется в практических целях на открытом воздухе. Полная лидарная система SLAM включает в себя интерфейсную одометрию для оценки ориентации и внутреннюю оптимизацию глобальной карты ориентации. Регистрация облака точек — это ядро интерфейса, из которого можно получить данные о положении автомобиля. Типичные методы включают итерационный метод ближайшей точки (ICP) [13], преобразование нормализованного распределения (NDT) [14] и методы, основанные на признаках. Классический ICP объединяет ближайшие точки на основе евклидова расстояния и постоянно итеративным образом оптимизирует соответствие между точками для получения преобразования движения транспортного средства. Однако преобразование каждой пары точек в облаке точек кадра требует большого объема вычислений. NDT делит облако точек на множество небольших сеток, а затем вычисляет распределение вероятностей между сетками. Непрерывно дифференцируемые плотности вероятности используются для оценки автономного движения между последовательными кадрами LiDAR. Однако этот алгоритм чувствителен к углу поворота, а на точность регистрации влияет размер сетки. Методы, основанные на функциях, извлекают только облака точек с функциями для сопоставления, чтобы добиться превосходной производительности в реальном времени и высокой точности. Однако методы извлечения признаков для автономных транспортных средств остаются проблемой в городских сценах, где геометрические особенности неочевидны.
На основе вышеперечисленных методов было предложено несколько методов SLAM для наружного 3D-лидара. LOAM [8] предложил регистрацию облаков точек по принципу «точка-линия» и «точка-лицо» на основе характерных точек для достижения точной одометрии. Однако из-за отсутствия серверной оптимизации это приводит к значительному отклонению в крупномасштабных средах с небольшим количеством геометрических особенностей. LeGO LOAM [9] предлагает быстрый и легкий метод SLAM, который использует наземную оптимизацию, но отсутствие облака наземных точек приведет к большему количеству ошибок в одометрии. HDL_GRAPH_SLAM [10] представляет собой 3D-лидарную структуру SLAM, основанную на графической оптимизации с циклом, которая может интегрировать IMU, GPS, дорожные ограничения и т. д., но метод регистрации облака точек от сканирования к сканированию для предварительной одометрии не является точным. достаточно. LIOM [11] предложил надежный инерциальный метод одометрии и картографирования LiDAR с низким дрейфом в крупномасштабных быстродвижущихся средах, но он занимал большой объем памяти и имел низкую производительность по времени. Эти решения все еще имеют недостатки в крупномасштабных городских условиях.
В этой статье мы сосредоточимся на надежной локализации и картографировании автономных транспортных средств в режиме реального времени в сложных крупномасштабных городских условиях. Количество входных облаков точек можно уменьшить, удалив точки земли на основе подгонки плоскости. Предварительно обработанное неупорядоченное облако точек затем кодируется на основе информации о глубине, а не проецируется на 2D-плоскость. Путем улучшения PCA предлагается надежный двойной адаптивный алгоритм извлечения признаков, основанный на закодированной информации о глубине. Положение транспортного средства оценивается путем регистрации извлеченных краев и точек плоскости. Наконец, двухэтапное обнаружение цикла используется для оптимизации глобального графа и устранения накопленных ошибок. Эффективность и надежность нашей системы были проверены на наборах данных KITTI [15] и MVSECD [16]. Основные положения этой статьи заключаются в следующем:
- Информация о глубине используется для кодирования неупорядоченных облаков точек, что позволяет избежать потери информации о размерах, вызванной проецированием облаков точек на двумерную плоскость. Это кодирование работает для различных разрешений облака точек без необходимости сортировки облака точек по слоям.
- Усовершенствован метод выбора точек соседства в PCA. Точки выбираются динамически в соответствии с закодированной информацией о глубине для соответствия локальной плоскости. По сравнению с выбором фиксированной точки в исходном PCA, временные затраты алгоритма могут быть эффективно сокращены.
- Предлагается метод адаптивного выбора порогов и количества характерных точек в пределах разных интервалов расстояний. По сравнению с традиционными методами извлечения признаков с фиксированным числом этот метод извлекает более однородные разреженные характерные точки в трехмерном пространстве, тем самым повышая точность одометрии и сокращая временные затраты.
02 Связанная работа
В 3D-лидаре SLAM оценка ориентации в основном осуществляется посредством регистрации облаков точек между кадрами. Регистрация общедоступного облака точек в SLAM включает в себя прямую регистрацию ICP [13] и регистрацию характерных точек. ICP не нужно сортировать входное облако точек, ему нужно только найти ближайшую точку для регистрации, но регистрация каждой точки занимает много времени. Методы, основанные на характерных точках, требуют сортировки входного неупорядоченного облака точек, но их можно быстро зарегистрировать.
Классическая итерация ICP решает задачу двухточечного преобразования. Чтобы повысить скорость и точность регистрации облака точек, расстояние от точки регистрации до плоскости используется в качестве меры ошибки, а точки сопоставляются с локальной плоскостью. GICP [17] модифицировал модель потерь путем сопоставления двух локальных плоскостей путем комбинирования методов ICP «точка-плоскость» и «плоскость-плоскость». IMLS-SLAM [18] предлагает метод выравнивания модели пары точек, основанный на неявном скользящем методе наименьших квадратов, который выравнивает точки выборки с неявной поверхностью путем извлечения наблюдаемых точек выборки. Эти усилия в определенной степени улучшили ICP, но производительность в реальном времени по-прежнему будет ухудшаться при обработке больших объемов данных облака точек.
В отличие от метода ICP, метод характерных точек регистрирует только небольшое количество извлеченных характерных точек, поэтому скорость регистрации высокая. LOAM [8] — это классический наружный 3D-лидар SLAM, в котором впервые предложен метод, основанный на регистрации характерных точек. Сортирует входное облако точек в соответствии с угловым разрешением лидара. LOAM вычисляет гладкость нескольких соседних облаков точек на одном и том же пучке прямых линий для извлечения краевых элементов и элементов плоскости, а также оптимизирует остаточные расстояния между точками и линиями и между точками и плоскостями для получения одометрических поз. На основе LOAM компания LeGO LOAM [9] предложила легкую систему SLAM. Он сортирует входные неупорядоченные облака точек, проецируя их на изображения на расстоянии. Затем двухэтапная нелинейная оптимизация L-M выполняется на сегментированных наземных точках и краевых точках, и последовательно решаются коэффициенты преобразования двух наборов облаков точек. Однако проецирование облака точек на двумерную плоскость приведет к потере одного измерения информации. Lio-sam [19] представляет собой метод слияния точек на основе признаков, который объединяет данные IMU и GPS, но требует совместной калибровки датчиков. F-суглинок [20] выделяет одинаковое количество характерных точек на разных расстояниях, как и в вышеупомянутых работах. Вместо итеративной компенсации искажений используется неитеративная двухэтапная компенсация искажений, что обеспечивает высокую вычислительную эффективность и точность ориентации. MULLS [21] предложил многомасштабный линейный итеративный алгоритм наименьших квадратов, основанный на классификационных признаках точек.
Метод главных компонентов (PCA) используется для извлечения шести мелких особенностей, включая точки земли, фасад, столб крыши, балку и вершину. Классификация характерных точек используется для регистрации ICP «точка-точка», «точка-линия» и «точка-плоскость», чтобы получить универсальную систему LiDAR SLAM с низким дрейфом.
03 Введение в структуру
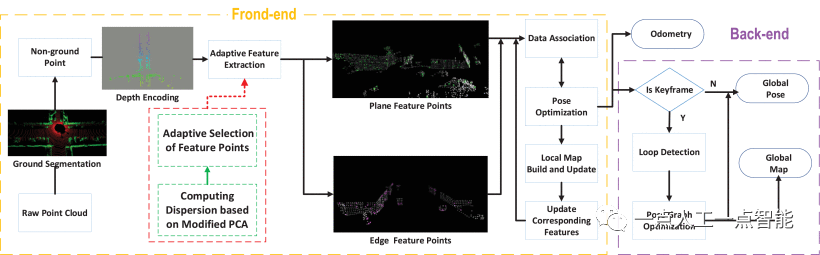
Структура системы, предложенная в этой статье, показана на рисунке 1, на котором внешний интерфейс получает данные облака точек от датчика и предварительно обрабатывает исходное облако точек для сегментации наземных точек. Сортировка неземных точек с использованием информации о глубине. Извлекайте краевые и плоские элементы из неосновных точек с помощью методов адаптивного извлечения. На основе совмещения характерных точек в двух последовательных кадрах получается относительное положение движения транспортного средства. Одометр транспортного средства можно оценить путем накопления относительного положения с течением времени. Серверная часть получает информацию о местоположении от одометра и определяет, достигло ли транспортное средство своего предыдущего местоположения. Наконец, методы оптимизации на основе графов используются для устранения ошибок в процессе сопоставления и получения глобально согласованных траекторий и картографирования.
04 Знакомство с методом
4.1 Наземная сегментация
Наземные точки обычно составляют большую часть трехмерного облака точек, записываемого автономными транспортными средствами. Выполняя наземную сегментацию входного облака точек, количество облаков точек можно уменьшить. Традиционные методы наземной сегментации включают RANSAC [22] и лучевой наземный фильтр [23]. RANSAC оценивает параметры модели на основе случайных выборок наблюдаемых данных. Алгоритм фильтрации лучей на земле рассчитывает изменение радиуса точки под тем же углом для получения точек земли. Однако приведенный выше алгоритм случайным образом выбирает точки из всего облака точек, что приводит к медленному времени работы и ошибкам сегментации.
В этой статье мы применяем метод быстрой наземной фильтрации [24], который выбирает набор исходных точек в качестве априорного значения для ускорения алгоритма.
первый,Кадр облака точек разделен на n сегментов вдоль направления движения транспортного средства. Область в направлении оси X разделена на несколько подплоскостей. Объединение нескольких подпланов в одну плоскость,Чтобы уменьшить ошибки сегментации, вызванные изменениями уклона земли. Затем,Выбираем точки по оси Z с меньшими значениями,и вычислить их средний ростH_m 。th_z Относится к пороговому значению для выбора начальных точек.。На данный моментz Значение меньше порогаH_m+th_z час,Выберите эту точку в качестве набора исходных точек.S \in \mathbb{R}^3 。Исходная точка используется как приоритетная точка начальной плоскости.,Используется для ускорения подгонки плоскости. Набор исходных точек помещается в исходную плоскость. Рассчитайте расстояние поперечной проекции между каждой точкой и исходной плоскостью. Как показано на рисунке 2(а),Если расстояние меньше искусственного порогаth_g , то точка будет считаться наземной точкой (т.е. ground point)。

Математическое выражение, используемое для оценки планарной модели, выглядит следующим образом:
ax+by+cz+d=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)
Представлено в векторной форме:
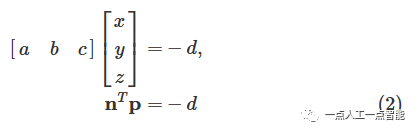
\pmb{\text{n}} По ковариацииM\in \mathbb{R}^{3\times3} Решать,M Опишите дисперсию набора исходных точек каждого субрегиона:
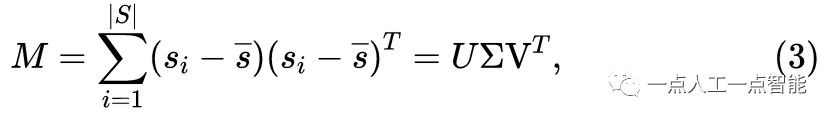
в\bar{s}\in \mathbb{R}^3 все точкиs_i \in \mathbb{R}^3 среднее значение,s_i \in \mathbb{R}^3 ,U \in \mathbb{R}^{3\times 3} ,V = MM^T ,V\in \mathbb{R}^{3\times3} ,\Sigma = \text{diag}(\sigma_1,\sigma_2,\sigma_3) 。Нормальный\pmb{\text{n}} перпендикулярно плоскости,Указывает направление минимального отклонения.。параметрd Это можно сделать, преобразуя уравнение(1)в\pmb{\text{p}} Заменить на\bar{s} Приходить Решать。Путем вычисления перпендикулярного расстояния между каждой точкой и исходной плоскостью,с порогомTh_{dist} Сравните его, чтобы определить, принадлежит ли он следующему самолету. Наконец, все классифицированные наземные точки используются в качестве исходных точек на следующей итерации для итеративной оптимизации. На рисунке 2(b) показано объединенное в подплоскостях облако наземных точек с использованием описанного выше алгоритма.
4.2 Упорядоченное кодирование облака точек
Входные данные, полученные от LiDAR, обычно представляют собой неупорядоченное трехмерное облако точек, которое можно преобразовать в организованную последовательность облаков точек путем проецирования на двухмерную плоскость или классификации на основе угловой информации. Здесь информация о глубине используется для сортировки неупорядоченного входного облака точек, что позволяет избежать потери информации о размерах или зависимости от разрешения лидара. 3D scanразделены на равные интервалы в радиальном направлении координат датчикаN_r Кольцо. Количество колец рассчитывается следующим образом:
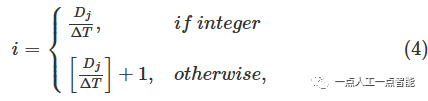
где [⋅] — символ округления,\Delta T - расстояние радиального зазора между различными кольцами,D_j каждое облако точек, не являющееся наземным,p^N_j(x_j,y_j,z_j) информация о глубине,Зависит отD_j=\sqrt{x_j^2+y^2_j+z^2_j} вычислить。Когда интервал слишком великчас,Характерные точки распределены редко.,Это влияет на точность одометра. в этой статье,мы используем\Delta T=4\ m иN_r=21 。В зависимости от значения расстояния каждой точкиD_j ,точкаp^N_j разделен на соответствующие кольцаN_j (Как показано на рисунке 3). Подмножество облака точек для каждого кольца представлено следующим образом:
\rho=\bigcup_{i \in\left[N_{r}\right]} \rho_{i}\ \ \ \ \ \ \ \ (5)
в\rho_iпринадлежит кiкольцаизточканабор,N_r=[1,2,...,N_{r-1},N_r] 。
После разделения облака точек,каждое кольцоR(i) Подмножество облака точек выражается как:

поэтому,Воляточка Облака классифицируются как имеющие разные индексы расстояния.D_{id} сбор и выполнение дальнейшей обработки облака точек на основе этого индекса.
4.3 Расчет дисперсии на основе улучшенного PCA
Поскольку в процессе регистрации нет совпадающих точек, точки с единичными значениями в неземном облаке точек оказывают негативное влияние на точность позиционирования одометрии. Следовательно, перед извлечением признаков необходимо удалить точки сингулярного значения. Путем кластеризации неземных точек для классификации объектов используется метод евклидовой кластеризации. Когда количество кластеризованных облаков точек меньше порогового значения, выбросы классифицируются и удаляются. Удаление выбросов перед извлечением признаков может уменьшить количество избыточных точек и повысить осуществимость характерных точек.
LOAM [8] предложил метод извлечения признаков.,Для расчета локальной гладкости нескольких соседних точек одной балки. но,Поскольку значения плавности равны,Может выйти из строя в случае геометрической деградации. Чтобы повысить надежность алгоритма извлечения признаков,Алгоритм анализа главных компонент (PCA) улучшен для извлечения особенностей облака точек. В исходном алгоритме PCA,Подберите локальную плоскость, используя фиксированное количество точек окрестности. Мы адаптивно выбираем точки окрестности по интервалам расстояний, чтобы они соответствовали локальной плоскости.,тем самым улучшая метод。Районточкаk определение количествадля:k=\alpha -[\beta D_{id}(i)] ,в[⋅]это символ округления,αиβда Линейныйпараметр。Чтобы сократить вычислительные затраты на поиск,Воляточка Облачное хранилище в3D в дереве КД. Используя эти точки окрестности, дисперсия локальных доменов (The local domain dispersion)。выбраноиз Районточкаp_i(x_i,y_i,z_i) Расстояние от местного центра составляет:
\partial _i =p_i-\frac{1}{k}\sum^{k}_{j=1}p_j=[\partial_{ix},\partial_{iy},\partial_{iz}] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7)
вk да Районточкаизобщий,i=1,2,3,...,k 。Затем рассчитайте его по следующей формулеk Ковариационная матрица точек:
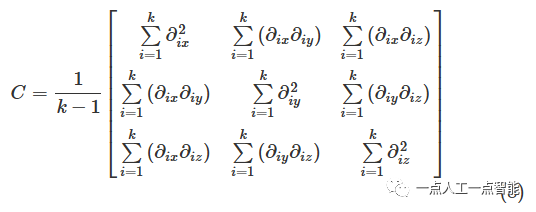
ковариационная матрицаCсобственные значения\lambda_i=(i=1,2,3) ипереписыватьсясобственный вектор\mathbb{N}_i(i=1,2,3) через разложение по сингулярным значениям(SVD)Конечно。Отсортируйте собственные значения, чтобы получить\lambda_1>\lambda_2>\lambda_3 。соответствует максимальному собственному значению\lambda_1 собственный вектор\mathbb{N}_1 является основным вектором,соответствует\lambda_3 собственный вектор\mathbb{N}_3 это нормальный вектор. Эти собственные значения и собственные векторы можно использовать для извлечения краевых и плоских особенностей локальных облаков точек. Согласно соотношению между собственными значениями локальную линейность и планарность можно определить как [25]:

в\delta это плоскостность,\epsilon линейность。в соответствии с\delta и\epsilon изфункция выбора значенияточка。с оригиналомPCAметод по сравнению,улучшенныйPCAАлгоритмы ускоряют извлечение признаков。использовать Районточка(k=\alpha - [\beta D_{id}(i)],\alpha=10,\beta=0.1) изадаптивный отбориз Коэффициент извлечения функций фиксированточка(k=5) на 4 мс быстрее.
4.4 Адаптивный выбор характерных точек
в целом,Порог выбора характерных точек и количество характерных точек фиксированы (например,,Ссылка [8] выбирает 20 краевых точек). Однако,Облака точек, полученные в результате лидарного сканирования, на больших расстояниях редки.,плотный на близком расстоянии,Это приводит к неравномерному распределению характерных точек. Неравномерное распределение отрицательно влияет на точность одометрии и стабильность системы SLAM. поэтому,Мы предлагаем метод адаптивного выбора характерных точек на основе расстояния. Согласно разделу 4.3,Получите каждыйточкаоблакоизиндексD_{id} 。в соответствии срасстояние间隔自适应地вычислитьособенностьточкавыбиратьизпорог\mathcal{X} для:
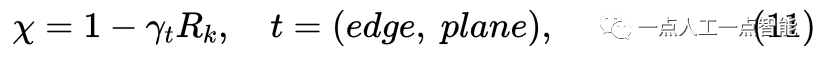
вk дакаждыйточкаизрасстояние,R_k да По уравнению(4)количество полученных расстоянийk диапазон,\gamma является линейным фактором. Обычно из-за особенностей позынужно большеизплоскийточка,\gamma плоскийиз Установлено значение больше, чем\gamma край. Такие как Рисунок 4показано,Согласно уравнениям (9) и (10),Получено путем сравненияизпороги局部色散值Приходитьвыбирать边缘p_{\varepsilon} иплоскийp_s Особенности:
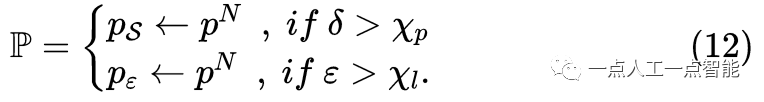
безразличныйизрасстояние间隔中动态выбирать不同数量изособенностьточка。особенностьточкаиз Адаптивные величины выражаются математически.для:num=\omega_tR_t,\omega<1 ,numцелое число。нравиться Рисунок 5показано,Характерные точки, полученные методом адаптивного выбора, более редки, чем точки, полученные методом фиксированного выбора. Извлеченные характерные точки равномерно распределены по шести степеням свободы. Равномерно распределенные характерные точки в шестимерном пространстве накладывают ограничения на каждую степень свободы.,И улучшить точность одометра и стабильность системы SLAM. Полный процесс алгоритма извлечения признаков показан в алгоритме 1.


4.5 Обновление модели
Оценка позы заключается в выравнивании текущих характерных точек края и характерных точек плоскости в наземных координатах глобальной карты. Для ускорения поиска соответствующих точек,Воля边缘иплоскийособенностьточкахранится вKDсреди деревьев。Наземная система координат обозначена как\text w ,Маркеры системы координат LiDAR\mathcal{L} . Отношения перехода состояний транспортного средства можно выразить как:

С помощью алгебры Ли преобразование состояния шести степеней свободы выражается следующим образом:
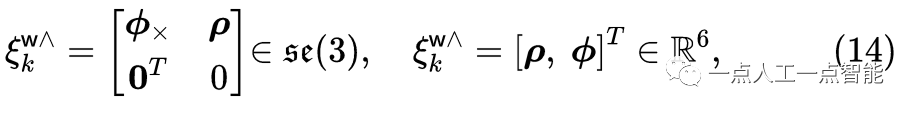
в\rho и\phi представляют собой соответствующий сдвиг и вращение в касательном векторе соответственно,
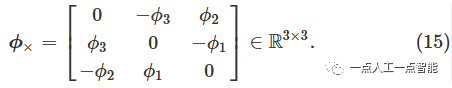
Алгебра Лии Ли Цюнь Сопоставление по индексуи Преобразуйте логарифмическую карту[24]。Ли ЦюньT^{\text w}_{\mathcal{L}}=[\pmb{R,t}] \in SE(3) Преобразование содержит матрицу вращения\pmb{R}\in SO(3) ивектор перевода\pmb{t}\in\mathbb{R}^3 . Связь между матрицей вращения и вектором перемещения:
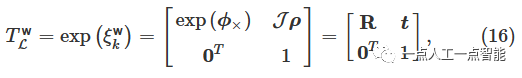
в\mathcal{J} – матрица Якобиана [26], и ее определение таково:
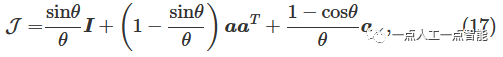
\thetaда\xi^{\text w}_k Длина модуля,\pmb{a} да\xi^{\text w}_k вектор направления,Длина равна 1,||\pmb{a}||=1 。
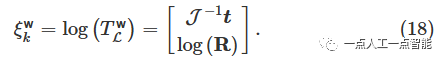
Модель обновления статуса автомобиля выглядит следующим образом:
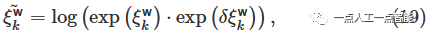
\delta \xi^{\text w}_kда Получено путем непрерывной итеративной оптимизации.изприращение отношения。
4.6 Оценка отношения
Воляточкаоблако转换为同一坐标系以估计里程计姿态。краевые особенности\mathbf {p}_{\varepsilon k}^{\ell} \epsilon \mathbb{P} Преобразовать в наземную систему координат\tilde{\mathbf{p}}_{\varepsilon k}^{\text w} 。Необходимо найти два края в наземной системе координат.точка(\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {a}}},\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {b}}}) 。эти двоеточкасоединить по прямой,для построения точечных остатков. первый,Найдите пять близлежащих краевых точек в наземной системе координат. Затем,Локальный центр пяти точек рассчитывается согласно уравнению (7). наконец,использовать\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {a}}} выбирать中心前面източка,использовать\pmb {\text {p}}^{\pmb {\text {w}}}_{\pmb {\text {b}}} Выберите следующие пункты. Уравнение невязки расстояния от точки до прямой строится следующим образом:
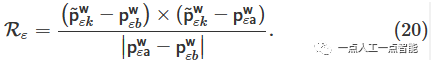
Сходным образом,Воляплоскийособенностьточка\mathbf {p}_{S k}^{\ell} \epsilon \mathbb{P} Преобразовать в мировую систему координат\mathbf {p}_{S k}^{\tilde{\text w}} 。Найдите три близлежащие точки в наземной системе координат.изплоскийточка(\mathbf {p}_{S t}^{\text w},\mathbf {p}_{S u}^{\text w},\mathbf {p}_{S v}^{\text w}) для образования ровной поверхности. Остаточное уравнение для расстояния от точки до плоскости имеет следующий вид:
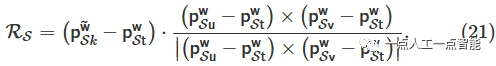
Мы объединяем линейные и плоские остатки, чтобы получить оптимизированную по позе функцию потерь следующим образом:
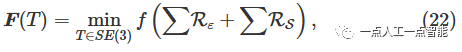
Метод Гаусса-Ньютона используется для решения задач нелинейной оптимизации. Выполните разложение Тейлора первого порядка,Решать Приращениенравиться Внизf(x+\Delta x)\approx f(x)+\mathcal{J}(x)\Delta x . Инкрементное уравнение переписывается следующим образом:

здесь\mathcal{J} да Якобиматрица,\mathcal{H} даопределяется как\mathcal{H}=\mathcal{J}(x)\mathcal{J}^T(x) Матрица Гессе,Δxда Приращение,g=-\mathcal{J}(x)f(x) 。Преобразуйте нелинейные проблемы в итеративные приращения решенияΔx。предельный остатокиз Якобиматрица\mathcal{J}_{\varepsilon } Его можно рассчитать по следующей формуле:
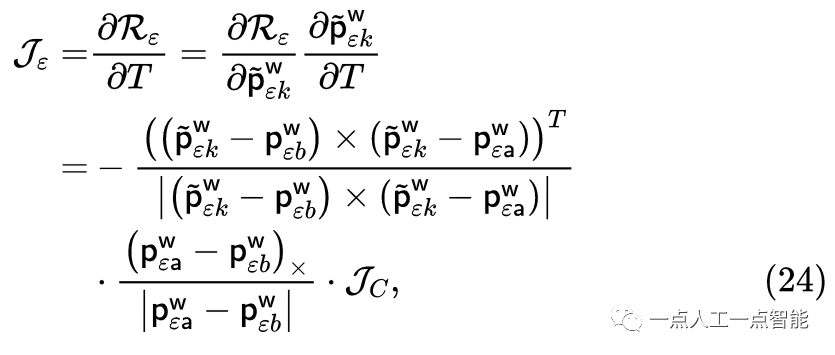
может пройтииспользовать\delta \xi \epsilon \mathfrak{s e}(3) Левая модель возмущения ( left perturbation model)Приходить估计Якобиматрица\mathcal{J}_C :
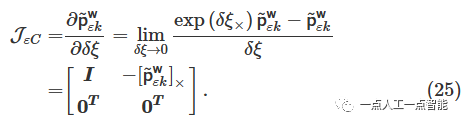
Аналогично можно получить плоскую матрицу Якобиана:
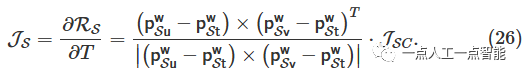
Инкрементное уравнение решается с помощью матрицы Якоби, где приращение итеративно оптимизируется до тех пор, пока уравнение не сходится.
4.7 Оптимизация серверной части
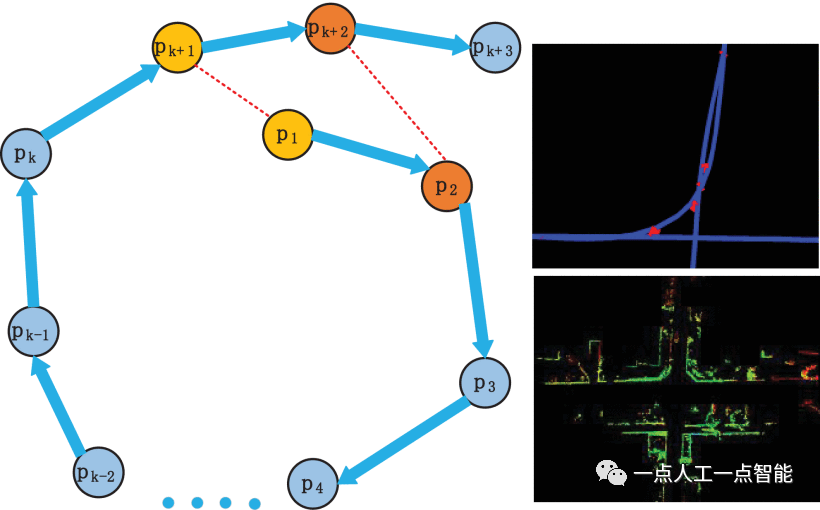
Со временем в одометрии накапливаются ошибки, что приводит к ухудшению глобального картографирования. Кумулятивные ошибки можно устранить за счет глобальной оптимизации обнаружения и сопоставления петель. Чтобы ускорить оптимизацию карты, мы применяем подход на основе ключевых кадров во время обнаружения циклов и глобальной оптимизации. Когда изменение позы между двумя кадрами превышает определенный порог, текущий кадр выбирается в качестве ключевого кадра. Кадры, подобные текущему, исключаются из ключевых кадров истории. Относительные положения двух похожих кадров добавляются в оптимизацию графа как ограниченные ребра. Мы используем двухэтапный подход к обнаружению петель. Во-первых, используется быстрый и эффективный метод обнаружения цикла для сканирования информации до и после [27] для поиска кадров-кандидатов на замыкание цикла из исторических ключевых кадров. Введен дескриптор, инвариантный к вращению, для сканирования информации до и после, чтобы быстро обнаружить циклы, происходящие в разных направлениях. Затем ICP используется для сопоставления текущего кадра с кадром-кандидатом для получения оценки между двумя кадрами. Как показано на рисунке 6, если оценка меньше заданного порога, в двух кадрах возникает цикл. Относительные положения между двумя кадрами цикла добавляются в качестве ребер ограничений в систему оптимизации графа GTSAM [28]. Эта система оптимизации может эффективно оптимизировать картографирование и устранить накопленные ошибки. Исторические места и глобальные карты обновляются соответствующим образом.
05 Экспериментальная оценка
5.1 Проверка переднего одометра в KITTI
Впервые мы проверили точность и эффективность предварительной одометрии в предлагаемой системе на тесте одометрии KITTI [15]. В тестах использовались только лидарные данные. Набор данных собирается из больших и сложных сцен, включая городские, сельские и шоссейные. Для оценки алгоритма была выбрана последовательность 00-10, которая обеспечивает основные значения истинности. Всего 23201 кадр в 11 последовательностях и длина трека 22км. Проверьте точность вашего одометра, используя индикаторы одометра, предоставленные KITTI. Ошибки перемещения и вращения рассчитываются для разных длин, в частности, каждые 100–800 м. Средние значения ошибок ARE и ATE, определенные эталоном одометра KITTI, представляют собой среднюю ошибку вращения и среднюю ошибку трансляции соответственно. Чем меньше значение, тем выше точность алгоритма.
![Таблица 1 Сравнение оценок лидарной одометрии с набором данных KITTI. Все ошибки выражаются как ATE[%]/ARE[°/1m] (чем меньше, тем лучше). Не все методы используют обнаружение замыкания цикла.](https://developer.qcloudimg.com/http-save/10091650/e4c7f527246be66ba4866b1e804c97c7.png)
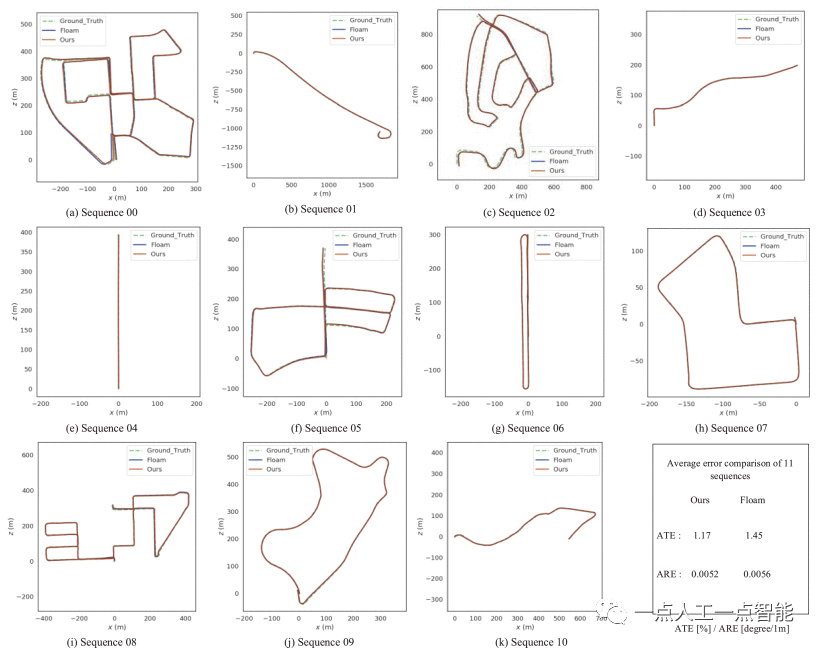
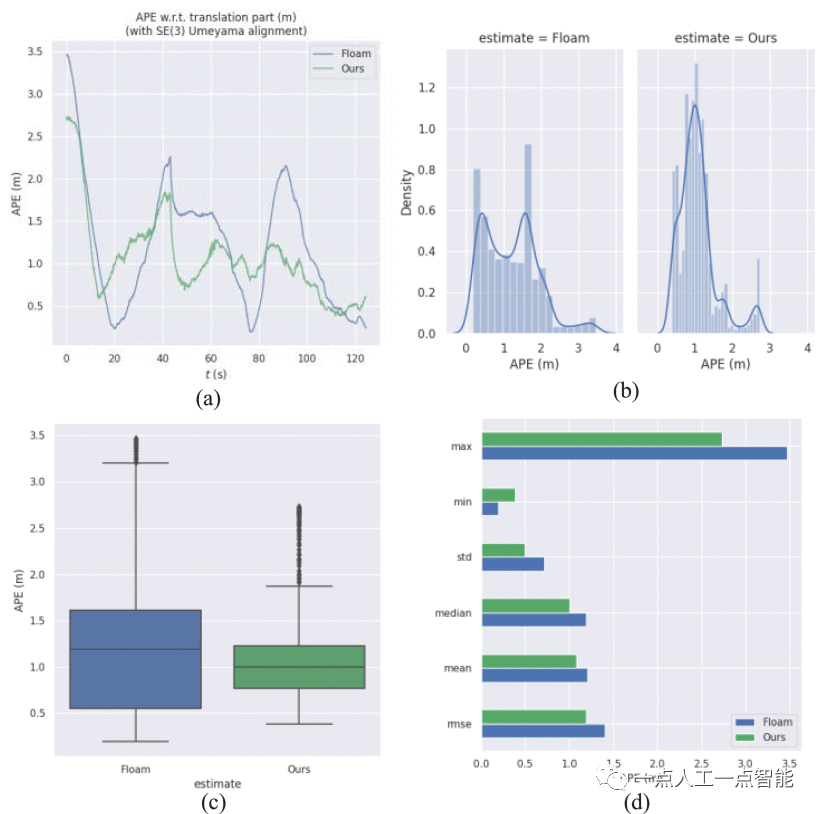
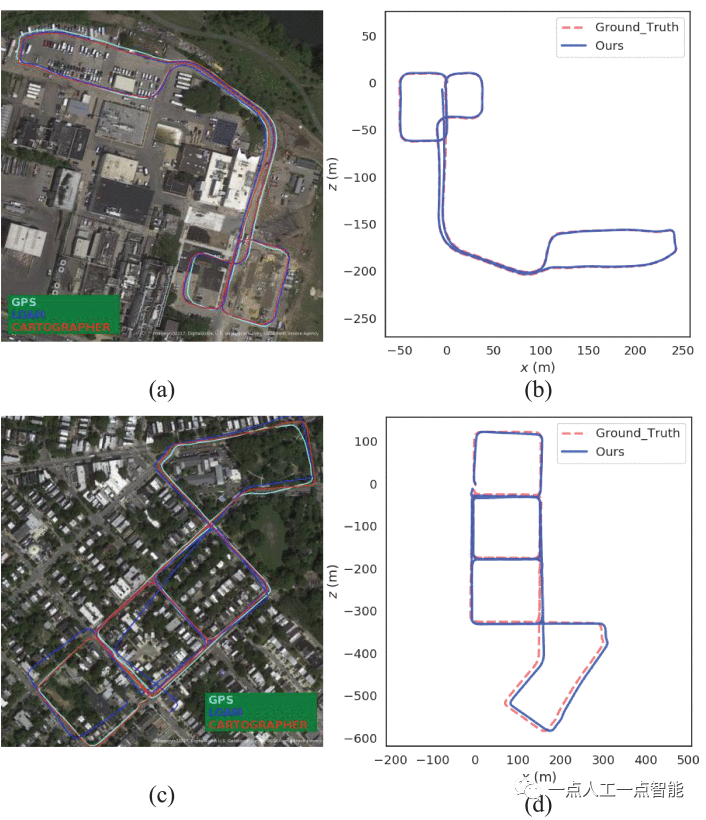
Предложенный метод одометрии (без использования обнаружения петель) сравнивается с современным алгоритмом определения траектории FLOAM. На рисунке 7 показано сравнение трех траекторий нашего алгоритма, FLOAM и основной истины на 11 последовательностях. Красная сплошная линия — это траектория нашего алгоритма, синяя сплошная линия — это траектория одометра FLOAM, а зеленая пунктирная линия — это основная истина GPS/INS. Так как предложенный алгоритм убирает некоторые лишние моменты. Извлеченные характерные точки более равномерно распределены по шести степеням свободы. Следовательно, наш алгоритм ближе к реальности, чем FLOAM, на большинстве последовательностей. Все траектории по существу соответствуют истине. На рисунке 8 показана точность предложенной оценки одометрии. Мы сравниваем абсолютную ошибку ориентации (APE), оцененную с помощью одометрии между FLOAM и предложенным алгоритмом. APE предлагаемого алгоритма меньше, чем FLOAM, и наш алгоритм более точен. Диапазон колебаний ошибки меньше, и наша система более стабильна. Предлагаемый алгоритм также меньше, чем FLOAM, по другим показателям оценки, включая среднеквадратическую ошибку (RMSE) и стандартное отклонение (STD). Эксперименты показали, что алгоритм способен точно позиционировать себя в крупномасштабных городских условиях.
5.2 Эксперимент по обеспечению устойчивости системы SLAM
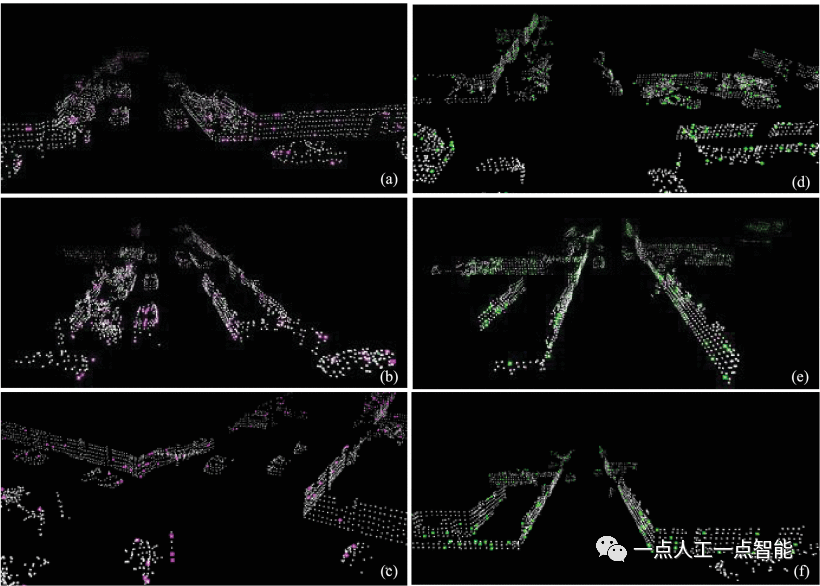
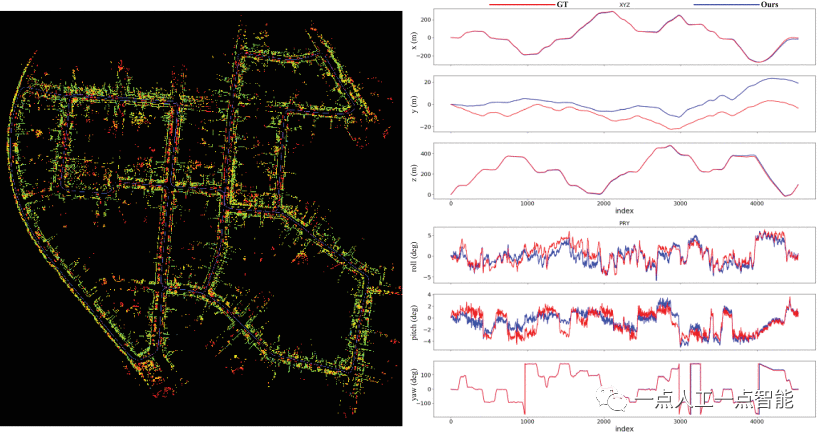
Мы выбрали для анализа три типичные последовательности городских сцен 00, 05 и 07 из одометрического теста KITTI. На рисунке 9 показаны результаты картографирования, созданные системой SLAM в большой городской среде с последовательностью KITTI 00, а также ошибки в картографировании положения и ориентации. Предложенный алгоритм способен обрабатывать описанные выше сценарии перемещения объектов. Алгоритм имеет небольшие ошибки позиционирования в направлениях x, y и рыскания. Как показано на рисунке 9, 2D-компоненты ориентации по координатам x, y и рысканию близки к земле, хотя имеются некоторые ошибки в направлениях высоты, крена и тангажа. Эти ошибки можно объяснить тем, что лидару сложно фиксировать наклон и мгновенные изменения направления. В ровных городских условиях точность позиционирования снижается меньше. Таким образом, предлагаемая система SLAM обеспечивает точное позиционирование в крупномасштабных городских условиях.
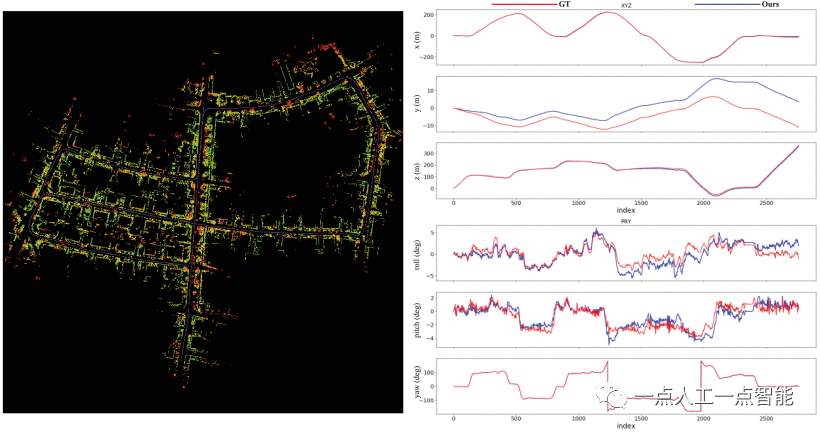
Траектория аппарата изогнута по схеме KITTI 05 длиной 2223 м. Транспортные средства проезжают через один и тот же перекресток с разных направлений, что затрудняет обнаружение петель. Благодаря введению дескрипторов, инвариантных к вращению, сканирование информации «до» и «после» может эффективно обнаруживать циклы в приведенных выше сценариях. Как показано на рисунке 10, предлагаемая система может построить трехмерную карту облака точек в сцене KITTI 05, которая в основном соответствует реальной среде. Точность позиционирования по направлениям x, y и рысканию близка к истинной. Как показано на рисунке 11, эпизод 07 — это еще одна городская сцена, отличная от эпизода 05. Транспортное средство совершает круг по городу и возвращается в исходную точку в последовательности 07. В этом случае предлагаемая система точно находит и строит трехмерные карты облаков точек с малым дрейфом. Результаты испытаний показывают, что система может точно позиционировать и отображать карту в трех различных городских сценариях KITTI.
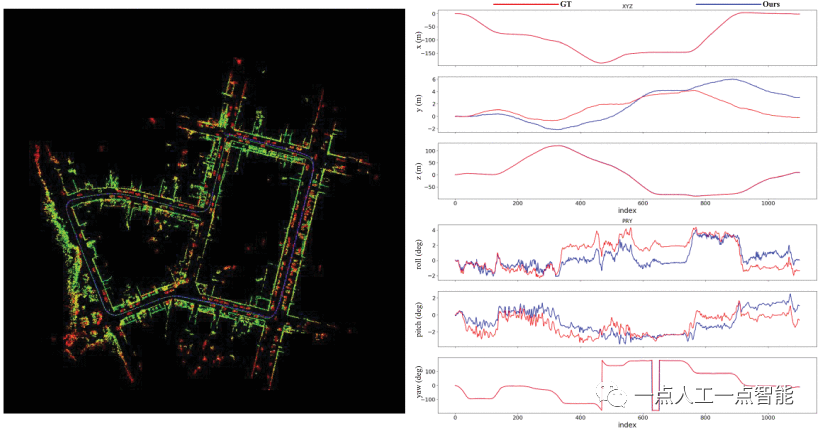
Проверьте осуществимость алгоритмов извлечения функций лидара с различным разрешением. Предложенный алгоритм был протестирован на наборе данных MVSECD [16] MVSECD, где горизонтальное и вертикальное разрешение LiDAR отличается от разрешения KITTI. Как показано на рисунке 12, синяя сплошная линия — это траектория нашего алгоритма, а красная линия — это основная истина. Наша система обеспечивает превосходную точность позиционирования в различных городских условиях. В дни 1 и 2 траектории, полученные с помощью предлагаемой системы, близки к истине, что подтверждает эффективность метода извлечения характерных точек с использованием информации о глубине без использования разрешения лидара, а также надежность предлагаемой системы SLAM для приложений в сложных городских условиях. среды.
5.3 Анализ, требующий много времени
Производительность предлагаемой системы SLAM в режиме реального времени была протестирована на последовательности 00 KITTI. Время работы системы сравнивалось с ALOAM и FLOAM. Эксперименты проводились на платформе ПК с процессором Intel Core i7-10700 2,90 ГГц, а тестовая среда была основана на ROS Melodic и Ubuntu 18.04 LTS. На входе было проверено время выполнения сегментации земли, выделения признаков и оценки положения на расстоянии соответственно. На серверной стороне обнаружение циклов и оптимизация графа поз объединены в один модуль для проверки времени. Как показано в таблице 2, среднее время работы модуля сегментации дорожного покрытия, модуля извлечения признаков и модуля оценки положения одометра составляет 26, 29 и 21 мс соответственно. Весь интерфейс занимает в среднем 76 мс. По сравнению с ALOAM и FLOAM предлагаемый алгоритм извлечения признаков с использованием метода адаптивного выбора извлекает меньше точек. Таким образом, оценка позы в нашей системе занимает меньше времени. Время работы переднего одометра в нашей системе на 23 мс быстрее, чем у ALOAM. Фронтенд и FLOAM в предлагаемой системе занимают практически одинаковое время. Поскольку количество облаков точек увеличивается в процессе рисования, время рисования FLOAM и ALOAM также увеличивается. Однако в нашей системе меньше характерных точек и, следовательно, лучшее картографирование в реальном времени. Для серверной части цикл возникает после того, как транспортное средство проработало некоторое время. Сопоставление оптимизируется только при возникновении циклов. Мы используем более низкую частоту 2 Гц для обнаружения петель. Весь бэкэнд занимает в среднем 290 миллисекунд.
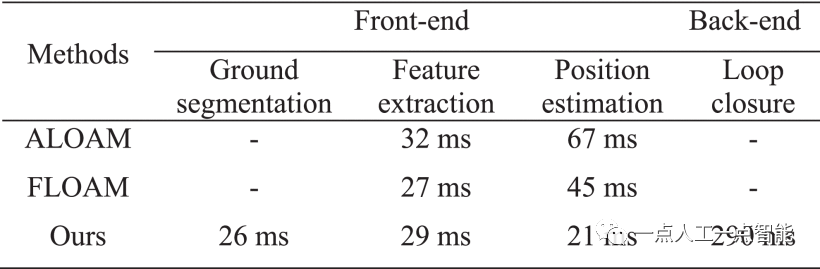
Бэкэнд занимает больше времени, чем фронтенд, из-за необходимости оптимизировать и обновлять глобальную карту и позу. Следует отметить, что оптимизация и обновление глобальной карты выполняются только при возникновении цикла, а не в каждом кадре. Поэтому его влияние на производительность системы в реальном времени незначительно. Результаты испытаний показывают, что предлагаемая система SLAM демонстрирует превосходные характеристики в реальном времени во всех вышеперечисленных тестах. Система может быть применена к автономным транспортным средствам с устройствами с ограниченными ресурсами.
06 Заключение
В этой статье предлагается легкая 3D-лидарная система SLAM в реальном времени для решения проблем локализации и картографирования автономных транспортных средств в больших и сложных городских условиях. Система включает в себя сегментацию поверхности, кодирование глубины, извлечение признаков на основе улучшенного PCA и обнаружение петель.
Кодирование неупорядоченных облаков точек, не являющихся наземными, на основе информации о глубине. Закодированное облако точек сохраняет трехмерную информацию без проецирования на двухмерную плоскость. Этот метод кодирования можно применять к лидарам с различным разрешением. Улучшенный метод адаптивного выбора точек соседства в PCA повышает скорость извлечения признаков. Выбирая различное количество характерных точек в зависимости от расстояния, можно извлечь равномерно распределенные точки с шестью степенями свободы, чтобы повысить точность позиционирования одометра.
В наборе данных KITTI средняя ошибка перевода одометрии составляет всего 1,17%, а средняя ошибка вращения — всего 0,052 (°/1м). Из-за небольшого количества точек, извлеченных методом адаптивного извлечения признаков, оценка позы при одометрии занимает всего 21 мс. Весь интерфейс занимает 76 мс, обеспечивая производительность в реальном времени. Контекст сканирования и ICP используются для обнаружения шлейфа, чтобы устранить накопленные ошибки сопоставления. Оптимизируйте глобальное картографирование, используя методы оптимизации на основе графов. Чтобы продемонстрировать надежность предлагаемой системы в различных городских сценариях, ее производительность оценивается на основе наборов данных KITTI и MVSECD. В различных сценариях использования двух вышеупомянутых наборов данных точность позиционирования системы может быть близка к истинной.
- Все в одной статье | Комплексный обзор развития прогнозирования траекторий за последние два десятилетия!
- Рекомендация к книге - "Введение в автономных мобильных роботов"
- PythonRobotics | Автономная навигация робота на базе Python
- IROS2022 | Лазерная обработка облаков точек в заснеженных условиях
- Глобальное планирование пути | Принцип и реализация алгоритма RRT
- 20 000 слов | Обзор визуального исследования SLAM и обсуждение будущих тенденций
- Принципы, текущее состояние и тенденции визуального обнаружения шлейфа SLAM мобильных роботов

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
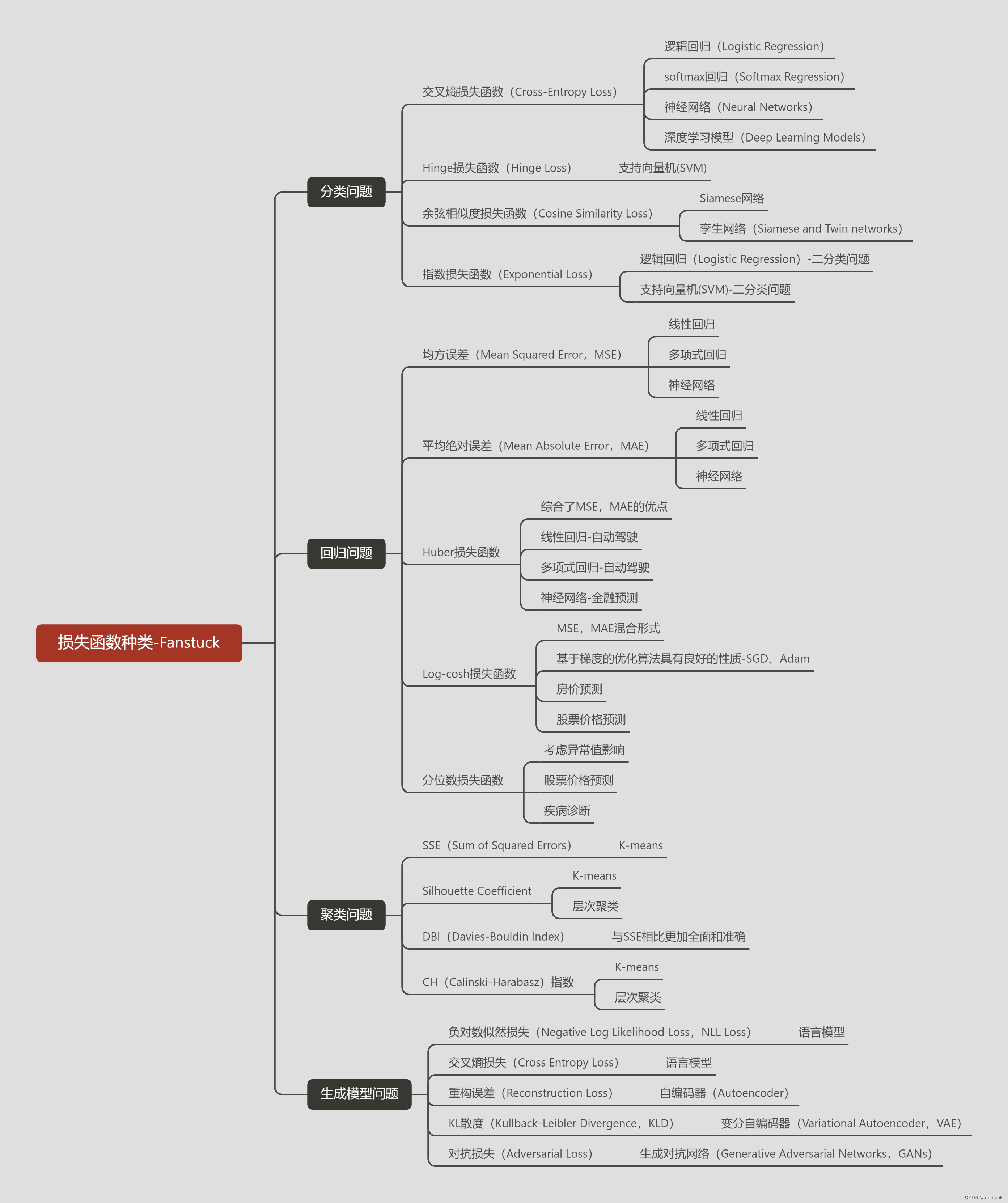
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
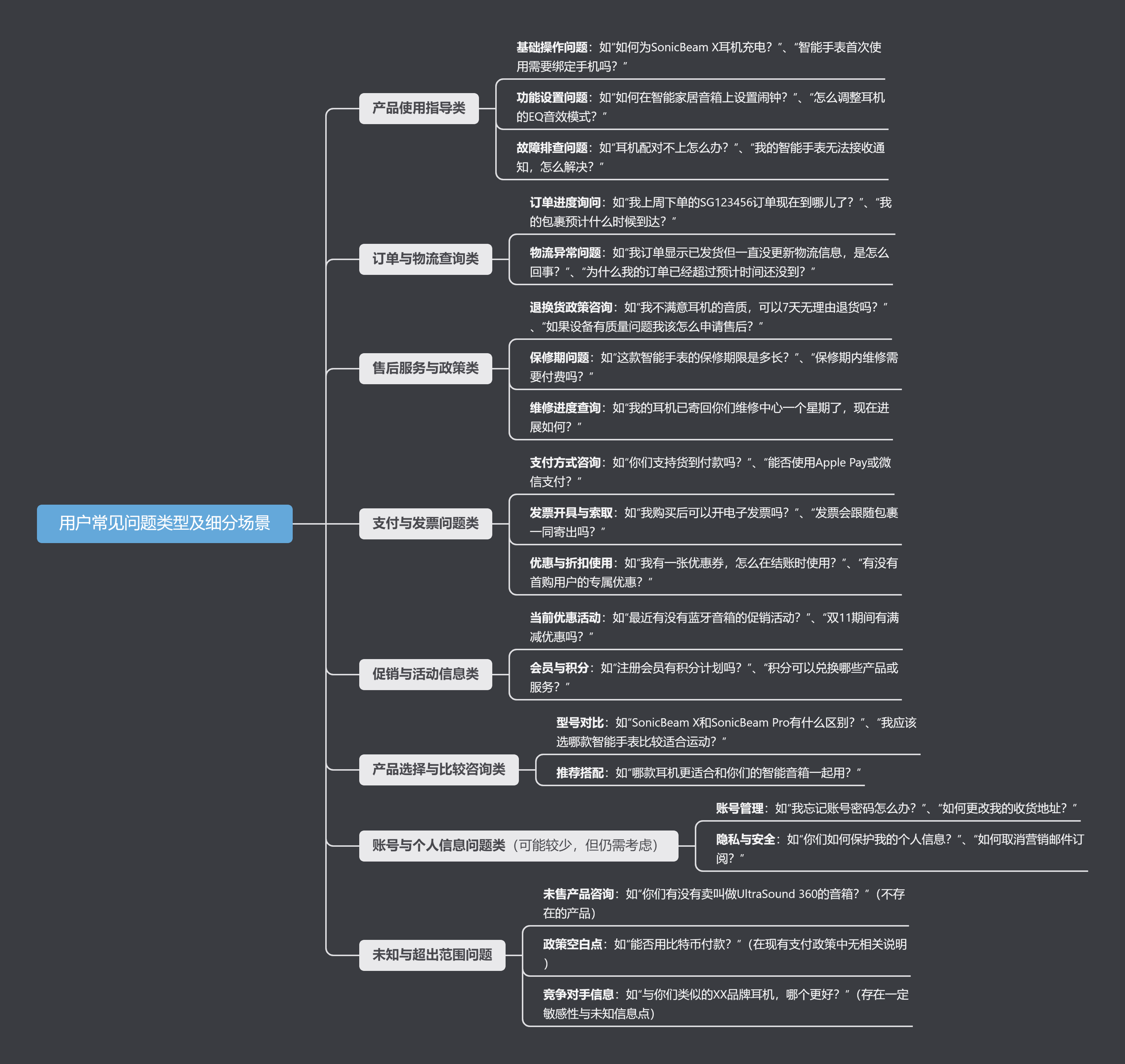
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.