Куайшоу | Оценка LTV посредством группирования
Название: Прогнозирование жизненной ценности клиентов с числом миллиардов пользователей: решение промышленного масштаба от Kuaishou Ссылка: https://arxiv.org/pdf/2208.13358.pdf. Конференция: CIKM 2022 Компания: Куайшоу
1 Введение
Эта статья представляет собой схему прогнозирования жизненного цикла пользователя (LTV), предложенную Куайшоу для использования в промышленных сценариях. Основные идеи состоят из трех частей: 1. Предложена монотонная сеть зависимости заказов (ODMN, монотонная сеть зависимости заказов) для прогнозирования взаимосвязи между LTV. Зависимости порядка модели для решения проблемы больших ошибок прогнозирования LTV в существующих моделях на большие промежутки времени. 2. Предложить мультираспределение с несколькими экспертами (MDME, Multi Distribution Multi); Эксперты) модуль, основанный на идее «разделяй и властвуй», разделяет общее распределение данных на подраспределения данных с несколькими сегментами для решения проблемы сложных данных и несбалансированного распределения в моделировании LTV. 3. Предложите относительный коэффициент Джини; коэффициент для количественной оценки дисбаланса возможностей распределения меток.
2 метода
2.1 Моделирование проблемы
Учитывая вектор функций пользователя x в фиксированном временном окне (например, 7 дней), спрогнозируйте ценность, которую он может принести платформе в следующие N дней.
, можно эмпирически сделать вывод, что чем дольше промежуток времени, тем выше ценность, которую он приносит. Прямо сейчас:
Многозадачная структура должна одновременно прогнозировать LTV в различных промежутках времени на основе входных данных x.
2.2 Общий слой emb и кодировка пользовательского представления

Как показано на рисунке, входной признак x представлен как низкоразмерный непрерывный вектор через общий слой внедрения. Среди них сначала будут дискретизированы непрерывные функции. Для некоторых непрерывных функций с распределением с длинным хвостом в этой статье используется равночастотная обработка. Наконец, каждый вектор представления функций напрямую объединяется в окончательное пользовательское представление.
В реальных сценариях LTV пользователя чувствителен к временным узлам, например, во время рекламной акции электронной коммерции, выходных или праздников и т. д. Поэтому ко входным данным будут добавлены периодичность, сезонность и другие характеристики. Кроме того, будь то маркетинг, реклама или другой бизнес, эффективность прогнозирования LTV пользователей на разных каналах также различна. Поэтому в эту статью также добавлена некоторая информация, связанная с каналом, чтобы улучшить способность модели прогнозировать LTV по размеру канала.
2.3 Многораспределенный многоэкспертный модуль (MDME)
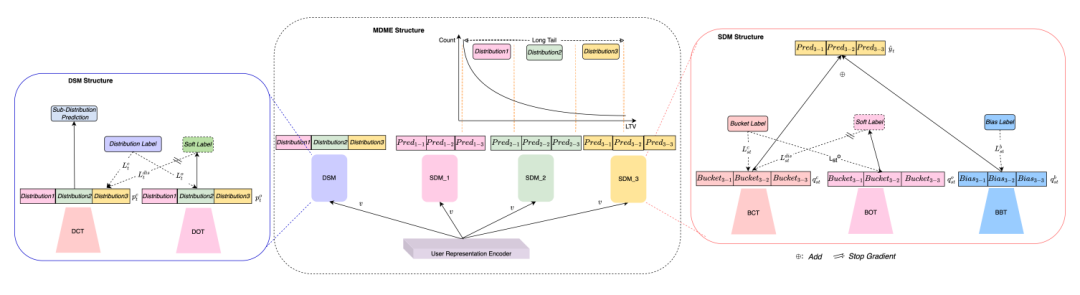
Из-за несбалансированного распределения выборки трудно хорошо изучить выборки в части с длинным хвостом. Упомянутое здесь распределение основано на значении LTV. Теоретически модели легче учиться на более сбалансированном распределении выборки, чем на несбалансированном распределении выборки. Вдохновленная этим, в данной статье делается попытка разбить всю выборку на несколько сегментов в соответствии с распределением LTV, чтобы можно было значительно смягчить дисбаланс распределения LTV в каждом сегменте.
На рисунке выше показана структура MDME. Весь сквозной процесс обучения состоит из трех частей: 1. Модуль сегментации распределения (DSM) реализует сегментацию LTV, то есть мультиклассификацию субраспределения. Набор выборок делится на несколько наборов подраспределений на основе значения LTV. Модулю необходимо изучить взаимосвязь между выборками и подраспределениями. Это типичная проблема мультиклассификации. На этом этапе определяется метка выборки. как количество субраспределений. 2. Модуль моделирования субраспределения (SDM, Модуль моделирования субраспределения) дополнительно делит каждое субраспределение на несколько сегментов в соответствии с фактическим значением LTV выборки в субраспределении и преобразует моделирование субраспределения в мультираспределение. -проблема классификации сегментов, так что ширину сегмента можно регулировать, чтобы размер выборки внутри сегмента оставался примерно одинаковым. Меткой образца на этом этапе является номер сегмента.
После двух этапов переопределения меток сложность моделирования всего распределения LTV была значительно снижена, а степень детализации моделирования была уменьшена для каждого сегмента. На данный момент распределение LTV выборок в каждом сегменте стало относительно сбалансированным. Третья часть — изучить отклонение данных в сегменте. В этой статье используется метод нормализации min-max для сжатия значения LTV выборки в сегменте до значения от 0 до 1, а также используется регрессия MSE для моделирования сжатого значения.
С точки зрения структуры модели, DSM состоит из башни классификации распределения (DCT) и башни порядкового распределения (DOT). SDM состоит из башни классификации по сегментам (BCT), башни порядковых номеров (BOT) и башни смещения по сегментам (BBT). Среди них DCT и BCT имеют схожие структуры, соответственно реализуя мультиклассификацию подраспределений и мультиклассификацию сегментов внутри подраспределений. Оценочная вероятность каждого подраспределения в DCT используется как вес сегментного полиномиального распределения внутри каждого подраспределения, тем самым получая нормализованное сегментное полиномиальное распределение всего LTV.
2.4 Нормализованное полиномиальное распределение и независимые единицы
Значения LTV в разные промежутки времени удовлетворяют упорядоченным отношениям, таким как
. Традиционные стратегии моделирования используют независимые модели для оценки определенной цели или просто изучают LTV для нескольких промежутков времени одновременно на основе многозадачного обучения. Однако упорядоченная зависимость между LTV разных временных интервалов не используется полностью. В этой статье считается, что моделирование этой упорядоченной зависимости может эффективно улучшить производительность модели с помощью многослойного перцептрона с несколькими неотрицательными параметрами скрытого слоя (так называемая единица оппозиции (Моно). Unit), выходные слои задач прогнозирования LTV восходящего и нисходящего потока соединены последовательно, так что информация о распределении, выводимая предыдущей задачей, может быть связана монотонно и напрямую влиять на распределение выходных данных последующих задач. Причина, по которой Mono Unit подключен к выходному слою каждой сети задач, заключается в том, что чем ближе он к выходному слою, тем богаче информация, связанная с задачей, которую теоретически может получить скрытый уровень.
2.5 Детальная калибровка и совместная оптимизация многозадачного обучения
Для каждого модуля MDME потери, связанные с модулем DSM, включают потери перекрестной энтропии нескольких классов подраспределения.
,убыток упорядоченной регрессии субраспределения
, и перекрестная энтропийная потеря классификации дистилляции субраспределения
. Потери каждого модуля SDM состоят из многоклассовых потерь перекрестной энтропии.
, потери упорядоченной регрессии сегмента
, перекрёстная потеря энтропии при классификации ковшовой перегонки
и потери регрессии смещения сегмента
состав. Порядковая регрессионная потеря определяется следующим образом:
Следует отметить, что обучение модуля DSM требует использования всех выборок, а для модуля SDM для выделения обучающих выборок используются только выборки, принадлежащие подраспределениям или сегментам. Независимый модуль Mono Unit фиксирует тенденцию изменения полиномиального распределения сегментов выходных данных вышестоящей задачи, что, в свою очередь, влияет на выходное распределение нижестоящей задачи, тем самым достигая монотонных ограничений в виде крупнозернистой формы. Чтобы дополнительно смоделировать отношения монотонных ограничений между восходящими и нисходящими задачами, в этой статье выполняется детальная калибровка предполагаемого значения LTV каждой задачи. В частности, если краткосрочный LTV, оцененный восходящей задачей, больше, чем долгосрочный LTV, оцененный соседней нисходящей задачей, вводится термин штрафных потерь:
Подводя итог, функция потерь ODMN определяется следующим образом:
Контроль силы мелкозернистых калибровочных потерь, зависящих от порядка,
и
Определим потери для каждой дистилляционной фракции:
2.6 Взаимный коэффициент Джини

В этой статье также предлагается новый индекс оценки, называемый Взаимный коэффициент Джини (Взаимный коэффициент Джини). Джини), количественная мера разницы между кривыми, основанными на кривой Лоренца. Как показано на рисунке выше, зеленая кривая — это кривая Лоренца реальной метки, красная кривая — оценка, а взаимный Джини определяется как площадь A между зеленой кривой и красной кривой. Чем меньше взаимный коэффициент Джини, тем лучше модель соответствует истинному распределению дисбаланса. Взаимный коэффициент Джини рассчитывается следующим образом:
и
представляют собой кривые Лоренца истинной метки и оценочного значения соответственно.,Определение взаимного Джини помогает измерить общую точность распределения LTV.,Вместо точечной оценки потери прогноза LTV
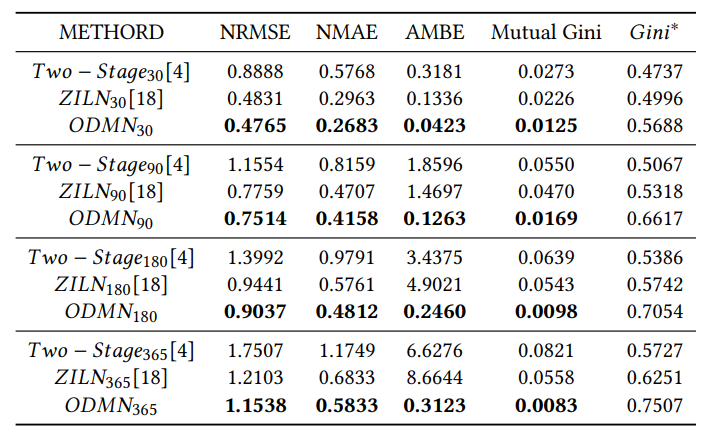
3 эффекта
следующие 30 дней、90 дней、Сравнение расчетного значения LTV на 180 и 365 дней.
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
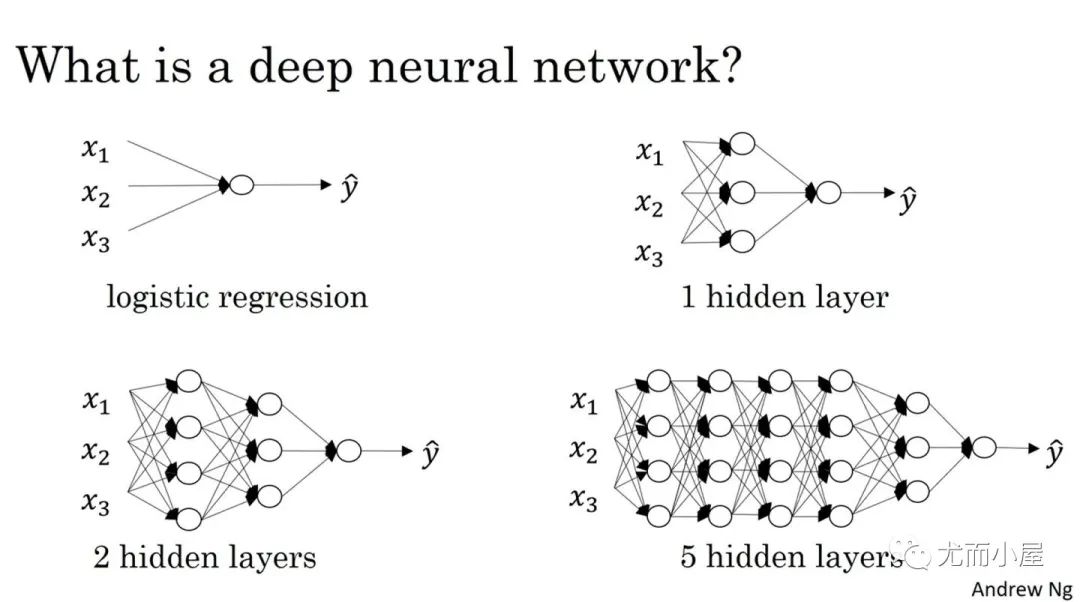
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


