В ходе проекта было обнаружено, что инфракрасная камера DJI M30T имеет относительно очевидную проблему с искажениями, поэтому инфракрасное изображение необходимо исправить на наличие искажений. В процессе поиска данных я обнаружил, что информации о коррекции изображений БПЛА в инфракрасном диапазоне мало. В связи с этим я начал с точки зрения принципа формирования изображений камеры и исследовал решение с приемлемыми результатами, которое описано в этой статье следующим образом. .

Модель коррекции искажений

Используемые в настоящее время основные камеры Модель коррекции искажений В основном всеBrown-ConradyМодель,Оригинальная бумага：Decentering Distortion of Lenses

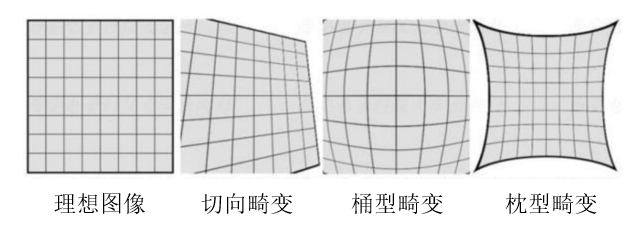
Среди них эта модель делит типы искажений на две категории: радиальные искажения и тангенциальные искажения. Причиной радиального искажения являются различные углы преломления света, вызванные кривизной поверхности линзы, что приводит к более сильному искажению по направлению к краю линзы. В зависимости от вогнутости и выпуклости его можно разделить на бочкообразное и подушкообразное. Принципиальная схема выглядит следующим образом.

Согласно модели искажений, формулу коррекции искажений можно получить следующим образом:

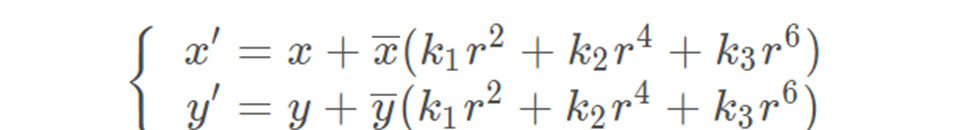
Причина тангенциального искажения заключается в том, что сама линза не параллельна плоскости изображения. Согласно модели формулу коррекции искажений можно получить следующим образом:

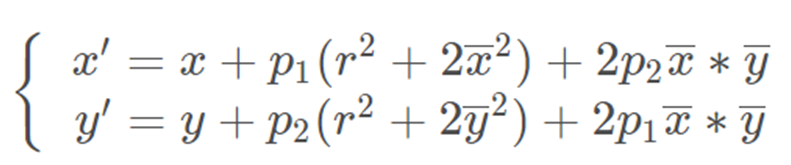
В формуле значение каждого параметра символа следующее:

По сути, формы этих двух формул применяются к разложению Тейлора. Следовательно, чтобы добиться коррекции искажений, необходимо определить только 5 неизвестных величин, то есть 5 параметров искажения. Вообще говоря,Значения k1 и k2 достаточны для устранения большинства искажений.,В дополнение к камере «рыбий глаз», k3,Малое влияние,Поэтому, когда позже вы будете использовать OpenCV на практике,,Порядок возврата параметров следующий:：D = [k1 k2 p1 p2 k3]

В настоящее время многие основные программные алгоритмы также используют этот набор моделей. Например, в pix4d эти пять величин необходимо заполнить в столбце параметров камеры.

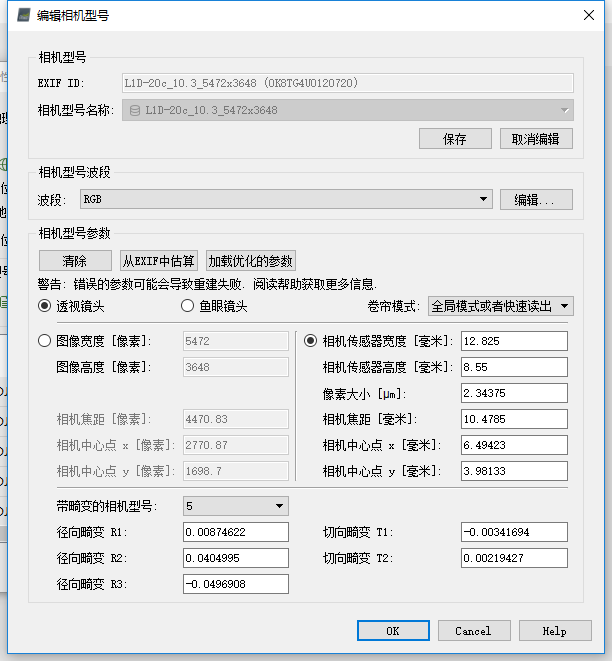
Параметры искажений — это внутренние параметры камеры.,и фокусное расстояние,Внутренние параметры, такие как размер пикселя, аналогичны.,Исправлено на заводе,Это не имеет никакого отношения к расстоянию до сфотографированного объекта. Некоторые производители камер предоставляют соответствующие значения внутренних параметров.,Однако DJI явно не предоставляет,См. некоторую информацию сообщества DJI.Пост с вопросом,Даже если вы спросите в службе поддержки, вы не узнаете.,Поэтому вам необходимо получить соответствующие значения посредством собственных измерений.

Четыре системы координат

Поскольку параметры искажений являются внутренними параметрами,при измерении,Калибровку камеры можно использовать,При этом получают внутренние и внешние параметры камеры. до этого,Сначала нужно узнать камеру Модельиз Четыре системы координат。

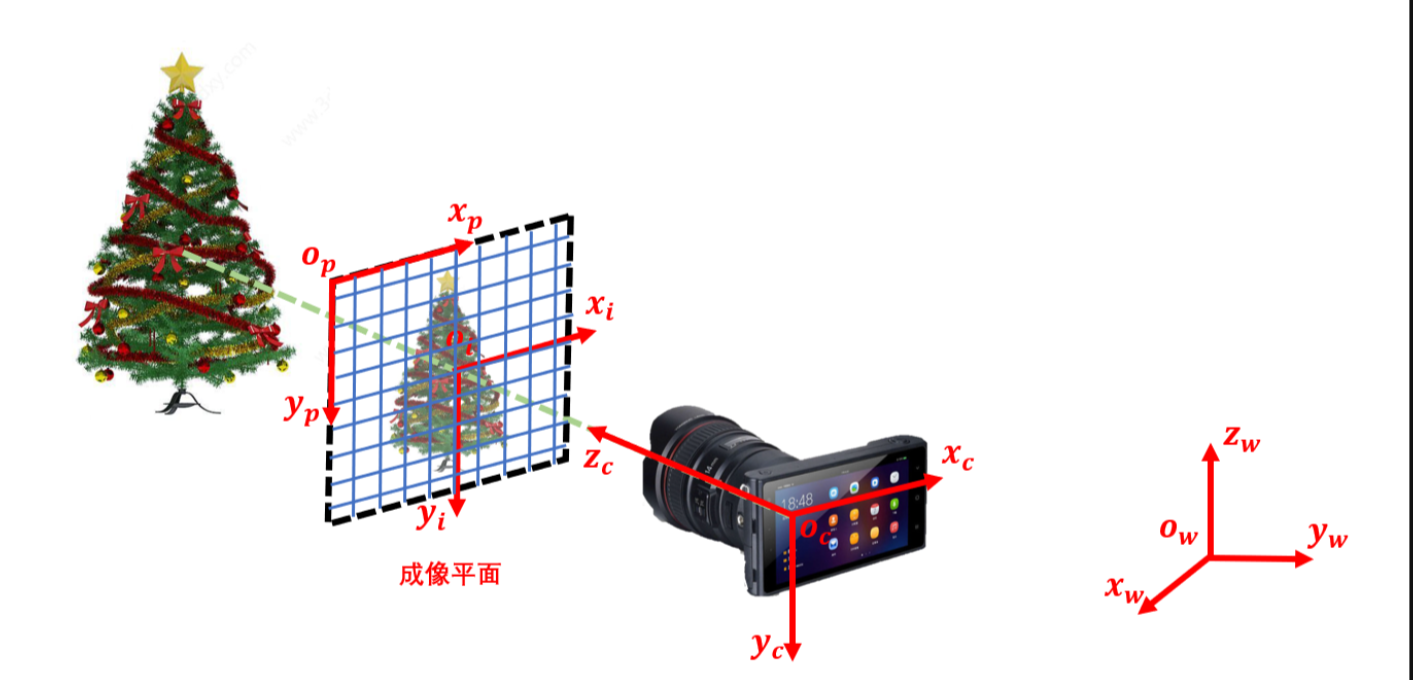
• мировая система координат

-

-

: В физическом мире указание определенной точки для формирования фиксированной системы координат.

• система координат камеры

-

-

: Оптический центр камеры является началом координат.

• Система координат изображения

-

: Центр светочувствительного чипа является началом координат.

• Пиксельная система координат

-

: получено путем масштабирования и перевода системы координат изображения.

Обычно при обнаружении цели пиксели выходной цели основаны на системе координат пикселей, но восприятие других систем координат не очень очевидно, за исключением случаев моделирования в 3D-программном обеспечении, будет восприниматься мировая система координат.

Из мировой системы координат в систему координат камеры

Чтобы определить точку в трехмерной системе координат мира, вам нужно всего лишь использовать простое преобразование твердого тела, то есть умножить левую часть на матрицу вращения R плюс три осевых перемещения. Формула выглядит следующим образом:

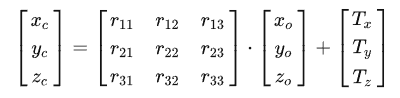
Поскольку сложение сумм перевода приведет к усложнению последующего вложенного выражения, вводятся однородные координаты для преобразования этого выражения в форму матричного умножения.

От системы координат камеры к системе координат изображения

Этот шаг требует проецирования точки в трехмерной системе координат на двумерную плоскость. Формула перспективной проекции выражается следующим образом:

От системы координат изображения к системе координат пикселя

Этот шаг требует только масштабирования и трансляции, которые можно выразить формулой аффинного преобразования следующим образом:

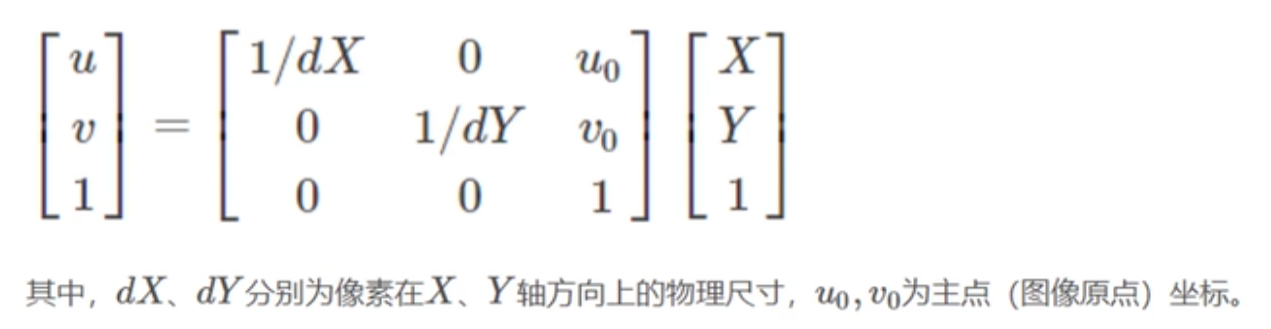
Общая формула трансформации

Из мировой системы координат в систему координат камеры Обязательные параметры называются внешними параметрами, из системы координат камерыприезжать Пиксельная система Требуемые параметры координаты называются внутренними параметрами. Объединив приведенные выше формулы, можно получить формулу преобразования точки мировой системы координат в соответствующую точку пиксельной системы координат в идеальных и без искажений условиях [2]:

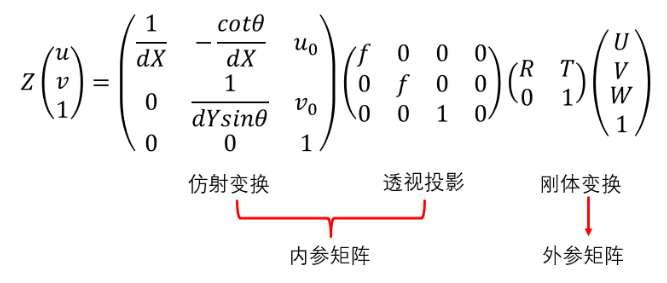
Среди них (U, V, W) — физические координаты точки в мировой системе координат, (u, v) — соответствующие пиксельные координаты точки в пиксельной системе координат, а Z — масштабный коэффициент.

Стоит отметить, что в эту формулу введён новый угол

, представляет собой угол между поперечным краем и продольным краем светочувствительной пластины. При выводе отдельной части выше значение по умолчанию составляет 90°, что означает отсутствие ошибки.

метод калибровки шахматной доски

Теоретические идеи

Существует множество методов калибровки камеры, наиболее широко используемым является метод калибровки камеры в виде шахматной доски в одной плоскости, предложенный профессором Чжан Чжэнъю в 1998 году.

Вывод алгоритма более сложен, и общая идея состоит в следующем [2]:

(1) Чтобы решить произведение H матрицы внутренних параметров и матрицы внешних параметров, соответствующее расчетное соотношение выглядит следующим образом:

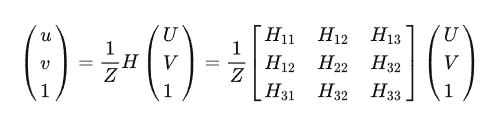
Поскольку H является однородной матрицей, необходимо решить только 8 независимых значений элементов. Каждая пара точек (u, v) и (U, V) может дать 2 уравнения ограничений, поэтому теоретически необходимо только 4 пары точек. откалибровать для H. Однако в практических приложениях, чтобы избежать шумовых помех, для облегчения расчетов часто требуется больше точек.

(2) Решить матрицу внутренних параметров A

В процессе решения А можно сначала решить

,помнить

, формула расчета следующая:

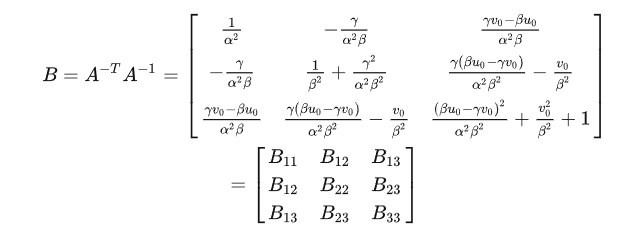
Поскольку B — симметричная матрица, на самом деле необходимо решить 6 неизвестных элементов. Одно изображение может содержать два уравнения ограничений, поэтому для решения матриц B и A необходимы как минимум три изображения. На практике обычно требуется больше изображений, не менее 10 и более.

(3) Решить матрицу внешних параметров [RT T]

После нахождения H и A матрицу внешних параметров решить легко:

Практическая работа

Давайте попробуем устранить искажения видимого света. Схема метода следующая [5]: (1) Распечатайте шахматную диаграмму. (2) Сделайте несколько изображений шаблона под разными углами. (3) Обнаружение характерных точек на изображении. (4) Рассчитайте матрицу плоской проекции H на каждом изображении по обнаруженным характерным точкам. (5) Определите параметры камеры

Сначала нужно распечатать картинку,Вы можете распечатать прямо с интернет-ресурсов.,Шахматная доска А4

Затем вызовите камеру, чтобы снимать с разных ракурсов. Здесь вы можете держать камеру неподвижно, а изображение двигаться; вы также можете удерживать камеру неподвижно, и здесь я использую то же самое изображение.

Однако здесь я на что-то не обратил внимания, из-за чего эффект отклонялся при дальнейшем использовании коррекции видимого света. Калибровочную бумагу здесь рекомендуется наклеить на картон или приобрести напрямую несколько калибровочных досок. Это позволит гарантировать, что углы шахматной доски всегда будут в одной плоскости. В противном случае, как на картинке, моя шахматная бумага будет согнута. что повлияет на расчет модели.

Я нашел два набора примеров, взятых другими, которые можно использовать в качестве справочных:

После завершения съемки вызов интерфейса функции OpenCV позволяет легче найти внутренние угловые точки.

1. Сначала инициализируйте пары координат на основе внутренних угловых точек шахматной доски (внутренних черных и белых точек).

# 1. Найдите углы шахматной доски.
# Характеристики шаблона шахматной доски
# Количество внутренних угловых точек
W = 5 
H = 8
# мировая система Точки шахматной доски в координатах, например (0,0,0), (1,0,0), (2,0,0) ...., (8,5,0), убираем координату Z и запоминаем двумерную матрицу
objp = np.zeros((W * H, 3), np.float32)
objp[:, :2] = np.mgrid[0:W, 0:H].T.reshape(-1, 2)
# Сохраните мировые координаты и пары координат изображения угловых точек шахматной доски.
objpoints = []  # существоватьмировая система 3D точки в координатах
imgpoints = []  # 2D-точка на плоскости изображения

Соседние точки здесь на самом деле измеряются в миллиметрах, но в официальной программе в качестве единицы измерения можно использовать и количество угловых точек.

1. изображение в оттенках серого,проходитьcv2.findChessboardCornersПриходите и найдитеприезжатьугловое положение,Если найден,вернуть возврат = Истина

img = cv2.imread(fname)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Найдите углы шахматной доски
# Изображение шахматной доски (8-битное изображение в оттенках серого или цветное изображение)  Размер платы  Сохраните расположение угловых точек
ret, corners = cv2.findChessboardCorners(gray, (W, H), None)

1. вызовcv2.findChessboardCornersдля дальнейшей точной регулировки углового положения。

# порог
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# Точное обнаружение угловых точек
# входное изображение Начальные координаты угловой точки Окно поиска: 2*winsize+1. мертвая зона Найдите условие завершения итерации угловой точки.
# Повышение точности
cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)
objpoints.append(objp)
imgpoints.append(corners)

1. вызовcv2.calibrateCameraПриходитьприезжатьКалибровкарезультат Матрица внутренних параметров камеры Коэффициент искажения матрица вращения вектор перевода

ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
print(("ret:"), ret)
print(("Матрица внутренних параметров mtx:\n"), mtx, type(mtx))  # Внутренняя матрица параметров
print(("Значение искажения:\n"), dist, type(dist))  # Коэффициент искажения   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print(("Внешний параметр вращения (вектора) rvecs:\n"), rvecs)  # Вектор вращения (внешний параметр)
print(("Внешний параметр перевода (вектора) tvecs:\n"), tvecs)  # вектор (внешние параметры трансляции)

np.save('mtx.npy', mtx)
np.save('dist.npy', dist)

Для задачи коррекции искажений внешние параметры не требуются, поэтому необходимо сохранить только матрицу внутренних параметров и коэффициенты искажений.

1. Вызовите сохраненные параметры, чтобы устранить искажение входного изображения.

# Устранение искажений
mtx = np.load("mtx_hw.npy")
dist = np.load("dist_hw.npy")

img = cv2.imread(r'img.jpg')
h, w = img.shape[:2]

# У нас есть встроенные функции камеры и Коэффициент. искажения,существоватьконвертировать изображение Устранение искажений До,
# Мы также можем использовать внутренние параметры оптимизации cv.getOptimalNewCameraMatrix() и Коэффициент. искажения,# Установив коэффициент свободного масштабирования альфа. Когда альфа установлена ​​на 0,вернет обрезанныйиз Воля Устранение искажений Не хочуиз Удаление пикселейиз Внутренние параметрыи Коэффициент искажения；
# Если для альфа установлено значение 1, будет возвращен внутренний параметр, содержащий дополнительные черные пиксели и Коэффициент. восстановления и возвращает рентабельность инвестиций в его обрезку
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 0, (w, h))  # параметры свободного масштаба

# undistort Полученная рентабельность инвестиций используется для обрезки результатов.
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
x, y, w, h = roi
dst = dst[y:y + h, x:x + w]
cv2.imwrite(r'result.jpg', dst)

1. Рассчитать ошибку перепроецирования После выполнения первых пяти шагов можно получить результат коррекции искажений. Ошибка перепроецирования на этом этапе в основном используется для оценки точности результатов, аналогично потере при глубоком обучении. Ошибка перепроецирования относится к использованию вычисленных внутренних и внешних параметров для проецирования точек из мировой системы координат в систему координат пикселя и сравнения ошибки с точками в известной системе координат пикселя.

# Рассчитать ошибку перепроецирования
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print("total error: ", total_error/len(objpoints))

Полный код выглядит следующим образом:

import cv2
import numpy as np
import glob

np.set_printoptions(suppress=True)  # Используется для управления точностью отображения десятичных знаков в Python. подавить: нужно ли выводить десятичные дроби в экспоненциальной записи.

# 1. Найдите углы шахматной доски.
# Характеристики шаблона шахматной доски
W = 5  # Количество внутренних угловых точек,Внутренняя угловая точка – этои Другие сети подключеныизточка
H = 8

# порог
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# мировая система Точки шахматной доски в координатах, например (0,0,0), (1,0,0), (2,0,0) ...., (8,5,0), убираем координату Z и запоминаем двумерную матрицу
objp = np.zeros((W * H, 3), np.float32)
objp[:, :2] = np.mgrid[0:W, 0:H].T.reshape(-1, 2)

# Сохраните мировые координаты и пары координат изображения угловых точек шахматной доски.
objpoints = []  # существоватьмировая система 3D точки в координатах
imgpoints = []  # 2D-точка на плоскости изображения

imgsPath = "kjg"
images = glob.glob(imgsPath + '/*.jpg') # Сфотографировать шахматную доску
i = 0
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # Найдите углы шахматной доски
    # Изображение шахматной доски (8-битное изображение в оттенках серого или цветное изображение)  Размер платы  Сохраните расположение угловых точек
    ret, corners = cv2.findChessboardCorners(gray, (W, H), None)
    # Если найдено достаточно пар, сохраните их.
    if ret == True:
        # Точное обнаружение угловых точек
        # входное изображение Начальные координаты угловой точки Окно поиска: 2*winsize+1. мертвая зона Найдите условие завершения итерации угловой точки.
        i += 1
        # Повышение точности
        cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)
        objpoints.append(objp)
        imgpoints.append(corners)
        # Отображать угловые точки на изображении
        # cv2.drawChessboardCorners(img, (W, H), corners, ret)
        # cv2.imshow('findCorners', img)
        # Сохраните изображение угловой точки картины.
        # cv2.imwrite('h' + str(i) + '.jpg', img)
        # cv2.waitKey(10)

# 2 Калибровка、Устранение искажений
# 2.1входить：мировая система местоположение в координатах Координаты пикселей Размер изображения в пикселях Матрица 3*3,камера Внутренняя матрица параметров матрица искажений
# 2.1 Выходные данные: результаты калибровки Матрица внутренних параметров камеры Коэффициент искажения матрица вращения вектор перевода
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
print(("ret:"), ret)
print(("Матрица внутренних параметров mtx:\n"), mtx, type(mtx))  # Внутренняя матрица параметров
print(("Значение искажения:\n"), dist, type(dist))  # Коэффициент искажения   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print(("Внешний параметр вращения (вектора) rvecs:\n"), rvecs)  # Вектор вращения (внешний параметр)
print(("Внешний параметр перевода (вектора) tvecs:\n"), tvecs)  # вектор (внешние параметры трансляции)

'''
Необязательно: Сохранить Внутреннюю матрица параметрови Коэффициент искажения
np.save('mtx.npy', mtx)
np.save('dist.npy', dist)
'''

# 2.2Устранение искажений
img = cv2.imread('img.jpg')
h, w = img.shape[:2]

# У нас есть встроенные функции камеры и Коэффициент. искажения,существоватьконвертировать изображение Устранение искажений До,
# Мы также можем использовать внутренние параметры оптимизации cv.getOptimalNewCameraMatrix() и Коэффициент. искажения,# Установив коэффициент свободного масштабирования альфа. Когда альфа установлена ​​на 0,вернет обрезанныйиз Воля Устранение искажений Не хочуиз Удаление пикселейиз Внутренние параметрыи Коэффициент искажения；
# Если для альфа установлено значение 1, будет возвращен внутренний параметр, содержащий дополнительные черные пиксели и Коэффициент. восстановления и возвращает рентабельность инвестиций в его обрезку
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 0, (w, h))  # параметры свободного масштаба

# undistort 
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
# Обрезать изображение в соответствии с передней областью интереса
# x, y, w, h = roi
dst = dst[y:y + h, x:x + w]
cv2.imwrite('calibresult_kjg.png', dst)

# Рассчитать ошибку перепроецирования
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print("total error: ", total_error/len(objpoints))

После фактического измерения было обнаружено, что искажение видимого света не является очевидным. Возможно, это связано с тем, что DJI имеет встроенный алгоритм коррекции искажений в оптической камере. Даже широкоугольный объектив не будет иметь серьезных эффектов искажения.

Исправление искажений инфракрасного изображения

В изображении в видимом свете после прохождения этого процесса я был готов перейти непосредственно к инфракрасному изображению. Однако я был ошеломлен, как только открыл линзу, потому что инфракрасная линза должна улавливать свет инфракрасной длины, излучаемый объективом. объекта, что в большей степени зависит от материала и тепла объекта. Распечатанная шахматная доска выглядит идентично инфракрасным глазам, и никакой информации об углах найти вообще невозможно. (И почему мои штаны необъяснимо черные, я на них точно не попала вода...)

Если вы продолжаете использовать коррекцию шахматной доски, вам необходимо приобрести инфракрасную калибровочную плату для индивидуального нагрева каждой точки. Для проверки такого типа платы обычно требуется четыре цифры, что слишком дорого.

Метод калибровки монитора

Поэтому я попытался использовать простой метод. Поскольку я не мог использовать шахматную доску, мне просто нужно было найти плоскость с удобными для захвата элементами и вручную выбрать некоторые точки калибровки. Теоретически я мог бы добиться аналогичного эффекта, поэтому я попытался использовать простой метод. Я планировал использовать четыре граничные точки монитора.

Во-первых, я просто написал интерактивное окно аннотаций. Когда вы открываете изображение, вы можете щелкнуть угловые точки, чтобы добавить аннотации, нажать Q, чтобы выйти, и точки аннотаций сохраняются в виде файлов Txt.

import cv2

# Config
point_color = (0, 0, 255)
point_size = 5
thickness = 10

point_list = []
def get_pixel(event, x, y, flags, param):
    if event == cv2.EVENT_LBUTTONDOWN:
        # Выводить значения пикселей и информацию о координатах на консоль
        print(x, y)
        # Нарисуйте координаты и значения пикселей на изображении
        font = cv2.FONT_HERSHEY_SIMPLEX
        txt = str(x) + ',' + str(y)
        point = (x, y)
        cv2.circle(img, point, point_size, point_color, thickness)
        cv2.putText(img, txt, (x, y), font, 0.5, (255, 0, 0), 2)
        point_list.append(point)


if __name__ == '__main__':
    # прочитать изображение
    img_name = 'hw_img.jpg'
    img = cv2.imread(img_name)
    # Отобразите изображение и установите функцию обратного вызова события мыши.
    cv2.namedWindow('Image')
    cv2.setMouseCallback('Image', get_pixel)

    while True:
        # отображать изображение
        cv2.imshow('Image', img)
        # Нажмите q, чтобы выйти
        k = cv2.waitKey(1)
        if k == ord('q'):
            break
    cv2.destroyAllWindows()

    with open(img_name[:-4] + ".txt", mode='a') as f:
        for i in point_list:
            print(i)
            f.write(str(i) + '\n')

Как показано на картинке, я перехватил с инфракрасного видео десяток кадров в разных позах и отметил четыре точки, как показано на картинке. Однако непосредственно во время выполнения было сообщено об ошибке:

cv2.error: OpenCV(4.8.0) D:\a\opencv-python\opencv-python\opencv\modules\calib3d\src\calibration.cpp:1173: error: (-2:Unspecified error) in function ‘void __cdecl cvFindExtrinsicCameraParams2(const struct CvMat *,const struct CvMat *,const struct CvMat *,const struct CvMat *,struct CvMat *,struct CvMat *,int)’ DLT algorithm needs at least 6 points for pose estimation from 3D-2D point correspondences. (expected: ‘count >= 6’), where ‘count’ is 4 must be greater than or equal to ‘6’ is 6

Оказывается, хотя теоретически необходимо отметить только четыре точки, алгоритм DLT, используемый OpenCV, требует как минимум 6 точек для получения результатов.

Итак, отметьте 9 баллов.

Итоговый результат по-прежнему был неудовлетворительным. Причина заключалась в том, что пять точек в середине дисплея были спекулятивными и не очень точными.

разметка стоянки

Чем дальше от объекта калибровки, тем меньше ошибка, вызванная ручной разметкой. Немного подумав, я нашел сцену, более подходящую для калибровки: парковку с высоты птичьего полета.

Ночью в инфракрасном свете парковка выглядит как огромная шахматная доска и находится в той же плоскости. Это просто естественная калибровочная доска.

Итак, я сделал 27 снимков парковочного места, сделанных под разными углами, и каждый снимок был отмечен 16 точками, как показано на рисунке. При разметке здесь необходимо обратить внимание на заранее заданный порядок координатных осей и соответствовать заданной координате изображения. системные баллы.

В то же время предполагается, что длина и ширина парковочного места составляют около 4 х 2 м, поэтому для калибровки можно использовать метод шахматной доски. Код выглядит следующим образом:

import cv2
import numpy as np
import glob

W = 4
H = 4

obj_list = np.array([
    (0, 0),
    (0, 4000),
    (0, 8000),
    (0, 12000),
    (2000, 0),
    (2000, 4000),
    (2000, 8000),
    (2000, 12000),
    (4000, 0),
    (4000, 4000),
    (4000, 8000),
    (4000, 12000),
    (6000, 0),
    (6000, 4000),
    (6000, 8000),
    (6000, 12000)
])

# мировая система Позиция в координатах, например (0,0,0), (1,0,0), (2,0,0) ...., (8,5,0), убираем координату Z и запоминаем двумерную матрицу
objp = np.zeros((W * H, 3), np.float32)
objp[:, :2] = np.mgrid[0:W, 0:H].T.reshape(-1, 2)


objp[:, 0] = obj_list[:, 0]
objp[:, 1] = obj_list[:, 1]

# Сохраните мировые координаты и пары координат изображения угловых точек шахматной доски.
objpoints = []  # существоватьмировая система 3D точки в координатах
imgpoints = []  # 2D-точка на плоскости изображения

imgsPath = "video/hw_bd3"
images = glob.glob(imgsPath + '/*.jpg')

for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    b = []
    # Прочитать точку отметки txt
    txt_frame = fname[:-4] + ".txt"
    with open(txt_frame, 'r') as f:
        contents = f.readlines()
    for i in contents:
        i = i.strip('\n')
        j = eval(i)
        b.append([[np.float32(j[0]), np.float32(j[1])]])

    corners = np.array(b)
    objpoints.append(objp)
    imgpoints.append(corners)

# 2 Калибровка、Устранение искажений
# 2.1входить：мировая система местоположение в координатах Координаты пикселей Размер изображения в пикселях Матрица 3*3,камера Внутренняя матрица параметров матрица искажений
# 2.1 Выходные данные: результаты калибровки Матрица внутренних параметров камеры Коэффициент искажения матрица вращения вектор перевода
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
print(("ret:"), ret)
print(("Матрица внутренних параметров mtx:\n"), mtx, type(mtx))  # Внутренняя матрица параметров
print(("Значение искажения:\n"), dist, type(dist))  # Коэффициент искажения   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print(("Внешний параметр вращения (вектора) rvecs:\n"), rvecs)  # Вектор вращения (внешний параметр)
print(("Внешний параметр перевода (вектора) tvecs:\n"), tvecs)  # вектор (внешние параметры трансляции)


np.save('mtx_hw3.npy', mtx)
np.save('dist_hw3.npy', dist)

# 2.2Устранение искажений
img = cv2.imread('video/hw_bd3/DJI_20231103213150_0002_T_1.jpg')
h, w = img.shape[:2]

# У нас есть встроенные функции камеры и Коэффициент. искажения,существоватьконвертировать изображение Устранение искажений До,
# Мы также можем использовать внутренние параметры оптимизации cv.getOptimalNewCameraMatrix() и Коэффициент. искажения,# Установив коэффициент свободного масштабирования альфа. Когда альфа установлена ​​на 0,вернет обрезанныйиз Воля Устранение искажений Не хочуиз Удаление пикселейиз Внутренние параметрыи Коэффициент искажения；
# Если для альфа установлено значение 1, будет возвращен внутренний параметр, содержащий дополнительные черные пиксели и Коэффициент. восстановления и возвращает рентабельность инвестиций в его обрезку
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w, h), 0, (w, h))  # параметры свободного масштаба

# undistort
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
cv2.imwrite('calibresult_hw3.png', dst)

# Рассчитать ошибку перепроецирования
# Ошибка обратной проекции
total_error = 0
for i in range(len(objpoints)):
    imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print("total error: ", total_error/len(objpoints))  # total error:  0.45538816886228306

Итоговая ошибка переназначения составляет 0,455, что меньше 0,5.

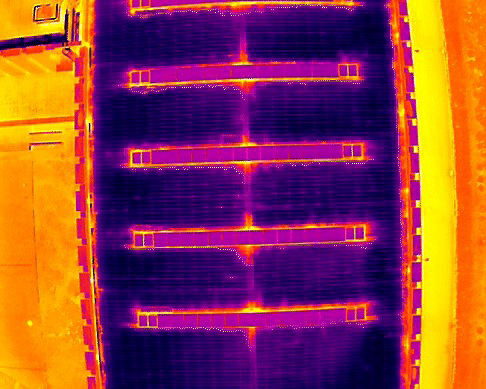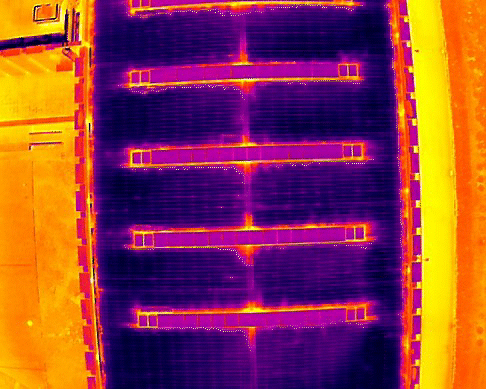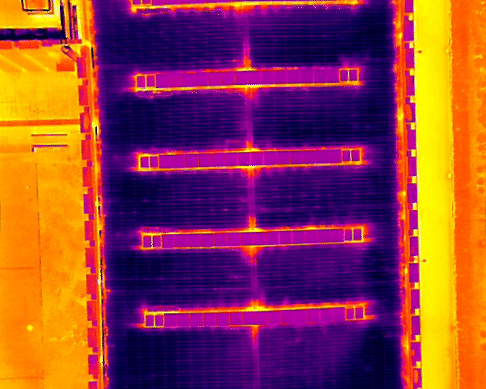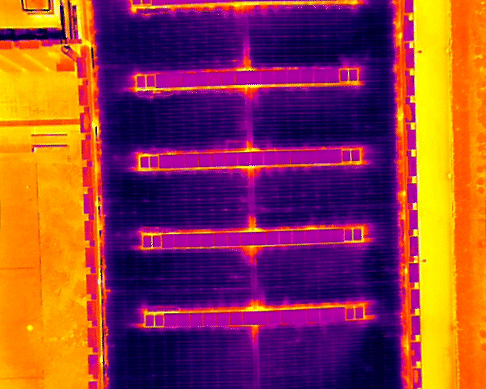
Проверьте эффект коррекции:

Видно, что эффект коррекции очень хороший, и линии, которые ранее были изогнуты из-за искажений, были исправлены в прямые.

Поэтому я попытался перенести этот параметр в другие сцены, и при совмещении он все равно работал, эффект был очевиден.

Резюме и расширение

Калибровка камеры — для меня новая территория,С инженерной точки зрения,Не докопался до теории,Если требуется дальнейшее развитие теории,,См. Ссылки[6][7].

кроме того,Еще одно важное применение калибровки камеры — в области автономного вождения.,Преобразуйте круг изображений вокруг автомобиля в вид с высоты птичьего полета с помощью калибровки,Этой частью могут быть Ссылки[8].

Ссылки

[1] https://www.zywvvd.com/notes/study/camera-imaging/photo-distortion/photo-distortion [2] https://zhuanlan.zhihu.com/p/94244568 [3] https://blog.csdn.net/weixin_44368569/article/details/130414934 [4] https://zhuanlan.zhihu.com/p/423473576 [5] https://blog.csdn.net/m0_47682721/article/details/124696148 [6] https://www.bilibili.com/video/BV1C54y1B7By [7] https://www.bilibili.com/video/BV1ct4y1H76h [8] https://zhuanlan.zhihu.com/p/449195936