Команда Ян Юэдуна из Университета Сунь Ятсена предложила модель MUSE для прогнозирования взаимодействия белков и лекарств с помощью системы максимизации вариативного ожидания.
Понимание взаимодействия белков с белками, лекарствами и другими биомолекулами имеет решающее значение для расшифровки молекулярных механизмов, лежащих в основе биологических процессов, и разработки новых терапевтических стратегий.
Современные вычислительные методы в основном предсказывают взаимодействия на основе молекулярных сетей или структурной информации, не интегрируя их в единую многомасштабную структуру. Хотя существуют некоторые методы многоуровневого обучения, предназначенные для объединения многомасштабной информации, эти методы часто слишком полагаются на одну шкалу и недостаточно подходят для других шкал, что может быть связано с дисбалансом многомасштабного обучения.
24 мая 2024 года команда профессора Ян Юэдуна из Университета Сунь Ятсена опубликовала статью «Вариационная структура максимизации ожидания для сбалансированного многомасштабного изучения взаимодействия белков и лекарств» в Nature Communications.

Автор предлагает MUSE, многомасштабную структуру обучения представлению представления максимизации вариационного ожидания (EM) (MUiti-Scale EM, MUSE), которая может оптимизировать различные масштабы в попеременном процессе из нескольких итераций. Эта стратегия эффективно объединяет многомасштабную информацию между атомной структурой и масштабами молекулярной сети посредством взаимного контроля и итеративной оптимизации, показывая потенциал для распространения на другие масштабы для вычислительного открытия лекарств. Результаты экспериментов показывают, что MUSE превосходит существующие модели.
Как показано на рисунке 1, MUSE — это многомасштабный метод обучения, который сочетает в себе моделирование молекулярной структуры и обучение сети взаимодействия белков и лекарств с помощью структуры максимизации вариационного ожидания (EM). Структура EM оптимизирует два модуля: шаг ожидания (E-шаг) и шаг максимизации (M-шаг) в чередующемся процессе из нескольких итераций. На этапе E MUSE использует структурную информацию каждой биомолекулы для изучения эффективных структурных представлений для обучения известным взаимодействиям и расширенным образцам на этапе M. Он принимает пары белков и лекарств и их структурную информацию на атомном уровне в качестве входных данных и дополняет их на основе предсказанных на М-шаге взаимодействий. М-шаг принимает в качестве входных данных сеть взаимодействия на молекулярном уровне, структурные вложения и предсказанные взаимодействия Е-шага и выводит предсказанные взаимодействия. Эта итеративная оптимизация между E-шагом и M-шагом обеспечивает интерактивный сбор молекулярной структуры и сетевой информации с разной скоростью обучения в двух масштабах. Взаимный контроль гарантирует, что каждая масштабная модель обучается соответствующим образом и используется эффективная информация в разных масштабах. MUSE устраняет несбалансированные функции в многоуровневом обучении и эффективно интегрирует иерархическую дополнительную информацию в разных масштабах.
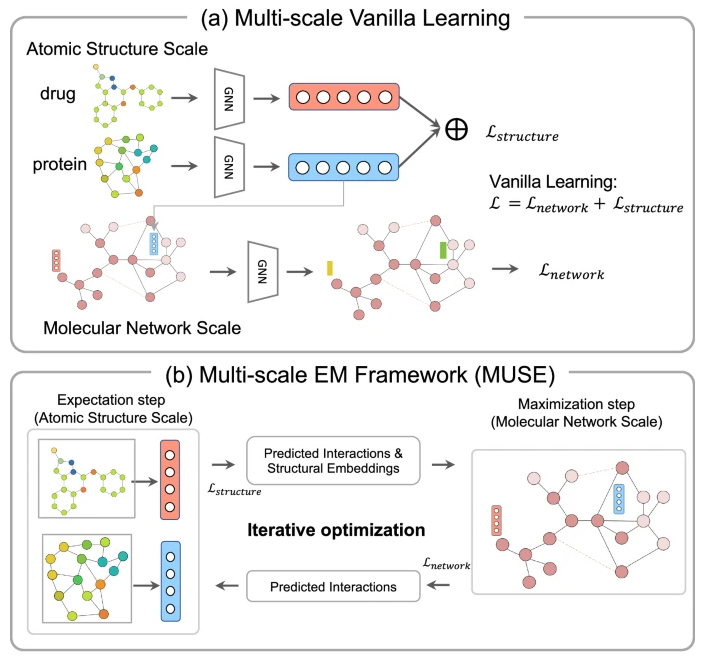
Рисунок 1. Структурная схема MUSE.
Ядром структуры максимизации вариационного ожидания (EM) является объединение масштаба атомной структуры и моделей масштаба молекулярной сети для выполнения обучения прогнозированию связей многомасштабных сетей в рамках вариационной структуры EM. Учитывая наблюдаемую вероятность переменной YLV, вероятность ненаблюдаемой переменной YLU и параметры модели θ, φ, структура EM пытается максимизировать логарифмическую функцию правдоподобия log pθ(YLU|YLV) наблюдаемых меток взаимодействия. Вычисление этой логарифмической вероятности является вычислительно сложным, поскольку требует интеграции всех комбинаций меток объектов, поэтому вместо этого алгоритм оптимизирует доказательную нижнюю границу (ELBO) функции логарифмического правдоподобия. Однако непосредственное получение оценки максимального правдоподобия с помощью алгоритма EM также является проблемой для ELBO. Поэтому авторы используют вариационную аппроксимацию алгоритма EM для оптимизации нижней границы путем итеративного чередования оптимизации альтернативного распределения q (называемого вариационным распределением) p (т. е. E-шага) и распределения p (т. е. М-шаг).
На вариационном этапе E цель состоит в том, чтобы зафиксировать pθ и обновить qφ, чтобы минимизировать расхождение KL, то есть сделать q и p как можно более похожими. На этапе M наша цель — обновить pθ, чтобы максимизировать функцию правдоподобия. , чтобы уменьшить вычислительную сложность pθ в EM-алгоритме, используется функция псевдоправдоподобия выборки окрестностей. Затем эту структуру можно применять для прогнозирования связей в многомасштабных сетях, создавая распределения p и q с помощью моделей масштаба атомной структуры qφ и масштаба молекулярной сети pθ соответственно.
Вариационный E-шаг направлен на обновление вариационного распределения qφ для аппроксимации истинного апостериорного распределения pθ(YLU|YLV), а цель состоит в том, чтобы минимизировать расхождение KL между апостериорным распределением и вариационным распределением. Чтобы смоделировать распределение каждого взаимодействия, qφ параметризуется масштабом атомной структуры GNNφ, чтобы предсказать метку взаимодействия YLU. Для этого используется структурный граф G биомолекул: в графе молекулы лекарственного средства узлами являются атомы, а ребрами — химические связи, в графе молекулы белка узлами являются группы аминокислотных остатков в белке, а края получены из трехмерных координат белка на атомном уровне, полученных из карты контактов белка, 10 Å было выбрано в качестве порогового расстояния для присутствия или отсутствия контакта между парой остатков для построения матрицы смежности. В качестве их узловых признаков можно использовать ряд физико-химических свойств атомов или аминокислотных остатков.
Теперь единственная трудность заключается в вычислении апостериорного распределения pθ, целью которого является предсказание распределения меток взаимодействий на основе особенностей окружающих узлов и информации о краях. Поскольку метки для ненаблюдаемых взаимодействий не указаны, мы предлагаем псевдометки, предсказанные моделью масштаба молекулярной сети GNNθ, для аннотирования ненаблюдаемых взаимодействий. Интуитивно этот процесс взаимодействия можно рассматривать как процесс дистилляции знаний, который оптимизирует модель GNNφ в масштабе атомной структуры, направляя ее для прогнозирования распределения меток на основе псевдовзаимодействий, предсказанных моделью молекулярной сети GNNθ, используя заданные взаимодействия меток для обучение.
Следовательно, на этапе M необходимо изучить параметры θ и обновить pθ, чтобы оптимизировать модель молекулярной сети. Поскольку представление узла было изучено GNNφ, GNNθ может на этой основе изучать информацию о молекулярной сети через механизм передачи сообщений. Более конкретно, GNNφ используется для генерации структурного представления g(0) в качестве начальных характеристик узла и ввода его в модель молекулярной сети для передачи сообщений. Аналогичным образом, здесь также можно рассматривать как процесс дистилляции знаний, где знания, полученные моделью GNNφ в масштабе атомной структуры, вводятся в модель GNNθ в масштабе молекулярной сети через все псевдометки, и мы используем наблюдаемые метки взаимодействия для модели. обучение.
Как показано на рисунке 1, на каждой итерации MUSE сначала выполняет шаг E для построения структурного графа для каждой пары взаимодействий, затем использует кодировщик структурного графа для создания представления графа белка или лекарства и использует предиктор взаимодействия для прогнозирования взаимодействий. данной пары биомолекул. Эта модель в масштабе атомной структуры объединяет взаимодействующие пары графов и моделирует распределение меток на основе структурных свойств. После оптимизации E-этапа структурное представление и граф взаимодействия передаются в модуль обмена сообщениями на уровне молекулярной сети. За M шагов информация распространяется по взаимодействиям в сети, изучая топологию сети и информацию о соседях. Поэтому MUSE итеративно обновляет два модуля на E-шаге и M-шаге, пока модель не сходится. Что еще более важно, одна из одношаговых моделей предоставляет взаимодействующие псевдометки для обучения другой в рамках взаимного контроля. Псевдометки, созданные в масштабе молекулярной сети, также можно использовать в качестве дополнения данных для моделей масштаба атомной структуры, тогда как псевдометки, созданные в масштабе атомной структуры, можно использовать для обучения моделей масштаба молекулярной сети путем добавления псевдоребер.
Текущие исследования показывают, что именно разная скорость обучения нейронных сетей в разных масштабах приводит к дисбалансу использования. Итеративная оптимизация атомной структуры и молекулярных сетей MUSE позволяет смягчить этот вредный дисбаланс и добиться более сильного обобщения в многомасштабных представлениях. Взаимный контроль гарантирует, что каждая масштабная модель обучается соответствующим образом, тем самым способствуя использованию эффективной информации в разных масштабах. Здесь для интерактивного обучения сети используется сеть изоморфизма графов (GIN), которая обладает выразительной способностью захватывать структуру графа и изучать информацию молекулярной сети.
Ограничение производительности задачи прогнозирования ссылок связано с неполнотой графа. С этой целью автор применил обучение псевдовероятности в рамках MUSE, расширил граф молекулярной сети псевдовзаимодействиями, предсказанными масштабной моделью атомной структуры GNNφ, мягко дополнил граф сети взаимодействий, а затем использовал модель молекулярной сети GNNθ для Более полные графики для окончательных прогнозов. Более того, стратегия была расширена до итеративного процесса оптимизации.
Авторы сравнили MUSE с некоторыми репрезентативными методами, как показано на рисунке 2. В этом исследовании для оценки использовались площадь под кривой ROC (AUROC), показатель F1 и площадь под кривой PR (AUPRC). Чем выше значение, тем лучше. В скобках в таблице указаны стандартные отклонения. Результаты показывают, что MUSE значительно улучшил прогнозирование ассоциации белок-белок, прогнозирование ассоциации лекарство-белок и прогнозирование ассоциации лекарство-лекарство по сравнению с существующими методами.
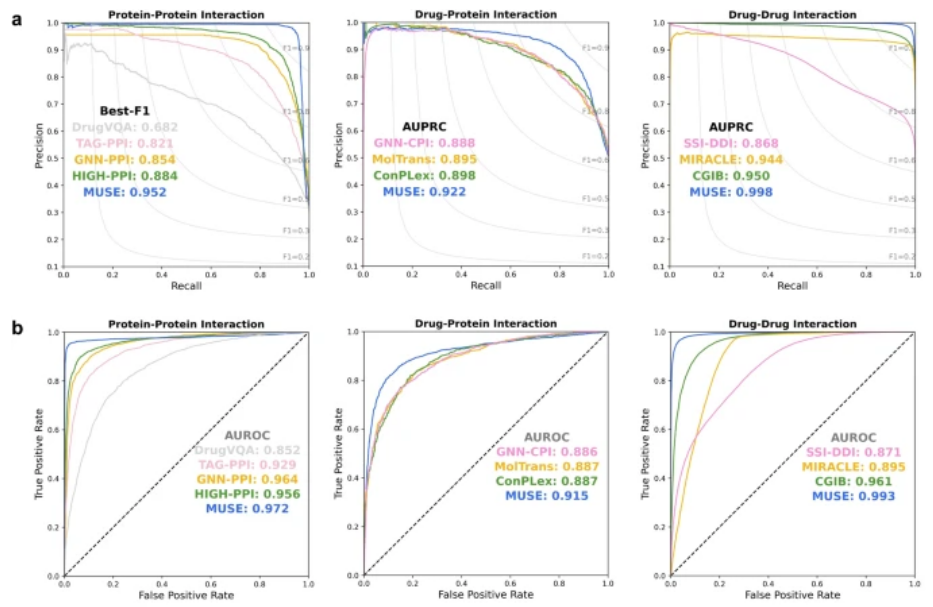
Рисунок 2. Сравнение с другими методами
Авторы разработали эксперименты по абляции, чтобы проверить эффективность конструкции модели. Авторы реализовали вариант MUSE, MUSE-joint, который использует совместное обучение (вместо использования алгоритма EM) для объединения процесса обучения многомасштабных сетей и сочетает в себе различные методы поиска (случайный поиск, поиск в ширину, поиск в глубину). -первый поиск) для прогнозирования белковых ассоциаций. Проверка набора данных, составленного в результате поиска). Оценка F1 соединения MUSE ниже, чем у полного MUSE, но поскольку он по-прежнему имеет структуру многомасштабной сети, его эффект по-прежнему выше, чем у других методов.
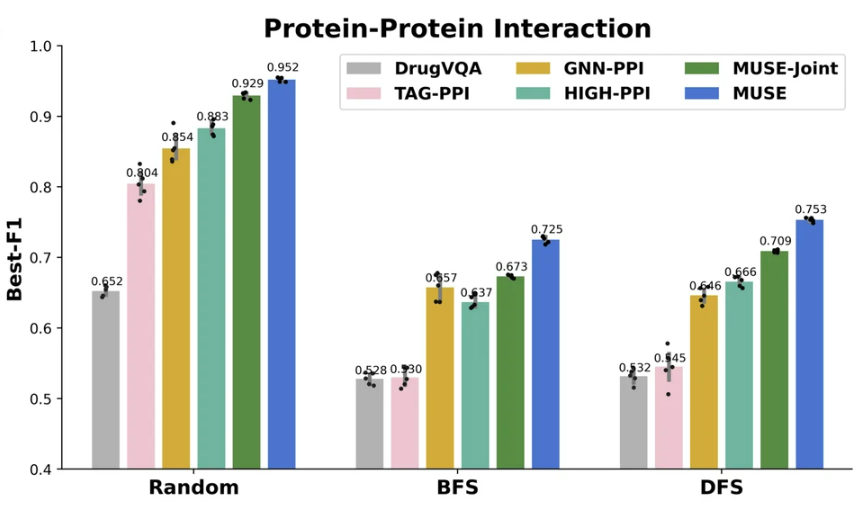
Рисунок 3. Эксперимент по абляции.
Автор также проводит анализ случаев. Чтобы лучше понять изученные многомасштабные представления, авторы изучили многомасштабные представления, изученные MUSE, с разных точек зрения, в том числе: (1) способность MUSE собирать информацию об атомной структуре, участвующую в PPI, и (2) взаимный контроль. между атомными структурами и представлениями молекулярных сетей, изученными MUSE.
Взяв в качестве примера предсказание сайта связывания (идентификатор PDB: 3CQQ-A), MUSE может точно идентифицировать остатки, принадлежащие сайту связывания (рис. 4а), с точностью 97,7%. Это говорит о том, что взаимный контроль в MUSE помогает моделям атомной структуры изучить ключевые подструктуры, имеющие отношение к взаимодействиям. Представление изученной атомарной структуры (рис. 4б) подтверждает, что изученное представление MUSE помогает различать типы взаимодействия, в то время как распределение HIGH-PPI близко к случайному и не позволяет эффективно использовать структурную информацию.
Проиллюстрировать роль взаимного контроля,Авторы провели исследования абляции.,Изучить влияние псевдометок, предсказанных на уровне атомной структуры, на молекулярном уровне. Авторы рассчитали лучшие показатели F1 при различных порогах псевдомаркировки в наборе данных PPI (Рисунок 4c). Без взаимного контроля (t=0),Лучший F1 модели — 0,908.,Лишь немного лучше, чем базовый метод (0,886,ВЫСОКИЙ PPI). По мере увеличения порога t,Лучший результат MUSE в Формуле-1 быстро улучшается. Это улучшение связано с добавлением большего количества псевдовзаимодействий в PPIсеть.,Тем самым смягчается неполнота сети. но,когдаt>0.4час,По мере увеличения порога t,Производительность постепенно снижается,показыватькогдаt>0.4час,Предсказанные ложные взаимодействия становятся все более шумными.
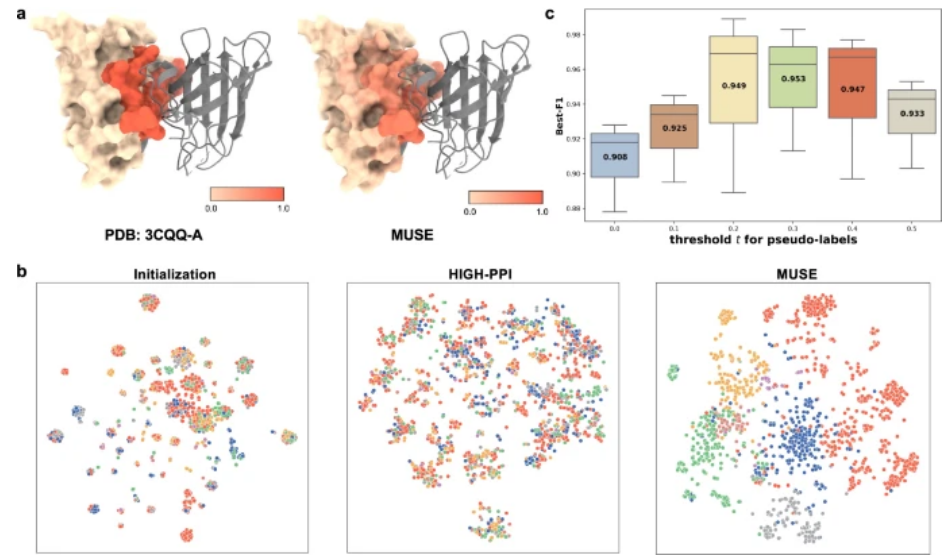
Рисунок 4. Анализ случая
В этой работе авторы предлагают MUSE, который объединяет два масштаба биомолекул, масштаб атомной структуры и масштаб молекулярной сети, в многомасштабную структуру. Итеративная оптимизация, основанная на вариационном алгоритме EM, значительно улучшает возможности обучения многомасштабных представлений, позволяя MUSE выполнять многомасштабное изучение белков и лекарств, и может быть распространена на другие многомасштабные задачи.
Поскольку многомасштабные данные продолжают расти, интеграция межмасштабных данных становится все более важной. MUSE обеспечивает эффективную перспективу интеграции неравновесных многомасштабных данных, подчеркивая преимущества интеграции информации в масштабе атомной структуры в прогнозы молекулярных взаимодействий. Кроме того, обучение в масштабе молекулярной сети в MUSE дает ценную информацию о дальнейшей оптимизации моделей атомной структуры для улучшения характеристик белков.
Хотя MUSE продемонстрировал современную производительность в экспериментах, его способность справляться с шумными и неполными многомасштабными последующими задачами все еще может быть улучшена в будущем. Этого можно достичь путем объединения предшествующих знаний с помощью графиков знаний и объяснимых методов искусственного интеллекта. С другой стороны, MUSE также демонстрирует потенциал для распространения на другие масштабы для вычислительного открытия лекарств, углубляя понимание множества структурных уровней молекул и способствуя эффективному открытию лекарств.
Ссылки:
Rao et al. A variational expectation-maximization framework for balanced multi-scale learning of protein and drug interactions. Nat Commun. 2024
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
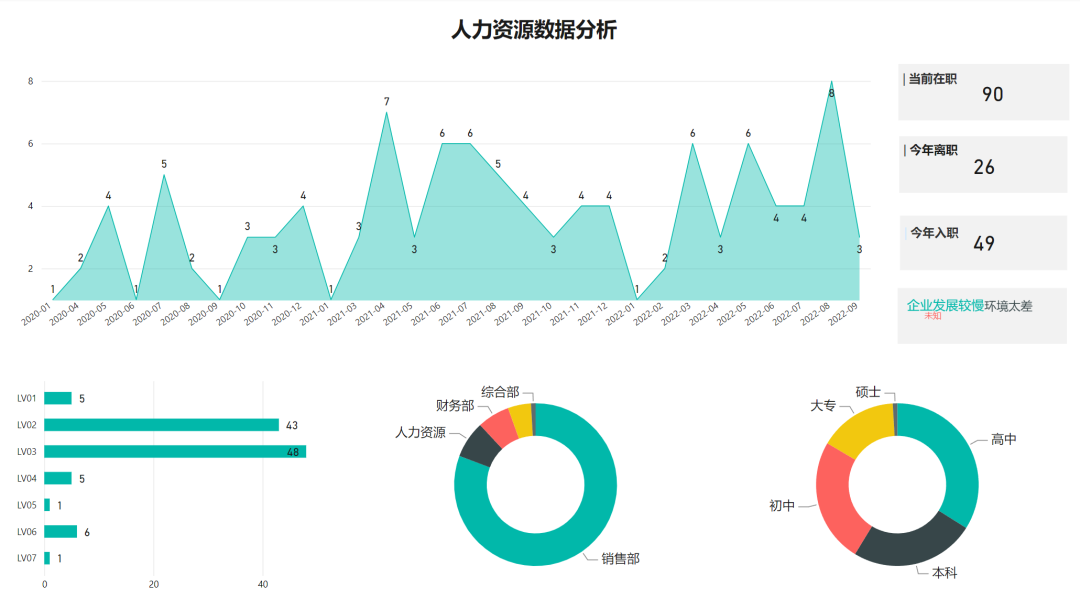
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
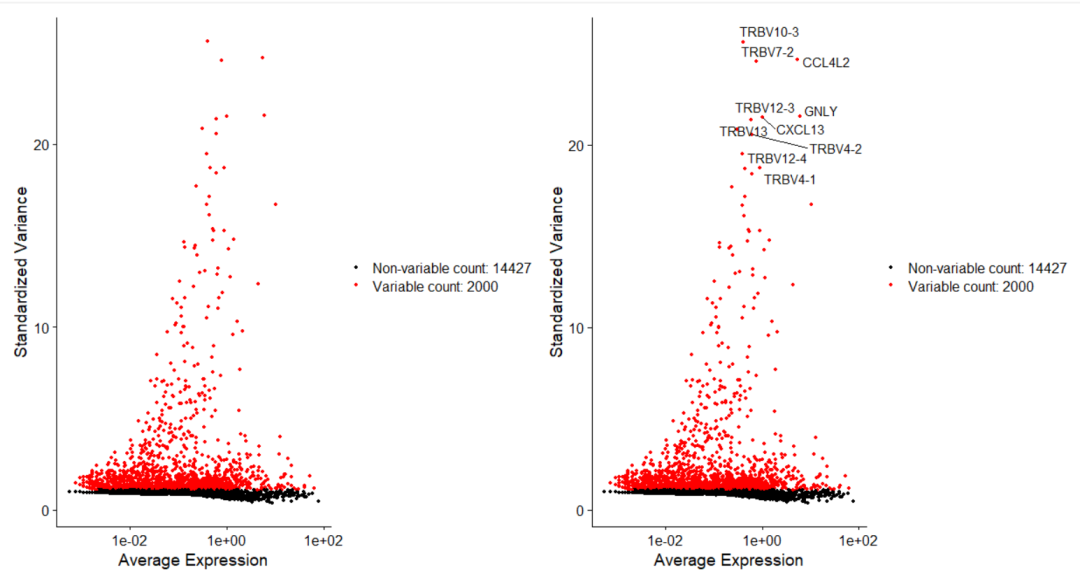
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
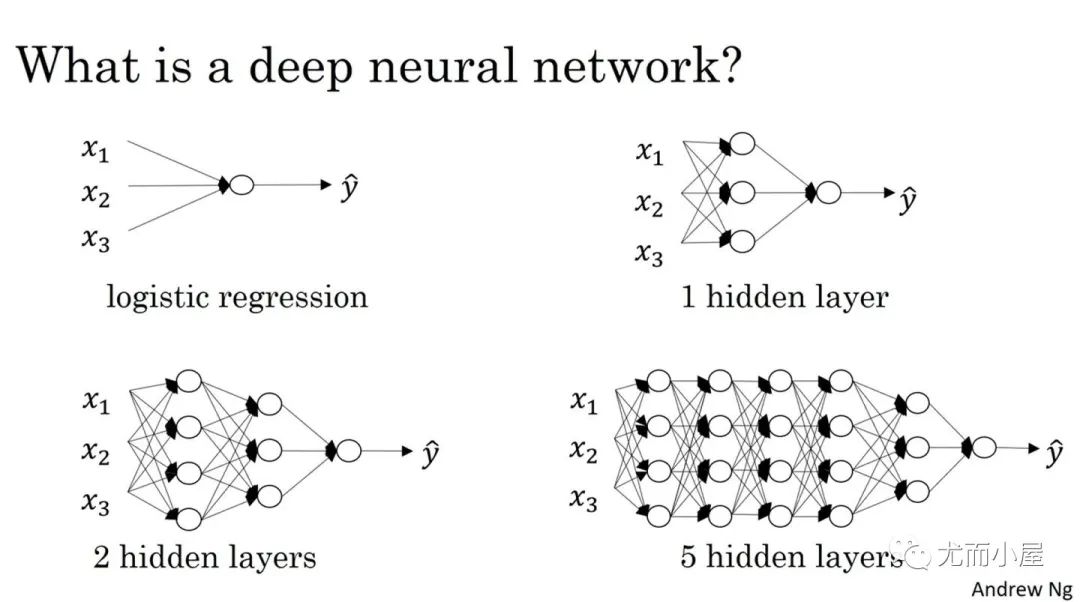
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


