[Калибровка датчика] Калибровка внешних параметров камеры и радара (теория и код)
Предисловие
1. Калибровка внешних параметров камеры требует предварительного знания внутренних параметров камеры. Калибровка внутренних параметров камеры здесь подробно не обсуждается. 推荐一篇博客Компьютерное зрение (калибровка камеры; внутренние параметры; внешние параметры; коэффициент искажения
2. Математическая задача преобразования внешних параметров калибровки: расчет поворота и перевода из одной трехмерной системы координат в другую трехмерную систему координат.
3、Ссылка на схему калибровкиБумажный адрес。Фактическое сравнение калибровки,Этот метод обладает высокой точностью и прост в эксплуатации.
4. Цель: Опубликуйте виртуальное изображение цели:

(Фактическая цель должна быть сделана самостоятельно в соответствии с потребностями)
1. Калибровка внешних параметров камеры.
1.1. идентификация апритага
1. Разместите метки по четырем углам мишени.
2. Определите четыре тега и получите координаты в системе координат изображения.
def calibration_point(self):
img_gray = cv2.cvtColor(self.image, cv2.COLOR_BGR2GRAY)
detector = apriltag.Detector(searchpath=["./"])
results = detector.detect(img_gray)
markerCenter = []
for i in range(len(results)):
tmp_obj = results[i]
markerCenter.append(list(tmp_obj.center))
return markerCenter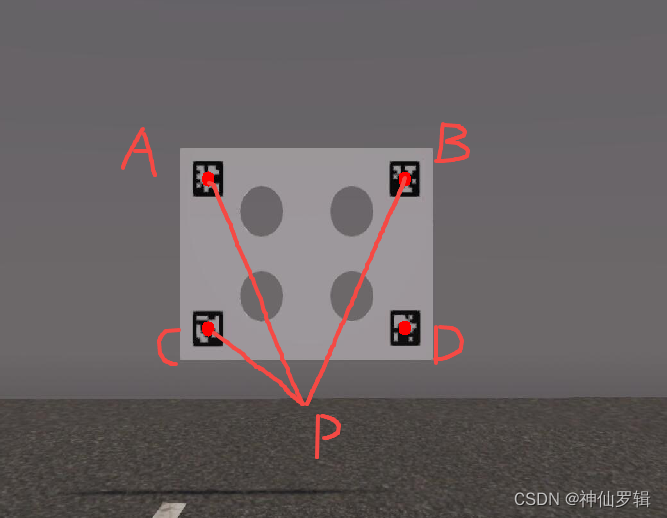
1.2. Найдите орты в направлениях ПА, ПБ и ПК в системе координат камеры.
Отношения преобразования между координатами пикселей и координатами камеры
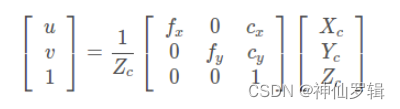
Возьми Zc = 1 . но x, y, z = (u − cx)/fx, (v − cy)/fy, 1
После нормализации можно получить единичные векторы PA, PB, PC.
1.3. Найдите угол APB, угол BPC, угол CPA.
Угол APB, угол BPC и угол CPA легко найти по векторам PA, PB и PC.
Пример: cos(угол APB) = PA .PB
1.4. Найдите длины ПА, ПБ и ПК.
Математическая задача преобразования: тетраэдр PABC, зная длины AB, AC, BC, угол APB, угол BPC и угол CPA, найти длины PA, PB и PC.
Решение можно найти, зная условные уравнения одновременности. Можно решить методом исключения
Справочник по выводу формул:метод исключения
Уравнения устанавливаются посредством теоремы косинусов, и после преобразования получается система квадратных уравнений двух переменных.
При решении методом исключения может быть четыре группы решений.
def solve_for_length(self, threePoint):
solution = [] # Сохраненное решение
lenAB, lenBC, lenCA = self.w, self.h, np.sqrt(self.w * self.w + self.h * self.h)
p, q, r = self.get_three_point_r(threePoint)
p, q, r = 2 * p, 2 * q, 2 * r
a, b = np.power(lenAB / lenCA, 2), np.power(lenBC / lenCA, 2)
a2, b2, p2, q2, r2, pr = a * a, b * b, p * p, q * q, r * r, p * r
pqr = q * pr
if p2 + q2 + r2 - pqr - 1 == 0: # Четыре точки лежат в одной плоскости и решения нет.
return «Четыре точки лежат в одной плоскости, решения нет»
ab, a_2, a_4 = a * b, 2 * a, 4 * a
A = -2 * b + b2 + a2 + 1 + ab * (2 - r2) - a_2
B = q * (-2 * (ab + a2 + 1 - b) + r2 * ab + a_4) + pr * (b - b2 + ab)
C = q2 + b2 * (r2 + p2 - 2) - b * (p2 + pqr) - ab * (r2 + pqr) + (a2 - a_2) * (2 + q2) + 2
D = pr * (ab - b2 + b) + q * ((p2 - 2) * b + 2 * (ab - a2) + a_4 - 2)
E = 1 + 2 * (b - a - ab) + b2 - b * p2 + a2
temp = (p2 * (a - 1 + b) + r2 * (a - 1 - b) + pqr - a * pqr)
b0 = b * temp * temp
if b0 == 0: # Когда b0=0, найдите y=0 Не соответствует смыслу вопроса
return «y=0, нет решения»
unknownX = sympy.symbols('x') # Решите для х
solve = sympy.solve(A * unknownX ** 4 + B * unknownX ** 3 + C * unknownX ** 2 + D * unknownX + E, unknownX)
n = len(solve) # Определите количество решений. Если корней несколько, засчитывается один.
if n == 0:
return «x не имеет корня и решения»
r3, pr2 = r2 * r, p * r2
r3q = r3 * q
inv_b0 = 1.0 / b0
for i in range(n):
x = solve[i]
if abs(np.imag(complex(x))) < 1e-10:
x = np.real(complex(x))
else:
continue
if x < 0: # Если оно не соответствует смыслу вопроса, отбросьте это решение.
continue
x2 = x * x
b1 = ((1 - a - b) * x2 + (q * a - q) * x + 1 - a + b) * (((r3 * (a2 + ab * (2 - r2) - a_2 + b2 - 2 * b + 1))
* x + (r3q * (2 * (b - a2) + a_4 + ab * (r2 - 2) - 2) + pr2 * (1 + a2 + 2 * (ab - a - b) + r2 *
( b - b2) + b2))) * x2 + (r3 * (q2 * (1 - 2 * a + a2) + r2 * (b2 - ab) - a_4 + 2 * (a2 - b2) + 2) +
r * p2 * (b2 + 2 * (ab - b - a) + 1 + a2) + pr2 * q * (a_4 + 2 * (b - ab - a2) - 2 - r2 * b)) * x +
2 * r3q * (a_2 - b - a2 + ab - 1) + pr2 * (q2 - a_4 + 2 * (a2 - b2) + r2 * b + q2 * ( a2 - a_2) + 2)
+ p2 * (p * (2 * (ab - a - b) + a2 + b2 + 1) + 2 * q * r * (b + a_2 - a2 - ab - 1))))
if b1 <= 0: # искатьy<0 Откажитесь от этого решения
continue
y = inv_b0 * b1
v = x * x + y * y - x * y * r
if v < 0: # Решения меньше 0 не соответствуют
continue
lenPB = lenCA / np.sqrt(v)
lenPC = x * lenPB
lenPA = y * lenPB
solution.append([lenPA, lenPB, lenPC]) # Решения, соответствующие условиям
return solution1.5. Разложение SVD для решения матрицы вращения и перемещения.
Согласно 1.4 получаются координаты четырех групп точек А, В и С в системе координат камеры.
Рассчитайте четыре набора матриц вращения и перемещения посредством разложения svd.
svdаварияматематикассылка на деривацию:SVD-разложение и вывод
Рассчитайте ошибку перепроецирования точки D после вращения и перемещения и выберите точку с наименьшей ошибкой перепроецирования в качестве окончательного результата калибровки.
def get_rt(childList, parentList):
x = get_data(childList)
y = get_data(parentList)
zeroMatrix = np.zeros((3, 3))
for i in range(y.shape[0]):
newY = y[i].reshape(1, y.shape[1])
newX = x[i].reshape(1, y.shape[1])
zeroMatrix = zeroMatrix + newX.T @ newY
svd = np.linalg.svd(zeroMatrix)
U, E, V = svd
midMatrix = np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, np.linalg.det(V.T @ U.T)]])
r = V.T @ midMatrix @ U.T
t = get_avg(parentList).T - r @ get_avg(childList).T
return r, t2. Калибровка внешних параметров радара, комбинация радара и камеры.
2.1. Получите калибровочную плату через радар.
# Подгоняющая плоскость наименьших квадратов ax + by + cz - 1 = 0
def fit(M):
np_ones = np.ones((len(M), 1))
M_T = M.transpose()
result = np.dot(np.dot(np.linalg.inv(np.dot(M_T, M)), M_T), np_ones)
return resultdef get_plane(self, count):
pcd = o3d.io.read_point_cloud(self.path[-1])
cloud_point = np.asarray(pcd.points)
minX, maxX, minY, maxY, minZ, maxZ = self.fiter
points, point_x, point_z = [], [], []
for point in cloud_point:
if minX < point[0] < maxX and minY < point[1] < maxY and minZ < point[2] < maxZ:
points.append(list(point))
point_x.append(point[0])
point_z.append(point[2])
min_z, max_z, avg_x = min(point_z), max(point_z), np.average(point_x)
gap = 0.02
sum_max, sum_min = 0, 0
while sum_max < count or sum_min < count:
if sum_max < count:
sum_max = 0
max_z -= gap
if sum_min < count:
sum_min = 0
min_z += gap
for data in point_z:
if max_z - gap < data < max_z + gap:
sum_max += 1
if min_z - gap < data < min_z + gap:
sum_min += 1
result_cloud_point = []
for path in self.path:
pcd = o3d.io.read_point_cloud(path)
cloud_point = np.asarray(pcd.points)
for point in cloud_point:
if minX < point[0] < maxX and minY < point[1] < maxY and min_z - gap < point[2] < max_z + gap:
result_cloud_point.append(point)
a, b, c = fit(np.array(result_cloud_point)).reshape(-1)
for i in range(len(result_cloud_point) - 1, 0, -1):
x, y, z = result_cloud_point[i]
if np.abs(a * x + b * y + c * z - 1) / np.sqrt(a * a + b * b + c * c) > 0.03:
del result_cloud_point[i]
return result_cloud_pointНа относительно открытом пространстве легко получить примерное расположение калибровочной платы.

2.2. Найдите центральную точку установочного круга.
def circle_fit(self, point_list, A):
M, L = [], []
for i in range(len(point_list) - 1):
x1, y1, z1 = point_list[i]
x2, y2, z2 = point_list[i + 1]
M.append([x2 - x1, y2 - y1, z2 - z1])
l = (x2 * x2 + y2 * y2 + z2 * z2 - (x1 * x1 + y1 * y1 + z1 * z1)) / 2
L.append(l)
B = np.array(M)
L2 = np.array(L).reshape(len(L), 1)
B_T = B.transpose()
A_T = A.transpose()
left = np.vstack((np.hstack((np.dot(B_T, B), A)), np.hstack((A_T, np.array([0]).reshape(1, 1)))))
right = np.vstack((np.dot(B_T, L2), np.array([1]).reshape(1, 1)))
C = np.dot(np.linalg.inv(left), right)
center_x, center_y, center_z = C[0][0], C[1][0], C[2][0]
return center_x, center_y, center_z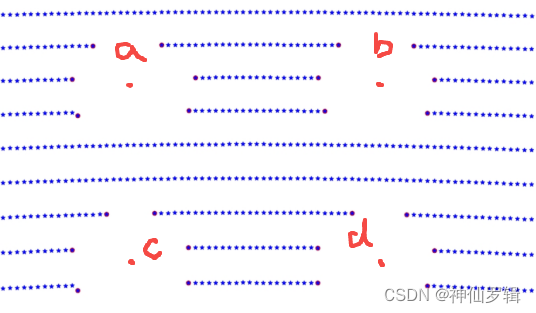
2.3. Совместная калибровка камеры и радара.
Поскольку мы знаем модель калибровочной пластины, мы можем вычислить координаты ABCD в системе координат радара через abcd (обратите внимание на взаимно однозначное соответствие), а также вычислить матрицу вращения и перевода от камеры к радару через svd-разложение.
2.4. Внешние параметры РЛС.
Определите мировую систему координат (корпус транспортного средства) и узнайте координаты a, b, c, d в мировой системе координат, и можно легко рассчитать внешние параметры радара.
3. Меры предосторожности при реальной эксплуатации
1. В зависимости от места установки радара высота и расстояние до калибровочной доски также должны быть разными. После определения они должны оставаться неизменными.
2. Разные модели радаров имеют разные трудности с определением центральной точки круга. Иногда проблему невозможно увидеть полностью или жгута проводов недостаточно. Для решения проблемы можно использовать соответствующие алгоритмы.
3. Если вы рассчитываете вращение и перемещение только на основе точки-точки. Будет некоторая ошибка в угле. Угловую ошибку можно итеративно оптимизировать посредством аппроксимации плоскости и векторов нормалей.
4. Результаты калибровки данного метода,Ошибка перепроецирования камеры<1Пиксель,Вращение радара практически безошибочно,Ошибка трансляции радара — это, по сути, ошибка самого радара.
4. Справочные ссылки
1、https://blog.csdn.net/QYJ_WORKHARDING/article/details/124867821
2、https://arxiv.org/pdf/1705.04085.pdf
3、https://zhuanlan.zhihu.com/p/140077137
4、https://zhuanlan.zhihu.com/p/108858766

Дополнительные правила вознаграждения для послов промоакций в феврале 2023 г.

Встряхните людей! Ищем представителей класса Double Eleven в техническом кругу через Интернет! Участвуйте в конкурсе эссе и выигрывайте призы каждую неделю

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
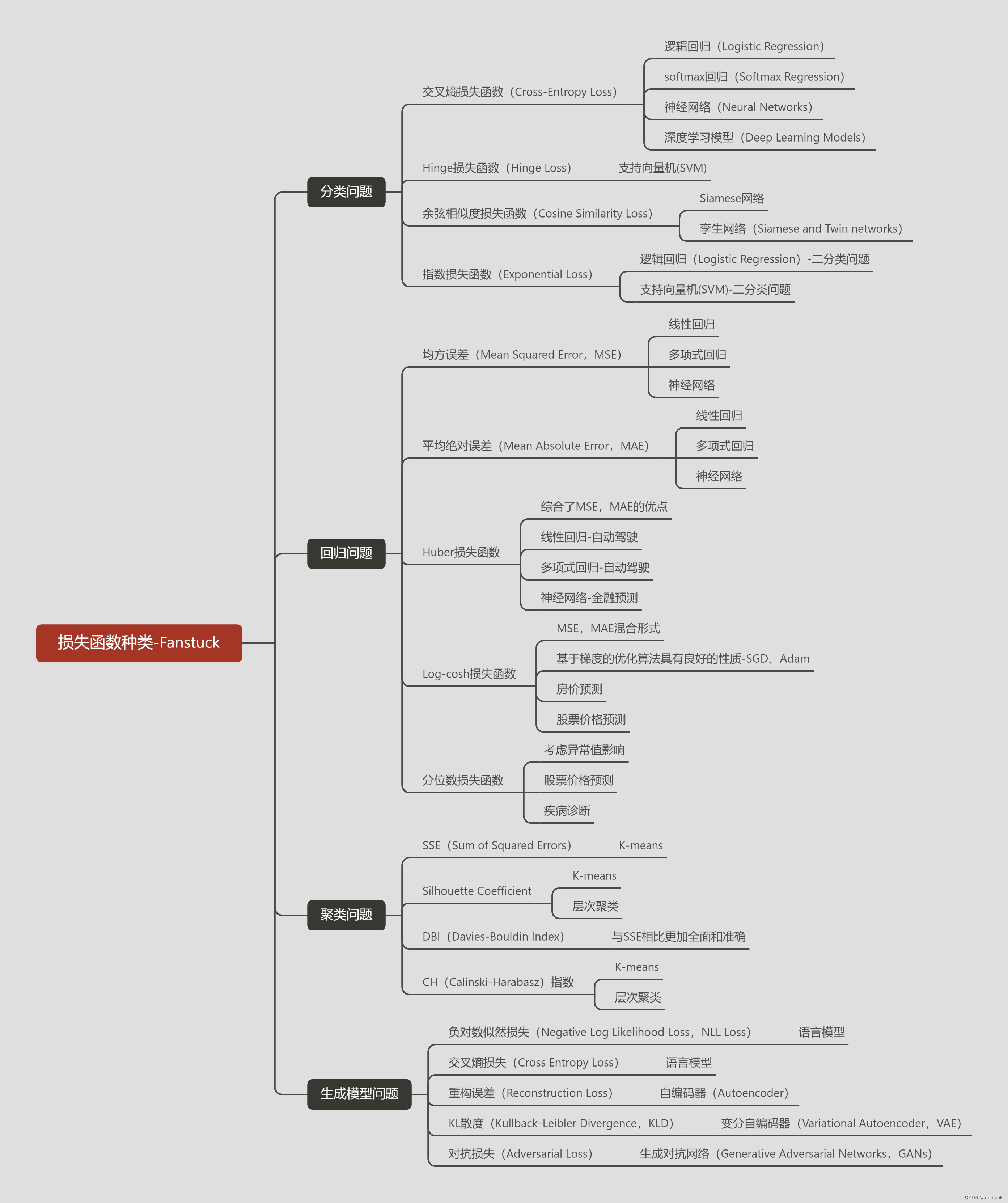
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
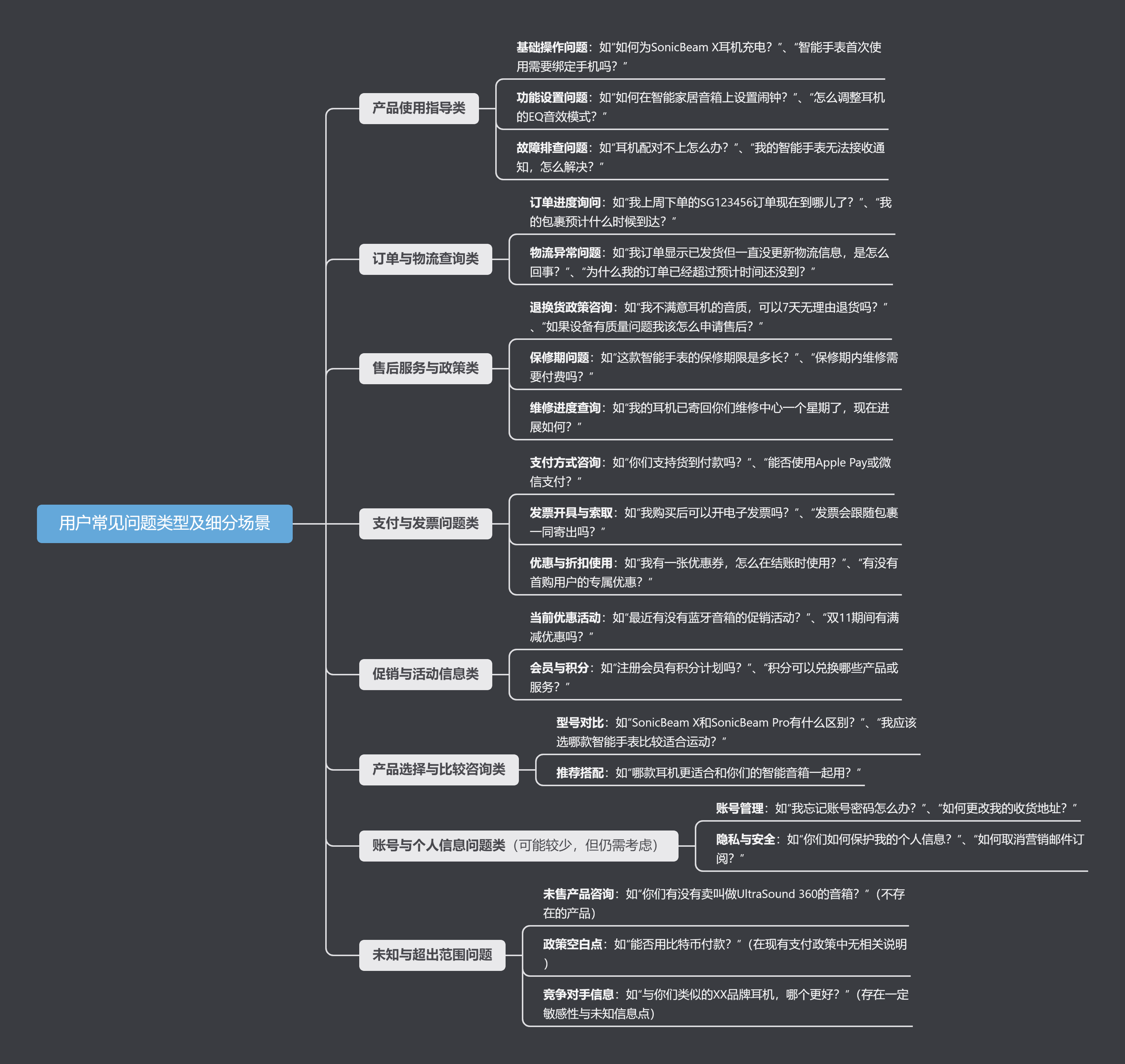
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!


