Как работает память ECC сервера
Привет всем, я Фей Ге!
Прежде чем начать сегодняшний рассказ, я сначала покажу вам два модуля памяти 1R*8.
Все современные процессоры являются 64-битными, и каждая связь с памятью требует передачи 64-битных данных. 1R в типе памяти 1R * 8 означает, что модуль памяти имеет только один ранг, а 8 означает, что каждая частица памяти предоставляет 8 бит данных во время каждого 64-битного процесса ввода-вывода в память. При таком расчете 64-битные данные требуют объединения 8 частиц памяти.


Почему из этих двух модулей памяти один имеет 8 микросхем, а другой — 9? Эта история также начинается с переворачивания битов.
1. Переключение битов и память ECC.
Когда наш компьютер работает, процессору всегда необходимо взаимодействовать с памятью. Однако в процессе взаимодействия с вероятностью может произойти инвертирование битов из-за помех со стороны окружающих электромагнитных полей.
По статистике, на карте памяти емкостью 8 ГБ в среднем случается 1 – 5 таких ошибок в час.
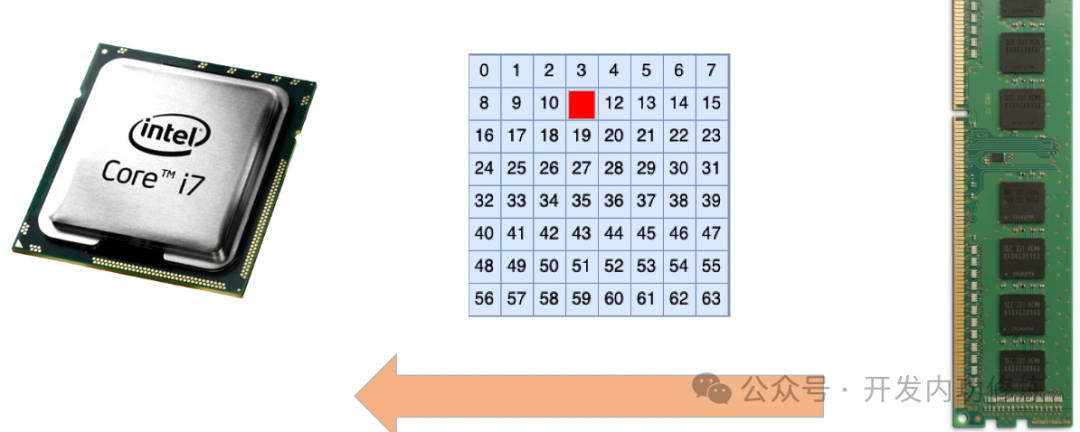
Когда мы используем персональные компьютеры для работы, память в основном используется для обработки таких данных, как изображения и видео. Даже если в памяти произойдет небольшой переворот, он может повлиять только на одно значение пикселя, что сложно почувствовать и оно не оказывает большого влияния. Даже если переключение битов действительно происходит в критическом системном коде и вызывает проблемы в работе, это не имеет большого значения и может быть решено путем перезапуска системы.
Но в серверных приложениях обычно обрабатываются очень важные вычисления, которыми может быть транзакция заказа или депозит. Кроме того, серверам часто приходится работать непрерывно месяцами, а то и годами, и решить проблему перезагрузкой невозможно. Таким образом, сервер имеет низкую устойчивость к ошибкам переворота битов. Существует потребность в технических решениях, которые могут в определенной степени решить проблему переворота битов.

ECC — это такая технология памяти. Его полное английское название — «Проверка и исправление ошибок», а соответствующее китайское название — «Проверка и исправление ошибок». Как видно из названия, ECC может не только находить ошибки в памяти, но и исправлять их.
По сравнению с памятью персонального компьютера, в которой не используется технология ECC, для хранения данных можно использовать все частицы памяти. Каждые 64 бита данных в памяти ECC требуют дополнительных 8 бит данных в качестве проверочных битов, которые помогают обнаруживать или исправлять ошибки.
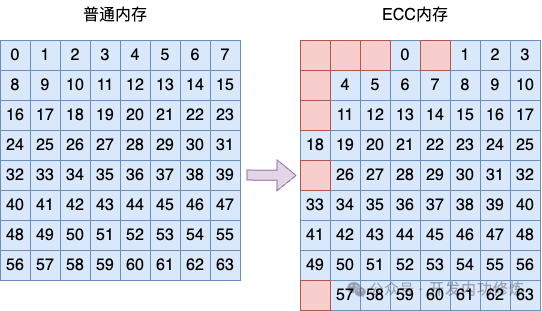
Итак, у нас есть ответ на первый вопрос. Все частицы на обычной карте памяти используются для хранения реальных данных. Помимо данных, память ECC также должна хранить 8-битные контрольные биты.
В обычной памяти 1R*8 достаточно 64/8=8 частиц. Однако для ввода-вывода в памяти ECC необходимо передать 72 бита данных, поэтому всего требуется 72/8 = 9 частиц памяти.
Проблема выяснена. Но стиль нашего публичного отчета «Развитие внутренней силы» заключается не только в том, чтобы знать, но и понимать принципы. Итак, давайте перейдем к рассмотрению того, как работает алгоритм исправления ошибок ECC.
2. Принцип коррекции ошибок ECC
Так почему же память ECC может обнаруживать и исправлять ошибки с помощью дополнительных 8 бит избыточных проверочных данных? Давайте сначала рассмотрим простейшую проверку четности.
2.1 Простая проверка четности
Для обнаружения переворота одного бита можно использовать простую проверку четности. Обратите внимание, что ключевыми ключевыми словами являются «обнаружение» и «один бит». Этот алгоритм можно использовать только для обнаружения, а не для исправления ошибок. И он эффективен только для переворота одного бита и не может справиться с ситуацией одновременного переворота двух битов.
Принцип заключается в добавлении 1 бита данных перед отслеживаемыми данными, чтобы гарантировать, что количество единиц во всем двоичном массиве (включая проверочный бит) является четным числом.
Например, ниже приведен 8-битный двоичный массив.
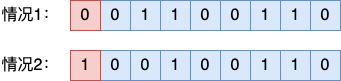
Для случая 1:Предположим, оригиналданные Уже есть четное число 1 , поэтому контрольная цифра установлена на 0 Вот и все, в целом 1 Число - четное число.
Для случая 2:Предположим, оригиналданныесередина 1 Число нечетное, поэтому контрольную цифру необходимо установить на 1 , чтобы гарантировать, что весь массив 1 Число - четное число Контрольная цифра В не является реальными данными пользователя, поэтому она не влияет на правильное чтение данных.
В общем, в двоичном массиве с добавленной 1-битной контрольной цифрой количество единиц всегда будет четным при правильных обстоятельствах.
Если перевернуть 1 бит, это неизбежно приведет к тому, что количество единиц в двоичном массиве станет нечетным числом. Таким образом, мы можем узнать, произошел ли одиночный переворот бита, наблюдая за тем, является ли количество единиц в данных четным числом.
Поняв принцип, вы также узнаете о двух ограничениях простой проверки четности, упомянутых ранее.
- Во-первых, мы можем только обнаружить, что что-то пошло не так, но не знаем, где произошла ошибка, поэтому не можем ее исправить.
- Во-вторых, он может обнаруживать только однобитовые перевороты и ничего не может сделать с двухбитовыми переворотами.
2.2 Введение в код Хэмминга
Чтобы решить проблему исправления ошибок и двух ошибок в данных, Ричард Хэмминг в 1950 году предложил алгоритм проверочного кода Хэмминга, основанный на простом алгоритме проверки четности. Сам Ричард Хэмминг получил премию Тьюринга в 1968 году за этот алгоритм. Хотя прошло уже более 70 лет, он до сих пор широко используется в памяти ECC серверов.
Первое, что следует сказать, это то, что коды Хэмминга имеют ограничения. Для следующих ситуаций:
- если в битовых данных происходит одиночный переворот бита,Код Хэмминга может не только обнаруживать возникновение ошибок,Также умеет находить место ошибок и исправлять их.
- если произошли два переворота битов,Код Хэмминга может только обнаруживать ошибки. Но я не могу найти конкретное место и не могу исправить ошибку.,Решить проблему можно только повторной передачей.
- еслислучилось 3 Если один или несколько битов перевернуты, код Хэмминга будет бесполезен.
На практике вероятность того, что 3 или более бита 64-битных данных появятся в памяти одновременно, очень и очень мала. Кроме того, память должна быть достаточно быстрой в работе. При аппаратной реализации кода Хэмминга потеря производительности составляет всего около 2–3%. Поэтому, хотя код Хэмминга не может справиться с инвертированием битов более чем на 3 бита, он по-прежнему широко используется при проверке ошибок и исправлении серверной памяти. Из-за различных сценариев применения жесткие диски SSD используют коды LDPC, которые поддерживают коррекцию ошибок многобитной контрольной суммы.
Поскольку память ECC, основанная на кодах Хэмминга, не может обрабатывать 3-битные перевороты и более, специальным направлением в области мер противодействия безопасности является изучение того, как намеренно создавать 3-битные перевороты в памяти для достижения атакующего поведения. И как противостоять 3-битным флип-атакам.
2.3 Разработка алгоритма кода Хэмминга
Основная идея разработки алгоритма проверочного кода Хэмминга заключается в установке большего количества контрольных цифр.,а затем использоватьперекрестная проверкаспособ реализовать позиционирование битов ошибок。
Код Хэмминга содержит 64 бита пользовательских данных и 8 бит избыточного проверочного кода, то есть всего имеется 72 бита данных. Эти 72-битные данные можно рассматривать как двумерную матрицу с 9 строками и 8 столбцами.
Первый уровень проверки — это бит проверки битов в верхнем левом углу матрицы, который используется для реализации проверки четности всей матрицы.
Второй уровень проверки — проверка группировки столбцов. В столбце используются 3 метода для разделения 8 столбцов на разные дихотомические группы. Каждая группа имеет бит четности для реализации проверки четности всей группы.
Первый метод группировки столбцов заключается в том, чтобы рассматривать столбцы 2, 4, 6 и 8 как группу и размещать бит в этой группе в качестве контрольного кода.
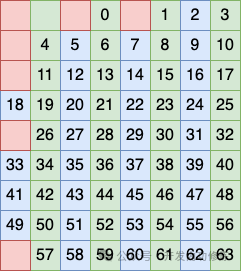
Второй метод группировки столбцов заключается в том, чтобы рассматривать столбцы 3, 4, 7 и 8 как группу и размещать бит в этой группе в качестве проверочного кода.
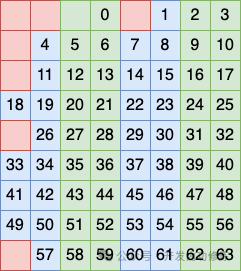
Третий метод группировки столбцов заключается в том, чтобы рассматривать столбцы 5, 6, 7 и 8 как группу и размещать бит в этой группе в качестве контрольного кода.
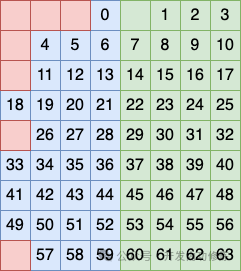
Таким образом, эти три метода группировки переплетаются, и каждый содержит частичные столбцы другой группировки.
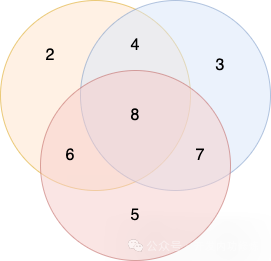
Третий уровень — проверка группировки строк. Поскольку строк на одну больше, чем столбцов, для простой проверки четности используются 4 группы.
Первый метод группировки строк состоит в том, чтобы рассматривать строки 2, 4, 6 и 8 как группу и размещать бит в этой группе в качестве проверочного кода.
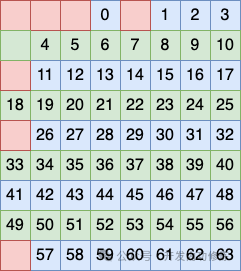
Второй метод группировки строк заключается в том, чтобы рассматривать строки 2, 3, 7 и 8 как группу и размещать бит в этой группе в качестве проверочного кода.
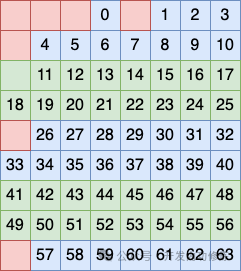
Третий метод группировки строк заключается в том, чтобы рассматривать строки 5, 6, 7 и 8 как группу и размещать бит в этой группе в качестве контрольного кода.
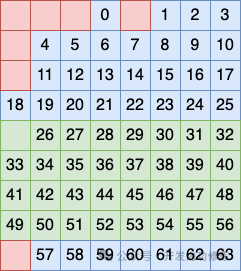
Третий метод группировки строк заключается в том, чтобы рассматривать оставшуюся 9-ю строку как группу отдельно, а также размещать бит в этой группе как проверочный код.
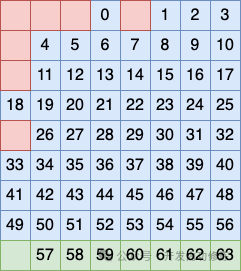
Вышеизложенное представляет собой принцип построения алгоритма кода Хэмминга.
2.4 Коррекция одиночных ошибок переворота кода Хэмминга
Далее давайте посмотрим, как алгоритм кода Хайминга реализует обнаружение и исправление ошибок при перевороте одного бита. Мы предполагаем, что в этих данных происходит одноразрядный переворот. Если быть более конкретным, например, бит № 30 пользовательских данных неправильный.
В это время можно проверить все биты первого уровня.Обнаружена небольшая ошибка。Но я еще не знаю, где это произошло。
Затем используйте проверку группировки столбцов второго уровня.
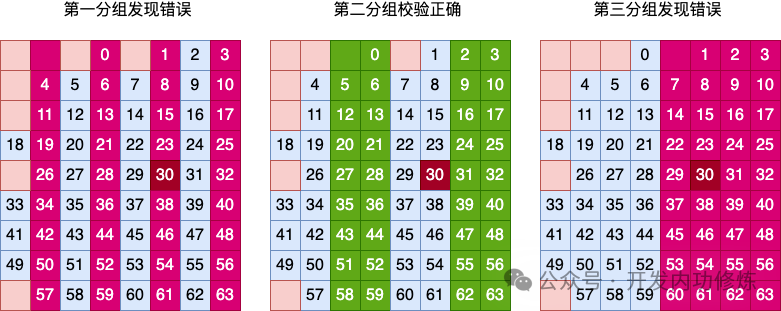
в ответ с Когда три группы Список проверяются отдельно,В первом методе группировки Список обнаружена ошибка.,Пройдена вторая проверка метода группировки Список,третий Список Обнаружена ошибка при проверке метода группировки。в соответствии с Отношения включения между каждой группой позволяют сделать вывод, что ошибка произошла в 6 Список。
Затем выполните проверку группировки строк третьего уровня.
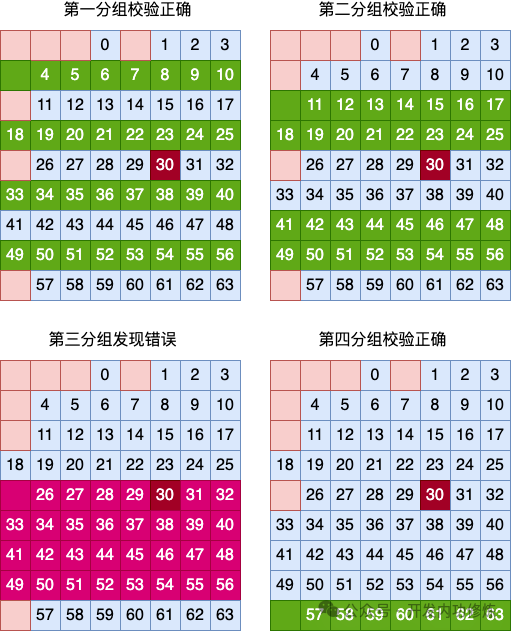
Пройдена первая верификация группы ХОРОШО、Пройдена вторая проверка группы ХОРОШО、Третья проверка группы ХОРОШО не удалась、четвертый ХОРОШОПроверка группы пройдена。Такв соответствии перекрестная связь группировки с ХОРОШО, можно сделать вывод, что ошибка данных произошла в 5 ХОРОШО。
В сочетании с результатами проверки группировки столбцов, приведенными выше, можно сделать вывод, что данные в строке 5 и столбце 6 неверны. Поскольку двоичные данные имеют только два значения: 0 и 1, ошибки можно исправить, если они обнаружены. Это принцип реализации кода Хэмминга для проверки и исправления однобитовых ошибок.
2.4. Обнаружение двухбитовых ошибок в кодах Хэмминга.
Код Хэмминга может исправлять однобитные ошибки, но в то же время для двухбитных ошибок он может только обнаружить ошибку, и нет способа определить местонахождение ошибки, поэтому исправление ошибок невозможно.
Предположим, что ошибки возникают в 29-м и 30-м битах пользовательских данных. Значит, поскольку две ошибки произошли одновременно, проверка во всей матрице не должна быть найдена, и проверка проходит.
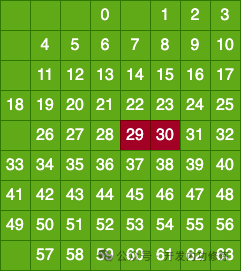
Давайте еще раз посмотрим на результаты проверки колонок.
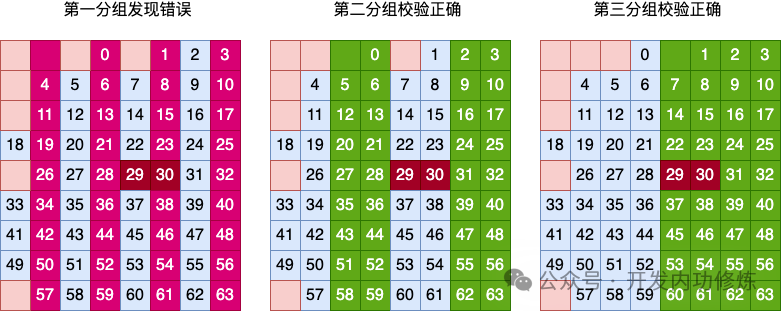
В первой группе обнаружена ошибка, проверка во второй группе правильна, проверка в третьей группе правильна (простая проверка на четность не может обнаружить двухбитные ошибки), затем перекрестная проверка группы столбцов делает вывод, что произошла ошибка произошло в столбце 2. Очевидно, ошибка двух переворотов битов привела к неправильному заключению проверки группировки столбцов.
Посмотрим на результаты проверки.
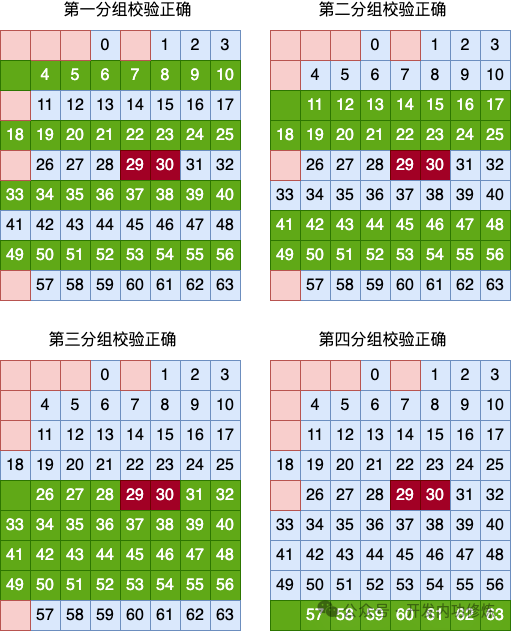
Все результаты проверки группировки строк верны. Два переворота битов также приводят к сбою четности строк.
Тогда 1) вывод полной проверки матрицы - отсутствие ошибки, 2) вывод проверки группировки столбцов - ошибка во втором столбце, 3) вывод проверки группировки строк - отсутствие ошибки. ошибка.
Три вывода проверки не совпадают, что говорит о том, что произошла ошибка, но их больше одного。
Код Хэмминга обнаружил ошибку, но не смог определить ее конкретное место. Когда это произойдет, данные, возвращаемые этим вводом-выводом в память, будут недействительны, и их можно будет прочитать снова.
Следует отметить, что код Хэмминга может быть ошибочно принят за правильный, если 3 и более бита ошибочны. Однако, поскольку вероятность возникновения трехбитных ошибок одновременно в 64 битах слишком мала, коды Хэмминга по-прежнему широко используются в серверной ECC-памяти.
Подвести итог
Вначале мы видели две карты памяти: одну с 8 черными чипами, а другую с 9 чипами памяти. Это связано с тем, что в дополнение к каждый раз предоставлению 64-битных пользовательских данных в ЦП память ECC также должна предоставлять дополнительные 8-битные данные в качестве избыточного контрольного бита. Функция этих избыточных проверочных битов заключается в обнаружении и исправлении однобитовых ошибок. В случае двухбитовых ошибок ошибки могут быть обнаружены, но ошибки не могут быть исправлены.
Из-за необходимости дополнительных 8-битных избыточных битов четности количество частиц в памяти ECC больше, чем в обычной памяти. Для памяти 1R * 8 памяти ECC требуется 9 частиц. Для памяти 1R*4, поскольку разрядность одной частицы памяти равна 4, необходимы еще две частицы.
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
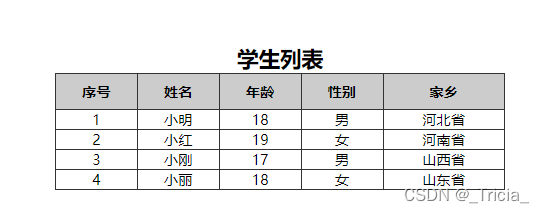
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
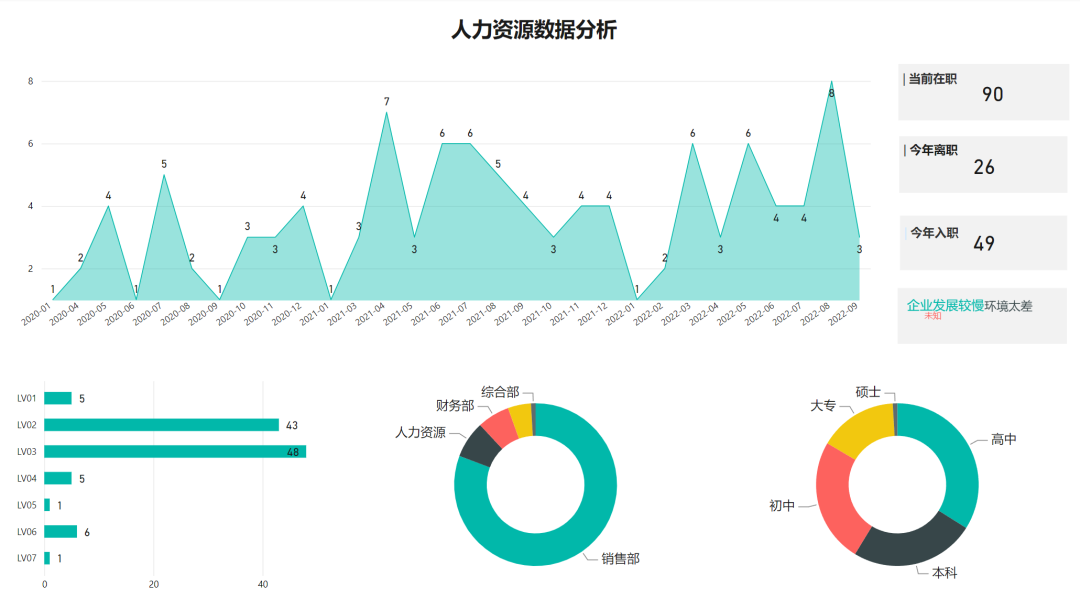
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
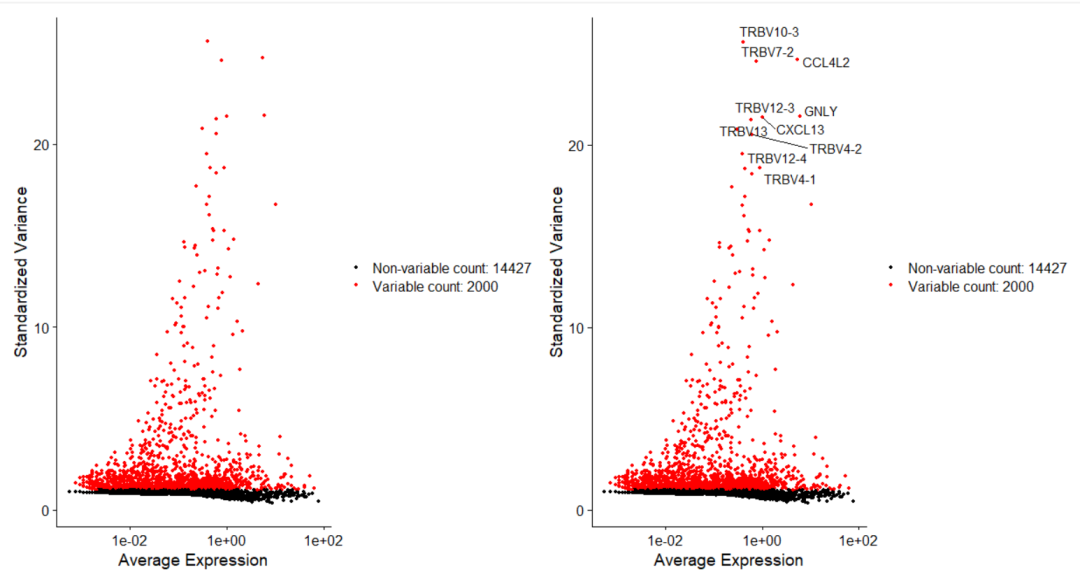
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
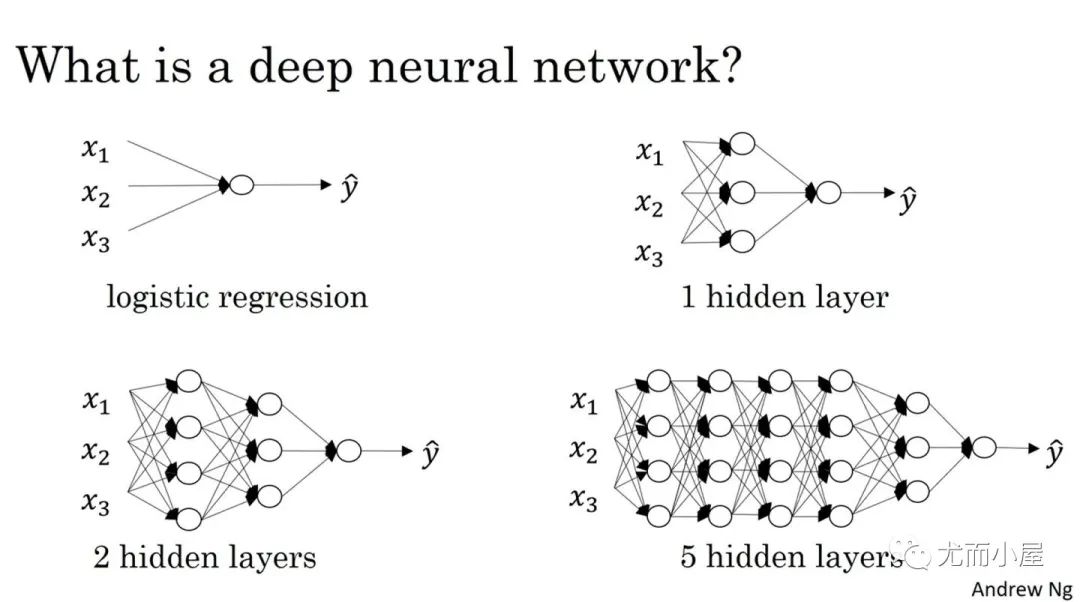
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


