Как дерево Меркла в технологии блокчейна оптимизирует протокол Gossip?
Привет всем, я программист.
Если вы изучали кластер Redis, то знаете, что кластер Redis передает сообщения через протокол Gossip, а сам Gossip имеет множество недостатков.
Поэтому в этой статье мы расскажем, что такое протокол Gossip и как оптимизировать протокол Gossip на основе деревьев Меркеля.
Во многих статьях сейчас говорится, что сплетни — это механизм распространения слухов. На самом деле это слух сам по себе. Мы ищем ответы непосредственно в соответствующих статьях.
https://bitsavers.trailing-edge.com/pdf/xerox/parc/techReports/CSL-89-1_Epidemic_Algorithms_for_Replication_Database_Maintenance.pdf Ссылка на сплетни
В статье Gossip упоминаются три метода распространения сообщений:
Прямая почтовая рассылка Mail):всякий раз, когда происходит обновление,Обновления немедленно рассылаются на все остальные сайты с того сайта, на котором они появляются. Этот подход является своевременным и относительно эффективным.,Однако электронное письмо может быть потеряно или у отправителя может быть неполная информация о других сайтах.,Надежность недостаточная.

Антиэнтропия):Каждый сайт случайным образом периодически выбирает другой сайт.,И устраните различия между ними путем обмена содержимым библиотеки данных. Антиэнтропийный механизм очень надежен.,Потому что это гарантирует, что данные в конечном итоге будут единообразными на всех сайтах.,Но из-за необходимости сравнения всего содержимого библиотеки данных,Частое использование потребляет много ресурсов.

Распространение слухов (слух Mongering):Когда сайт получает новые обновления,Обновление считается «горячим слухом». Сайты, распространяющие острые слухи, регулярно случайным образом выбирают другие сайты.,Убедитесь, что эти сайты также видят обновление. Когда сайт пытается поделиться информацией со слишком большим количеством сайтов, которые уже знают об обновлении.,Это прекратит распространение этого слуха. Слухи распространяются чаще, чем антиэнтропия,Потому что это требует меньше ресурсов,Однако возможно, что обновления могут дойти не до всех сайтов.

[Это также причина, по которой в некоторых статьях в Интернете говорится, что протокол сплетен не будет повторно отправлять сообщения на один и тот же узел, а некоторые говорят, что он будет отправлять сообщения на один и тот же узел. Потому что сообщения, которые не будут повторно отправляться на один и тот же узел, являются антиэнтропийными механизмами, а сообщения, которые будут неоднократно отправляться на один и тот же узел, являются механизмами распространения слухов. Оба эти механизма относятся к механизму передачи сообщений протокола Gossip. В этой статье мы в основном говорим о способах распространения слухов. ]
Протокол Gossip в кластере Redis использует механизм распространения слухов. Протокол Gossip используется для распространения информации о состоянии между различными узлами кластера Redis. Каждый узел периодически обменивается информацией с другими узлами, включая состояние работоспособности узла, отношения главный-подчиненный осколков данных и т. д. Этот механизм гарантирует, что все узлы смогут своевременно понимать изменения состояния всего кластера.
Общим механизмом работы протокола Gossip в кластере Redis является механизм PingPang:

В этом процессе, поскольку количество узлов в кластере Redis продолжает увеличиваться, объем информации, передаваемой протоколом Gossip, продолжает увеличиваться. Предполагая, что у нас есть N узлов, нам нужно постоянно отправлять импульсы N-1 узлам, чтобы доказать, что мы живы. И каждый такт должен переносить информацию о N/10 узлах.
[Что касается того, почему каждый тактовый сигнал несет информацию о N/10 узлах вместо N-1 узла, автор фактически объясняет это в исходном коде:

О чем говорит Джилигуулу? Вкратце, автор имеет в виду, что все узлы являются главными узлами. Выбор соотношения 1/10 может гарантировать, что в большинстве случаев (в частности, 80%), даже если имеется несколько главных узлов. узлы Даже если узлы выходят из строя одновременно, информация о неисправности может эффективно распространяться. ]
Но даже если мы сократим количество сообщений, передаваемых каждым тактовым сигналом, по мере увеличения количества узлов кластера Redis все равно придется передавать огромные объемы данных в режиме pingpang.
Тогда давайте подумаем: если это не работает, не передавайте большие объемы данных в ежедневном PingPang, а измените их на хеширование. Существует большая вероятность того, что хэш-значения двух разных данных будут разными (могут существовать конфликты хеш-функций).
Основываясь на этой идее, мы можем сначала передать хэш-значение данных. Когда хеш-значения двух данных различны, реальные данные передаются для синхронизации данных между двумя узлами.
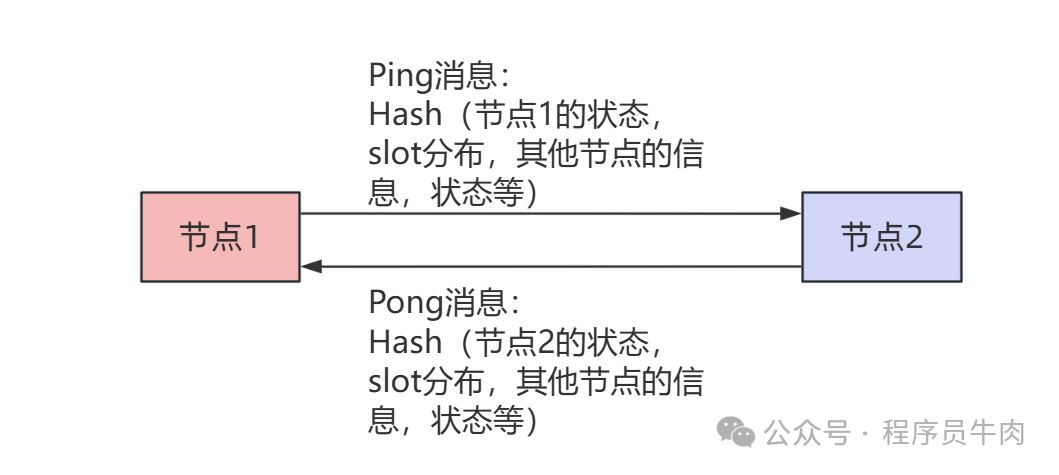
Первая версия плана уже доступна. Можем ли мы подумать о том, как его оптимизировать?
С этим текущим решением все еще существует проблема: когда хэш-значения двух узлов различны, узлы должны обновить все данные. Но в большинстве случаев большая часть информации двух узлов может быть одинаковой, но одно изменилось.
Это просто. Он передается блоками. Нам нужно только сравнить блоки данных. Если какой-либо блок данных отличается, мы можем просто изменить этот блок.
Что касается репликации предыдущей идеи, то на самом деле эти разделенные блоки не нужно передавать. Просто передайте хеш-данные, соответствующие этому блоку.
В этом процессе мы использовали дерево Меркеля для быстрой проверки целостности и согласованности данных.
[Сущность дерева Меркеля — это хеш-дерево, и каждый из его узлов хешируется дочерними узлами. На основании этого свойства деревья Меркла часто используются для проверки и извлечения транзакций в технологии блокчейн.
Если вы хотите кратко понять криптовалюту, вы можете прочитать эту статью, которую я написал ранее:
]
Давайте посмотрим на структуру данных дерева Меркла:
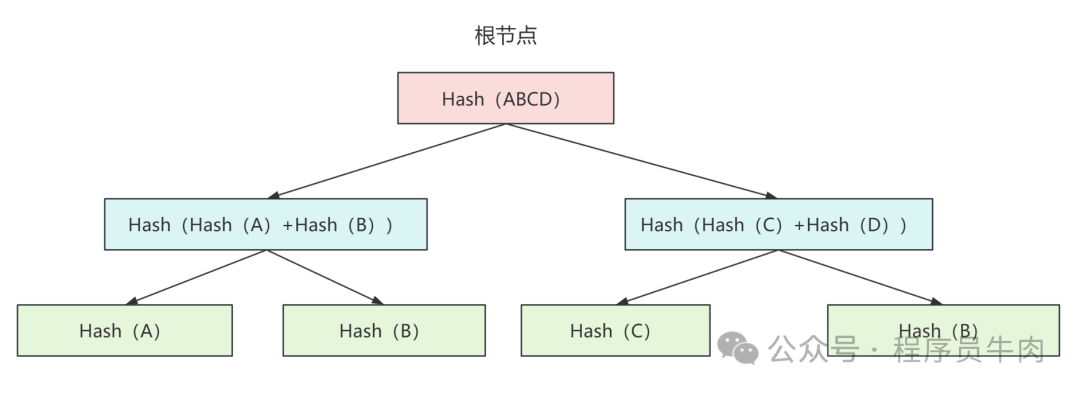
Мы можем понимать подузел ABCD как пакеты данных, которые сегментированы в один и тот же пакет данных. Согласно структуре данных Меркла, любое незначительное изменение в дочерних узлах приведет к изменениям в головном узле.
Таким образом, нам нужно только перенести в сообщение Ping соответствующие хеш-значения этих узлов, указанные на рисунке выше. Например, для 4 пакетов данных мы можем нести 7 хэш-значений. Если эти хэши одинаковы, мы также можем передавать эти хеш-значения в сообщении Pong так же, как сообщение ping. Благодаря этому механизму мы значительно экономим количество сообщений, которые необходимо передать в пинг-понге.
При сравнении вам нужно только сравнить хеш-значения информации четырех узлов. Причина, по которой передается оставшаяся информация об узлах дерева, заключается в том, что можно проверить целостность данных.
[Мы передаем новые данные C и соответствующий корневой узел в сообщении о доставке. После того, как мы заменим данные C целевого дерева, мы можем попытаться хешировать текущий узел дерева полностью, чтобы найти последнее значение корневого узла, и сравнить, совпадает ли переданное значение корневого узла со значением корневого узла, рассчитанным по формуле мы сами. Если хэш-значения двух корневых узлов одинаковы, это означает, что переданный C является полным]
И мы все можем разработать такой план,Это доказывает, что он уже не новый человек.。В МэйтуанеобщественныйЭто внесено в техническую документацию.,Если вам интересно, вы можете взглянуть на этот документ:
https://tech.meituan.com/2024/03/15/kv-squirrel-cellar.html Сопутствующие публичные документы
В этой статье мы кратко представляем их оптимизацию протокола Gossip на основе деревьев Меркла.
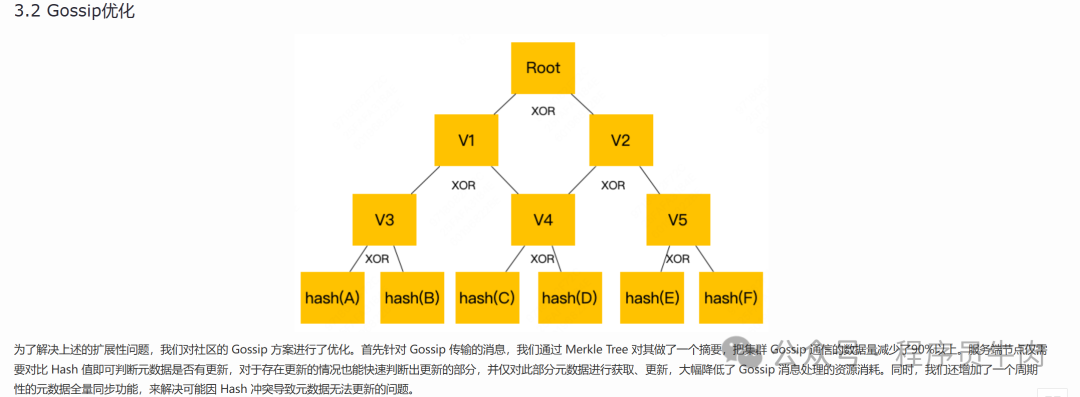
На самом деле, здесь мы можем увидеть нечто более интересное.:они построилиMerkleдерево и нашНе совсем то же самое:
[Их родительский узел использует хеш-значение двух дочерних узлов.исключающее ИЛИполученный,Наша задача — сложить хеш-значения двух узлов и еще раз их хэшировать. ]
В чем разница между ними??Ниже приводитсяЭто всего лишь мое личное предположениеПонятно,Просто веселитесь всем.
Расчет XOR — замечательный расчет, он может рассчитывать и оценивать друг друга. Например, если вы выполните XOR A и B, вы получите C. Тогда вы можете получить A, выполняя XOR C и B, и вы можете получить B, выполняя XOR C и A.
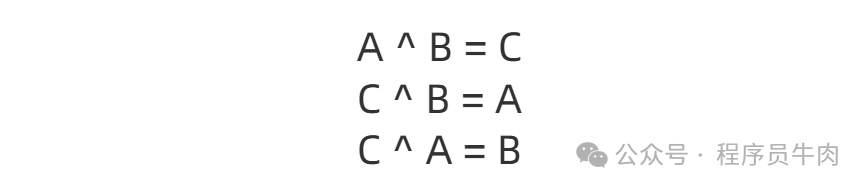
Например, ссылаясь на дерево на рисунке выше, если у нас есть V5 и Хэш (F), мы можем фактически использовать эти два значения для XOR, чтобы вычислить, каким должно быть значение Хэша (E). Это возможность, которой нет в нашем исходном дереве Меркла.
На основе этой операции мы фактически имеем метод проверки сверху вниз по сравнению с исходным деревом Меркла.
На самом деле, такого рода операции очень распространены. Если вы провели анализ «темной лошадки», вы будете использовать структуру данных, называемую фильтром Блума. Фильтры Блума не могут удалять элементы из-за проблем с дизайном. Чтобы улучшить эту ситуацию, мы разработали фильтр с кукушкой.
Хэш-фильтр cuckoo использует хеш-структуру cuckoo. Мы хешируем данные, чтобы получить отпечаток пальца, и помещаем их в эту хеш-структуру с кукушкой.
Для каждого отпечатка пальца предусмотрено два места, чтобы избежать скопления людей. Первая координата вычисляется с помощью хеш-функции, а вторая координата представляет собой операцию XOR с использованием хэша первой координаты и отпечатка пальца. Операция XOR выполняется в соответствии с характеристиками операции XOR: a^ b = c,c. ^ b= a, c^a=b, мы можем быстро передавать данные друг другу.
Другими словами, когда текущие данные в корзине заняты, мы можем напрямую вычислить резервную корзину, используя индекс i текущей корзины и отпечаток пальца, хранящийся в корзине. Если вы не знаете о фильтрах кукушки, вы можете взглянуть на эту статью, которую я написал ранее:
Не знаете, что такое фильтр-кукушка? Вернитесь назад и дождитесь уведомления
На этом заканчивается сегодняшнее введение в то, как дерево Меркла в технологии блокчейна оптимизирует протокол Gossip. На самом деле оно было довольно расплывчатым и давало лишь общее представление.
Поскольку на меня распространяется конфиденциальность компании, я не могу поделиться с вами более подробной информацией по этому поводу. Приглашаем вас присоединиться к Meituan и лично убедиться в том, какие оптимизации мы внесли в этом отношении.
Что вы хотите сказать о деревьях Меркла? Добро пожаловать, чтобы оставить сообщение в области комментариев.
Следуйте за мной, чтобы узнать больше о информатике.
end
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
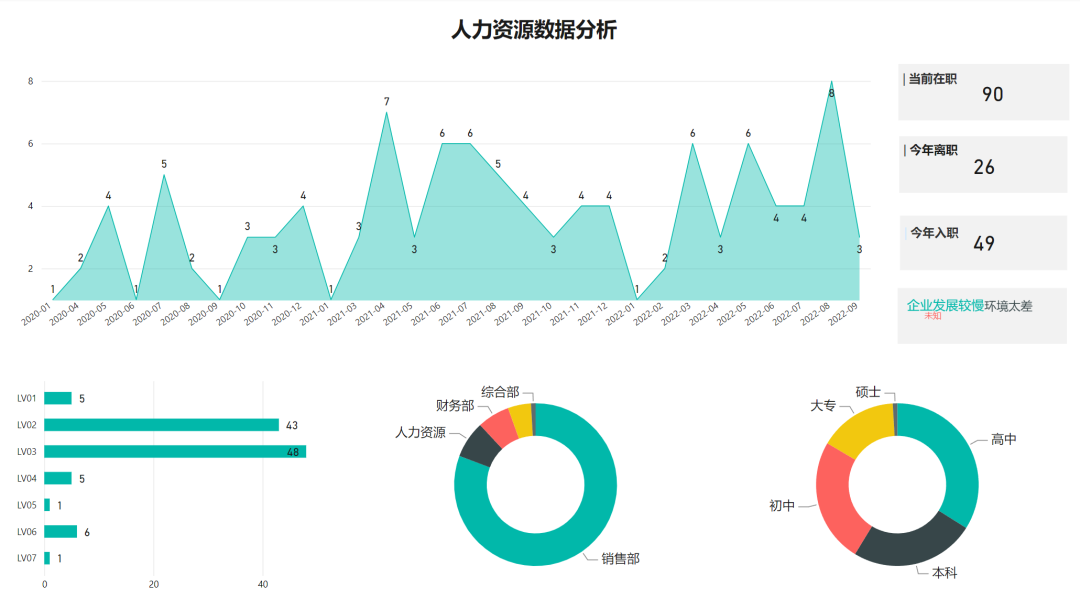
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
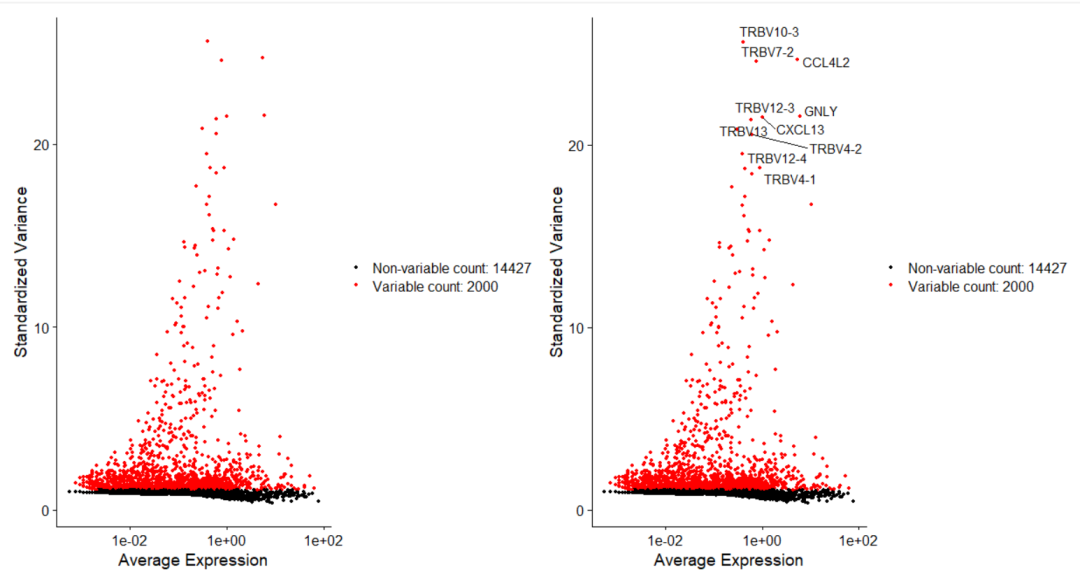
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


