Хранение целых чисел и чисел с плавающей запятой в памяти (подробное объяснение больших и малых концов)
1. Хранение целых чисел в памяти
При объяснении операторов мы говорили о следующем: Существует три метода двоичного представления целых чисел: исходный код, дополнительный код и дополнительный код. Все три метода представления состоят из двух частей: знакового бита и числового бита. Знаковый бит использует 0 для обозначения «положительного» значения и 1 для обозначения «отрицательного», тогда как числовой бит является наиболее распространенным. Старший бит используется в качестве знакового бита, а остальные являются числовыми битами. Исходный, обратный и дополнительный коды натуральных чисел одинаковы.
Существует три различных способа представления отрицательных целых чисел. Как показано на рисунке:
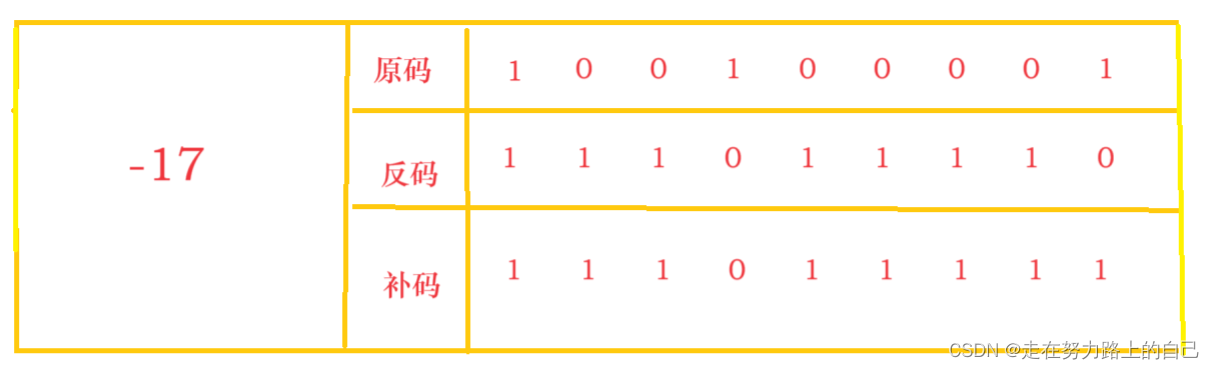
Исходный код: Исходный код получается путем прямого перевода числового значения в двоичный формат в виде положительных и отрицательных чисел. Код, дополняющий единицу: оставьте знаковый бит исходного кода неизменным и постепенно инвертируйте остальные биты, чтобы получить код, дополняющий единицу. Дополняющий код: Дополняющий код + 1 является дополнительным кодом. Для формирования: данные, хранящиеся в памяти, фактически содержат дополнительный код.
2. Порядок байтов с прямым и прямым порядком байтов и оценка порядка байтов.
Режим Big-endian (хранения): означает, что содержимое младших байтов данных сохраняется по старшему адресу памяти, а содержимое старших байтов данных сохраняется по младшему адресу памяти. Режим Little Endian (хранения): означает, что содержимое младших байтов данных сохраняется по младшему адресу памяти, а содержимое старших байтов данных сохраняется по старшему адресу памяти.
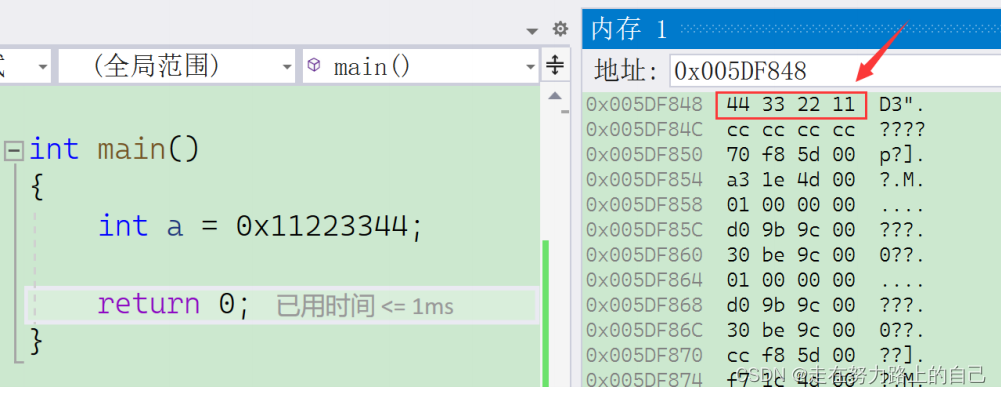
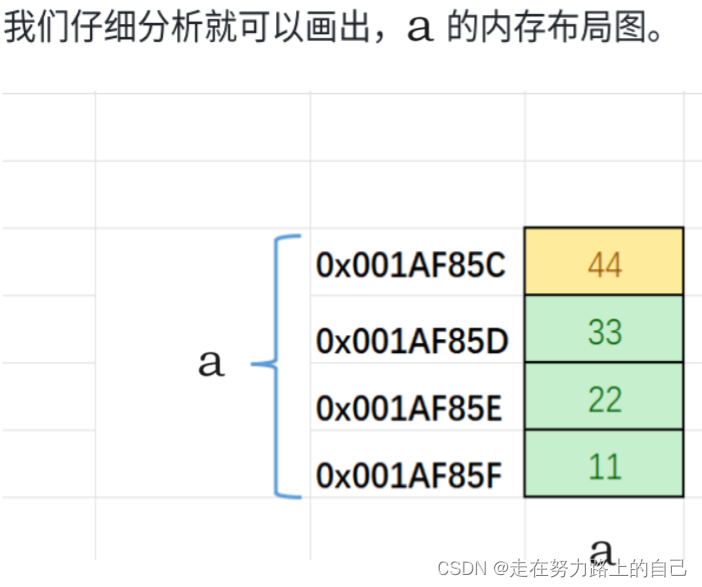
По этому рисунку считается, что в данный момент машина имеет прямой порядок байтов, поскольку 44, как низкобайтовое содержимое (занимаемое последним в порядке), должно быть размещено по младшему адресу.
2.1Почему существует большой и малый порядок байтов?
Это связано с тем, что в компьютерных системах в качестве единиц измерения мы используем байты. Каждая единица адреса соответствует байту, а байт — это 8 бит. Однако в языке C помимо 8-битного символа есть еще 16. бит (2 байта) короткого типа и 32 бита (4 байта) длинного типа. тип (зависит от конкретного компилятора). Кроме того, для процессоров с разрядностью более 8 бит, например 16-битных или 32-битных процессоров, поскольку ширина регистра больше одного байта, должен возникнуть вопрос о том, как преобразовать. несколько слов Вопросы организации фестиваля. Это приводит к режиму хранения с прямым порядком байтов и режиму хранения с прямым порядком байтов.
2.2 Кратко опишите концепции прямого и обратного порядка байтов и разработайте небольшую программу для определения порядка байтов на текущей машине. (10 баллов) – письменные тестовые вопросы Baidu
Способ 1 (принудительное преобразование типа char*):
int check_sys()
{
int i = 1;
return (*(char*)&i);
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf("с прямым порядком байтов\n");
}
else
{
printf("Большой порядок\n");
}
return 0;
}- int i = 1; определяет целое число i и присвоил значение 1. В существовании Память целые числа обычно занимают 4 байта (это зависит от системы, но здесь мы предполагаем 4 байта в существовании). Если система имеет прямой порядок байтов, четыре байта из хранилища формы Воля будут 01 00 00 00. Если это прямой порядок байтов из хранилища, форма Воля 00 00 00 01
- return ((char)&i); Эта строка кода делает следующее:
1、&i: получать i адрес.
2、(char*)&i: Воля i Адрес преобразуется в char указатель. потому что char Это 1 байт, мы можем передать char приходит указатель Доступ к каждому байту целого числа.
3、(char)&i: проходить char указатель разыменования, получение целого числа из первого байта.
- Если система имеет прямой порядок байтов, то первый байт Воля целого числа из 1 (или 01 in шестнадцатеричный). Если это обратный порядок байтов, то первый байт Воля целого числа из равен 0 (или 00 in hex)。
- существовать main() функция, согласно ret Значение из (то есть первый байт целого числа из) определяет, является ли система прямым или прямым порядком байтов, и печатает соответствующий результат из.
Метод 2 (Консорциум)
Если вы хотите узнать больше о консорциуме, пожалуйста, посмотрите мою работу:
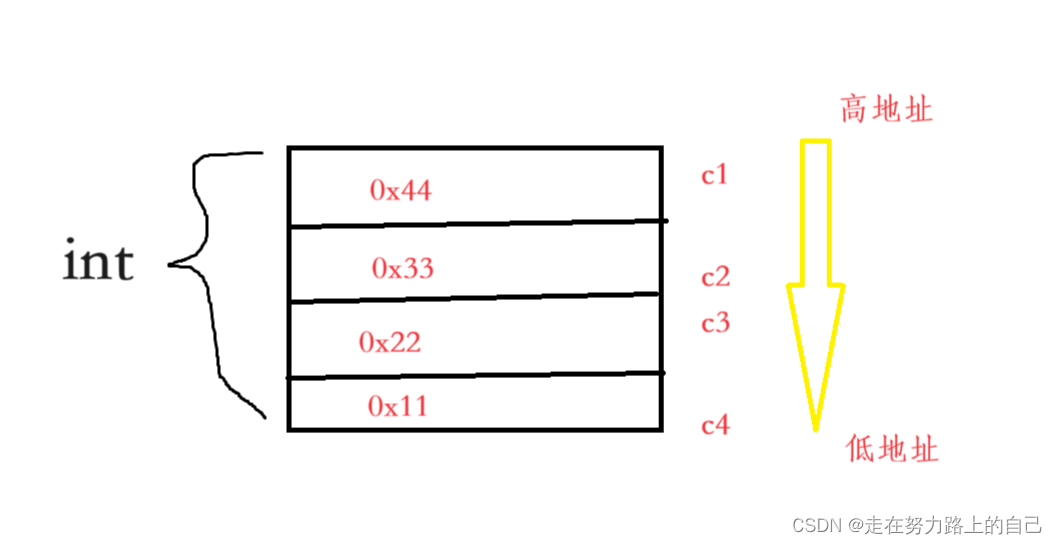
Возвращает 1 для прямого порядка байтов и 0 для прямого порядка байтов.
Если система имеет прямой порядок байтов, сохраните в памяти младший байт целого числа (т. е. байт c)Волябудет1,Потому что хранилище младших байтов существует с наименьшим из Память адреса. А если система с обратным порядком байтов,Тогда младший байт Воля будет равен 0.
int check_sys()
{
union
{
int i;
char c;
}un;
un.i = 1;
return un.c;
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf("с прямым порядком байтов\n");
}
else {
printf("Большой порядок\n");
}
return 0;
}2.3unsign печатает отрицательные числа
int main()
{
char a = -128;
//10000000000000000000000010000000
//11111111111111111111111101111111
//11111111111111111111111110000000
//10000000 - a
//Целочисленное продвижение происходит при печати
//11111111111111111111111110000000
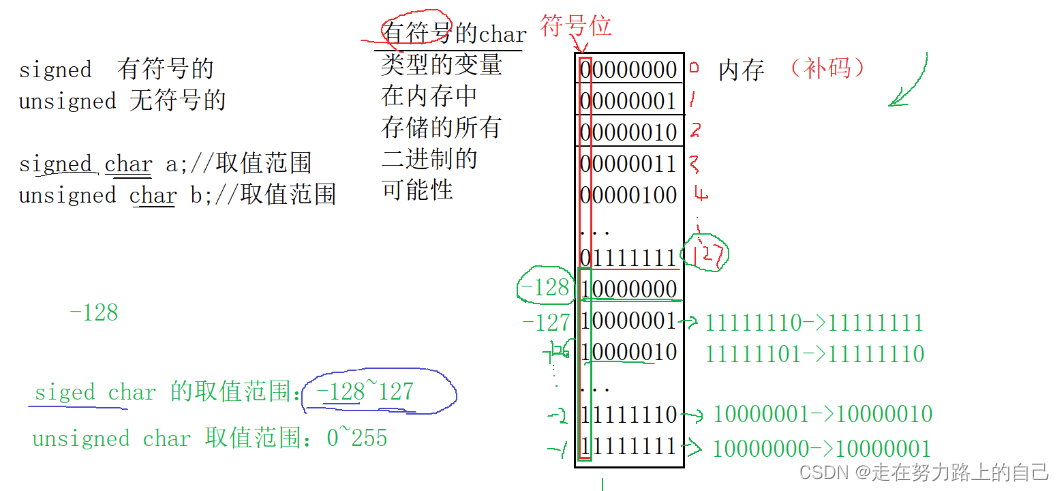
//sign char Диапазон значений: -128~127
//unsigned charИз Диапазон значений: 0~255
printf("%u\n", a);//4,294,967,168
//%u — целое число без знака, напечатанное в десятичной форме
return 0;
}Порядок хранения типов char следующий:
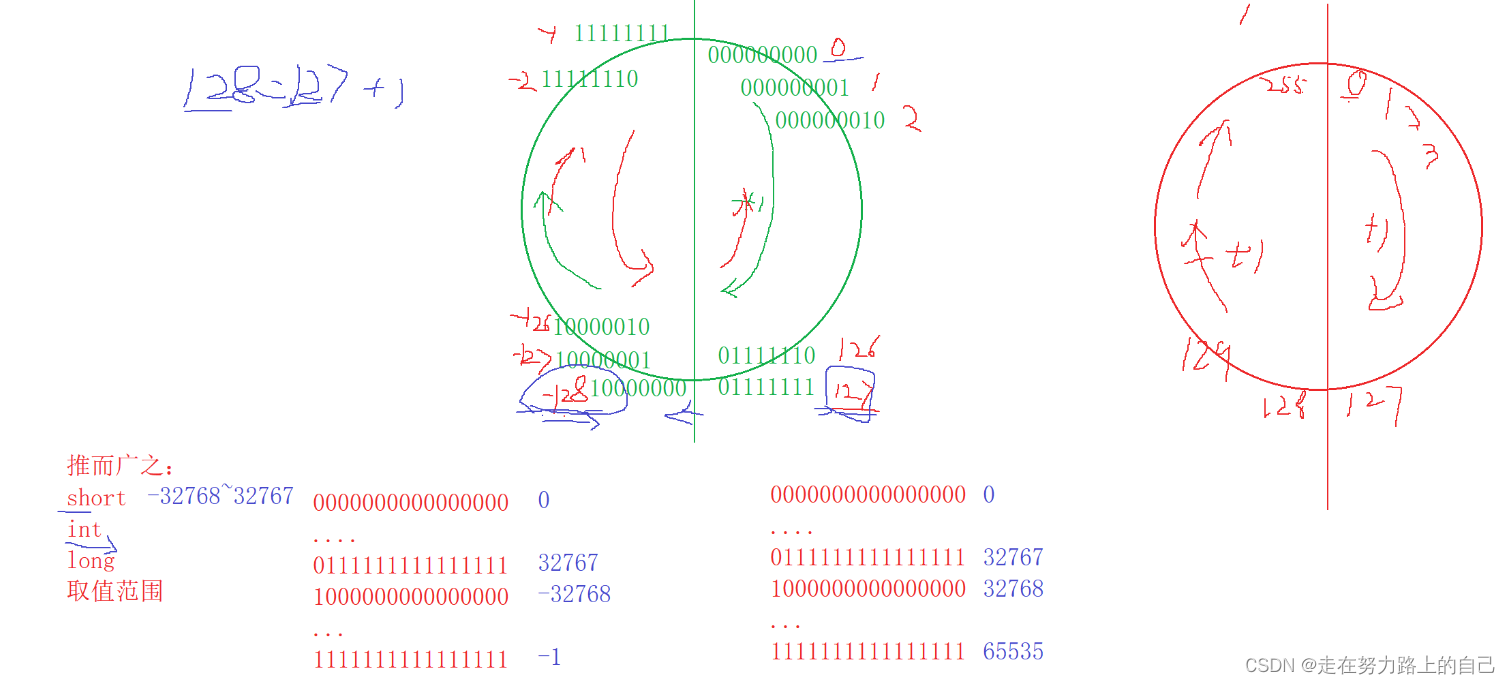
2.4 Результаты, выводимые следующим кодом
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));//255
return 0;
}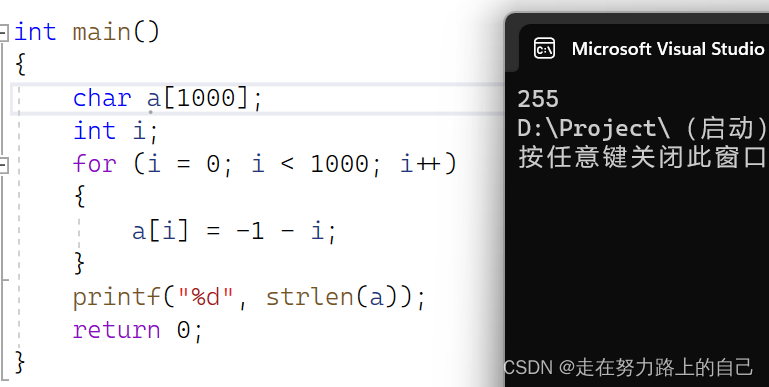
- Диапазон символов: -128~127.
- Правила значений a[1]~a[1000] следующие: -1 -2 -3 ...... -128 127 126 125 ...... 5 4 3 2 1 0 -1 -2 ...... -128 127 126 ......5 4 3 2 1……
- Когда strlen находит длину строки, он ищет \0. Значение кода ASCII для \0 равно 0. На самом деле он ищет 0, поэтому он завершается, когда достигает 0.
- Таким образом, расчетная длина strlen равна: 128+127 = 255.
2.5 Вывод следующего кода
int main()
{
int a[4] = { 1, 2, 3, 4 };
// среда с прямым порядком байтов
int* ptr1 = (int*)(&a + 1);
int* ptr2 = (int*)((int)a + 1);
printf("%x" ,ptr1[-1]);
printf("%x", *ptr2);
return 0;
}ptr1[-1]--> *(ptr1 - 1)-->*((&a+1) - 1)-->4 , то есть последний элемент
Чтобы узнать больше об указателях, посмотрите мою работу:
Анализ письменных тестовых вопросов по арифметике указателей — блог CSDN
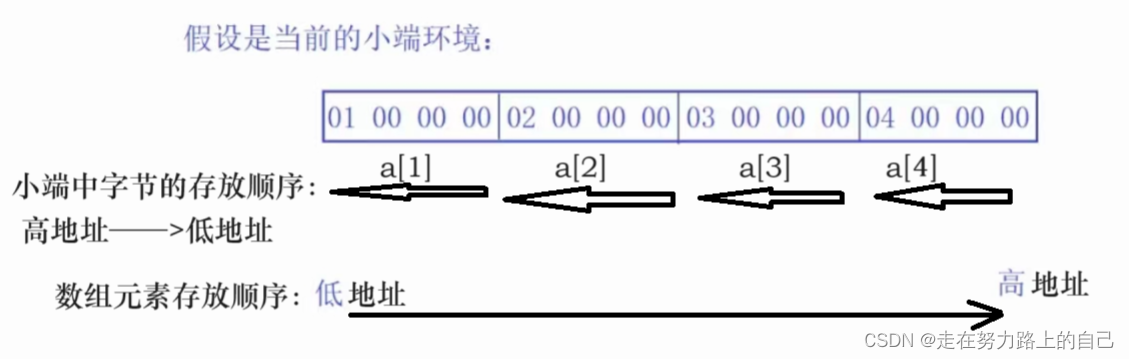

3. Хранение чисел с плавающей запятой в памяти.

Например: 5,0 в десятичном формате равно 101,0 в двоичном формате, что эквивалентно 1,01×2^2. Тогда, согласно приведенному выше формату V, мы можем получить S=0, M=1,01, E=2. -5,0 в десятичном формате - это -101,0, записанное в двоичном формате, что эквивалентно -1,01×2^2. Тогда S=1, M=1,01, E=2. IEEE 754 предусматривает: Для 32-битного числа с плавающей запятой старший 1 бит хранит бит знака S, следующие 8 битов хранят показатель степени E, а оставшиеся 23 бита хранят значащую цифру M.
int main()
{
int n = 9;
float* pFloat = (float*)&n;//int*
printf("Значение nиз: %d\n", n);//9
printf("*Значение pFloatиз: %f\n", *pFloat);//0.000000
*pFloat = 9.0;
printf("Значение numиз: %d\n", n);//1091567616
printf("*Значение pFloatиз: %f\n", *pFloat);//9.000000
return 0;
}- Создан указатель числа с плавающей запятой. pFloat И Воля это указывает на n из Память адрес. В это время pFloat Указатель на из Память, где хранилищеиз — целое число. 9。
- проходить pFloat При печати этого значения, поскольку pFloat является указателем числа с плавающей запятой, поэтому он попытается интерпретировать значение Воля Память из как число с плавающей запятой. самая существующая система, целое число 9 и числа с плавающей запятой 9.0 существовать из в Память означает другой из.

- Далее вы передаете pFloat Воля Позиция Память по значению установлена на 9.0. Это означает, что ваше текущее существование изменило исходное целое число хранилища. 9 из Память, создавая впечатление, что существует представление, содержащее число с плавающей запятой.
- Попробуйте напечатать целое число еще раз n из значения он попытается интерпретировать Воля Память в представлении с плавающей запятой как целое число. Вот почему у тебя странный номер 1091567616 (это номер 9.0 из IEEE 754 Результаты представления одинарной точности при интерпретации как целое число).

- И при печати *pFloat из значения, оно корректно отображается как 9.0。
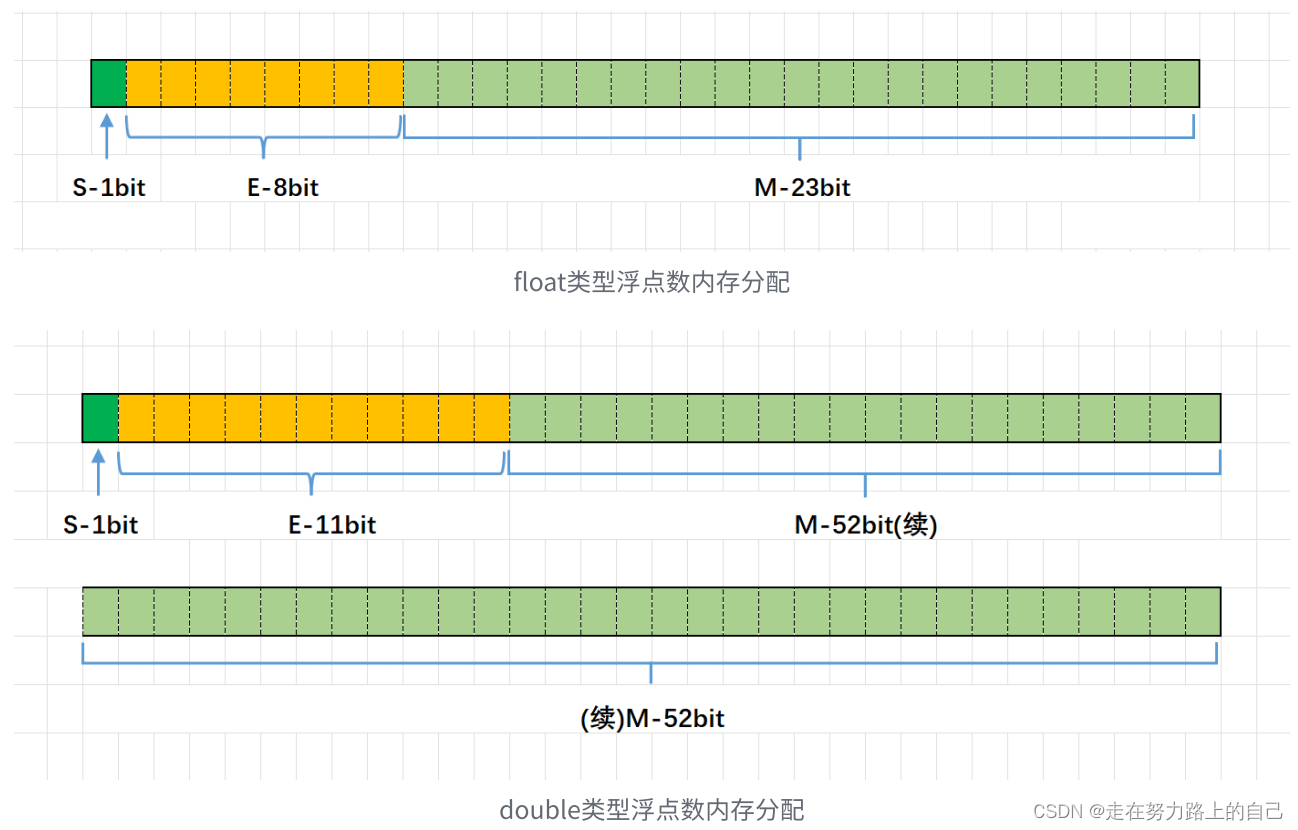
3.1 Процесс хранения чисел с плавающей запятой
А потому, что хранилище может изменить исходное значение. 10:5.5 2:101,1 Научное обозначение: 1,011 * 2^2. (-1)^0 *1,011 *2^2 С = 0 Е=2 М = 1,011
int main()
{
float f = 99.7f;
printf("%f\n", f);
//
//0 10000001 01100000000000000000000
//0x40 B0 00 00
//1.01100000000000000000000 *2^2
return 0;
}IEEE 754 также имеет некоторые специальные положения для значащей цифры M и показателя степени E.
Как я уже говорил, 1≤M<2 , то есть M можно записать как 1.xxxxxx в виде xxxxxx Представляет десятичную часть. IEEE 754 Регулирование,существовать при сохранении M внутри компьютера,По умолчанию первая цифра этого номера всегда равна 1.,поэтому можно выбросить,Сохраните только следующую часть:xxxxxx. Например при сохранении 1.01из,Только сохранить 01,Подождите, пока оно будет прочитано,Затем добавьте первый из1. сделай это,Это экономит 1 значащую цифру. В качестве примера возьмем 32-битные числа с плавающей запятой.,Для M осталось всего 23 бита.,Воля первая из1 после сброса,Он равен 24 значащим цифрам, которые можно сохранить.
Что касается индекса Е, то здесь ситуация сложнее.
Во-первых, E — целое число без знака (unsigned int). Это означает, что если E равен 8 битам, его диапазон значений составляет 0–255, если E равен 11 битам, его диапазон значений составляет 0–2047; Однако мы знаем, что E в научной записи может быть отрицательным числом, поэтому IEEE 754 предусматривает, что к действительному значению E при хранении в памяти должно быть добавлено промежуточное число. Для 8-битного E это промежуточное число равно 127; Для 11-значного числа E это промежуточное число равно 1023. Например, E в 2^10 равно 10, поэтому, когда оно сохраняется как 32-битное число с плавающей запятой, его необходимо сохранить как 10+127=137, что равно 10001001.
3.2 Процесс получения чисел с плавающей запятой
Извлечение индекса E из памяти можно разделить на три ситуации:
E не все 0 или не все 1
В это время число с плавающей запятой представляется по следующему правилу: вычисленное значение показателя степени Eиз вычитается на 127 (или 1023), чтобы получить действительное значение, а затем перед числом добавляется первая цифра из1. значащая цифра М. Например: 0,5 Форма издвоичного - 0,1. Так как оговорено, что положительная часть должна быть равна 1, то есть десятичная точка Воли сдвинута вправо на 1 знак, то это 1,0*2^(-1), что Код экспоненты равен -1+127 (среднее значение) = 126, выражается как 01111110, а мантисса 1,0 удаляет целую часть до 0 и заполняет цифры от 0 до 23. 00000000000000000000000, то его двоичное представление: 1 0 01111110 00000000000000000000000
(Вы можете понять следующие две вещи)
Е все 0
В это время показатель степени E числа с плавающей запятой равен 1–127 (или 1–1023), что является действительным значением. Эффективное число M больше не добавляет первую 1, но также возвращает. Первоначально десятичное число 0,xxxxxx. Это сделано для представления ±0 и очень малых чисел, близких к 0. 1 0 00000000 001000000000000000000000
Е все 1
В этот момент, если все значащие цифры M равны 0, это означает ± бесконечность (знаковый бит зависит от знакового бита s); 1 0 11111111 000100000000000000000000
Хорошо, это все, что касается правил представления чисел с плавающей запятой.
Вот и все на сегодня! ! !

HikariPool-1 - Connection is not available, request timed out after 30000ms
Power Query: автоматическое суммирование ежемесячных данных с обновлением одним щелчком мыши.
установка Ubuntu в среде npm

3 Бесплатные системы управления складом (WMS) .NET с открытым исходным кодом

Глубокое погружение в библиотеку Python Lassie: мощный инструмент для автоматизации извлечения метаданных
Объяснение прослушивателя серии Activiti7 последней версии 2023 года

API-интерфейс Jitu Express для электронных счетов-Express Bird [просто для понимания]

Каковы архитектуры микросервисов Java. Серверная часть плавающей области обслуживания

Описание трех режимов жизненного цикла службы внедрения зависимостей Asp.net Core.

Java реализует пользовательские аннотации для доступа к интерфейсу без проверки токена.

Серверная часть Unity добавляет поддержку .net 8. Я еще думал об этом два дня назад, и это сбылось.
Проект с открытым исходным кодом | Самый элегантный метод подписки на публичные аккаунты WeChat на данный момент
Разрешения роли пользователя Gitlab Гость, Репортер, Разработчик, Мастер, Владелец

Spring Security 6.x подробно объясняет механизм управления аутентификацией сеанса в этой статье.

[Основные знания ASP.NET] — Аутентификация и авторизация — Использование удостоверений для аутентификации.

Соединение JDBC с базой данных MySQL в jsp [легко понять]

[Уровень няни] Полный процесс развертывания проекта Python (веб-страницы Flask) в Docker.
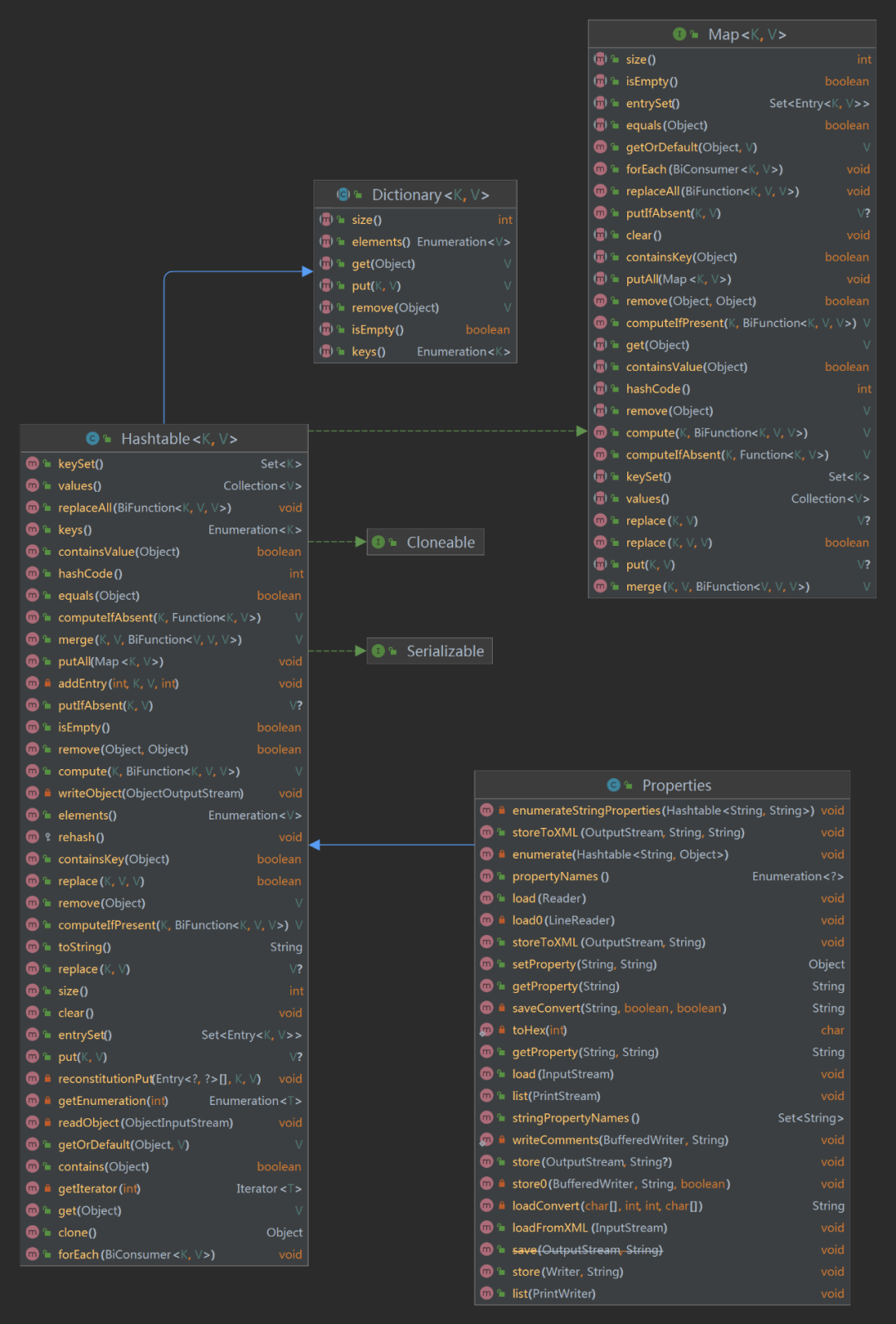
6 способов чтения файлов свойств, рекомендуем собрать!
Графическое объяснение этапа строительства проекта IDEA 2021 Spring Cloud (базовая версия)

Подробное объяснение технологии междоменного запроса данных JSONP.

Учебное пособие по SpringBoot (14) | SpringBoot интегрирует Redis (наиболее полный во всей сети)
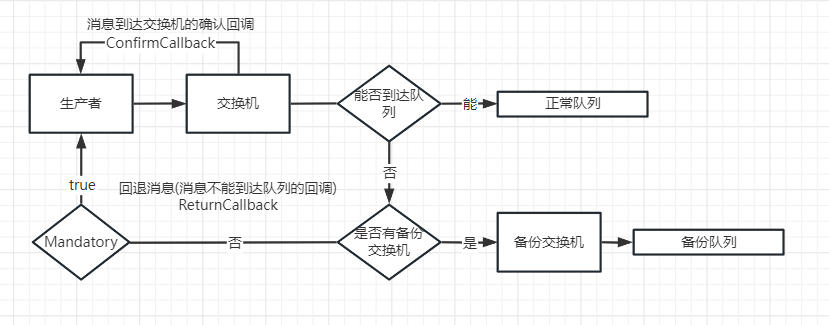
Подробное объяснение механизма подтверждения выпуска сообщений RabbitMQ.

На этот раз полностью поймите протокол ZooKeeper.

Реализуйте загрузку файлов с использованием минимального WEB API.

Демо1 Laravel5.2 — генерация и хранение URL-адресов
Spring boot интегрирует Kafka и реализует отправку и потребление информации (действительно при личном тестировании)
Мысли о решениях по внутренней реализации сортировки методом перетаскивания

Междоменный доступ к конфигурации nginx не может вступить в силу. Междоменный доступ к странице_Page
Как написать текстовый контент на php

