Характеристики распространения сигнала Bellhop в условиях волнистого рельефа морского дна
Характеристики распространения сигнала Bellhop в условиях волнистого рельефа морского дна

Предисловие

В связи с необходимостью выполнения большого задания по курсу подводного акустического канала данный раздел посвящен изучению характеристик распространения звука в волнистых условиях рельефа морского дна.

1. Подготовительный контент

Во всех примерах мы используем глубоководный профиль скорости звука Мунка, который находится в диапазоне от 0 до 5000 м, частота источника звука 50 Гц, расположен на глубине 1000 м, расстояние шага звуковых лучей 100 м, звуковые лучи 70 , сектор угла выхода -13°~ 13°, скорость звука на морском дне 1600 м/с, плотность морского дна 1,8 г/см3, коэффициент затухания на морском дне 0,8. д Б/λ, морская среда показана на рисунке ниже:

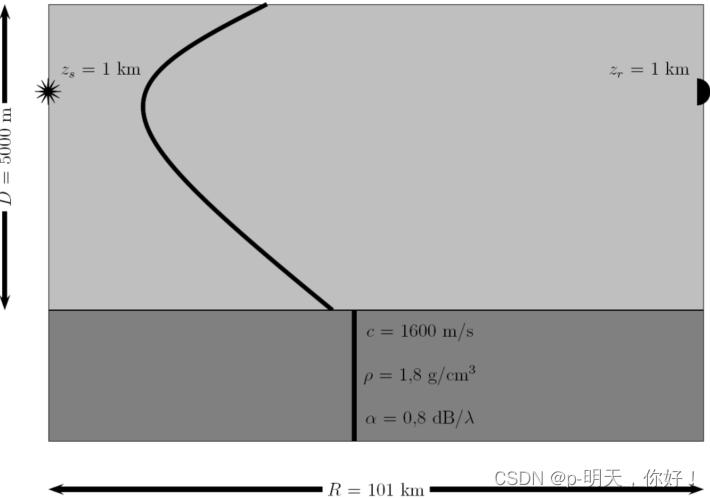
Принципиальная схема глубоководной сцены приложения

2. Горизонтальный подводный волновод (горизонтальное дно).

Примечание. Значение волновода: Океанский волновод можно понимать как канал распространения звуковых волн в океане. Например, в классическом глубоководном профиле Мунка звуковые волны будут ограничены определенным диапазоном каналов и распространяются на большие расстояния. Этот канал можно понимать как океанский волновод.

Начнем с простой акустической траектории (расчета) от 0 до 101 км.

Ниже Matlab код,нарисовано отдельноТраектории звуковых лучей в глубоководных волноводах на уровне морского дна、Собственные звуковые лучи в глубоководных волноводах на уровне морского дна、Потери когерентного распространения в глубоководных волноводах на уровне морского дна、Прибытие звукового луча (импульсная характеристика)

код Язык:javascript
копировать
clc;    clear;  close all;
global units;	units = 'km';
bellhop flatwav_R   %   Runtype = 'R'
figure; plotray flatwav_R	% Горизонтальный луч звука морского дна в глубоководном волноводе
bellhop flatwav_E   %   Runtype = 'E'
figure; plotray flatwav_E	% Собственные звуковые лучи в глубоководных волноводах на уровне морского дна
bellhop flatwav_C   %   Runtype = 'C'
figure; plotshd flatwav_C.shd	% Потери когерентного распространения в глубоководных волноводах на уровне морского дна
bellhop flatwav_A   %   Runtype = 'A'
% [ Arr, Pos ] = read_arrivals_asc( ARRFile, Narrmx )
[ Arr, Pos ] = read_arrivals_asc( 'flatwav_A.arr' );
% plotarr( filename, irr, ird, isd )
plotarr(  'flatwav_A.arr', 1, 1, 1 )	% приезжать из импульсной характеристики на приемнике

Далее мы объясним приведенный выше код отдельно.

1. Звуковые лучи в глубоководных волноводах на уровне морского дна.

①.Файлы среды.

Подробное описание файлов среды можно найти в моем предыдущем блоге.-> Bellhop От начала к началу

flatwav_R.env

код Язык:javascript
копировать
'Munk profile/Flat waveguide/Ray trace'  	% TITLE
50.0 										% FREQ (Hz)
1											% NMEDIA
'SVW'										% SSP-TOP-WATER-OPT
51 0.0 5000.0								% NMESH SIGMA Z(NSSP)
0.0 1548.52 /								% Z() CP() CS() RHO() AP() AS()
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A' 0.0										% BOTOPT SIGMA
5000.0 1600.00 0.0 1.8 .8 0.0				% ZB CPB CSB RHOB APB ASB
1 											% NSD
1000.0 /									% SD(1:NSD) (m)
1 											% NRD
1000.0 /									% RD(1:NRD) (m)
1 											% NRR
101.0 /										% RR(1:NRR ) (km)
'R'											% OPTION: 'R/E/C/A/I/S
70 											% NBEAMS ISINGLE
-13.0 13.0 /								% ALPHA(1:NBEAMS) (°)
100.0 5500.0 102.0							% STEP (m) ZBOX (m) RBOX (km)

②.Команда Matlab

код Язык:javascript
копировать
bellhop flatwav_R   %   Runtype = 'R'
figure; plotray flatwav_R	% Горизонтальный луч звука морского дна в глубоководном волноводе

Как только Bellhop завершит расчет, вы можете проверить, созданы ли два файла: первый — Flatwav_R.prt, содержащий исчерпывающую информацию о характеристиках волновода, количестве углов выхода, времени расчета и т. д., второй — Flatwav_R.ray, который содержит файл координат ASCII-кода лучей, а M-файлplotray.m можно использовать для построения графика.

③、Результаты выполнения

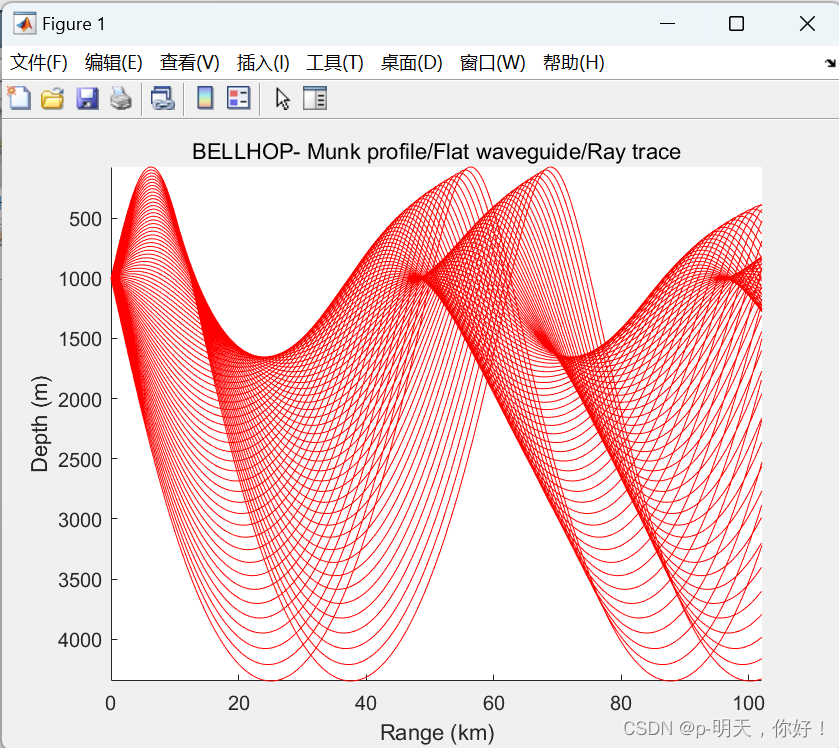
Траектории звуковых лучей в глубоководных волноводах на уровне морского дна

2. Собственные звуковые лучи в глубоководных волноводах на уровне морского дна.

Измените OPTIONS3(1) = «R» на OPTIONS3(1) = «E» и запустите программу, как и раньше, чтобы получить лучи собственного звука.

①.Файлы среды.

Просто измените «R» в строке 41 файла Flatwav_R.env выше на «E».

код Язык:javascript
копировать
'Munk profile/Flat waveguide/Eigenrays'
50.0
1
'SVW'
51 0.0 5000.0
0.0 1548.52 /
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A' 0.0
5000.0 1600.00 0.0 1.8 .8 0.0
1 
1000.0 /
1 
1000.0 /
1 
101.0 /
'E'
70 
-13.0 13.0 /
100.0 5500.0 102.0

②.Команда Matlab

код Язык:javascript
копировать
bellhop flatwav_E   %   Runtype = 'E'
figure; plotray flatwav_E

③、Результаты выполнения

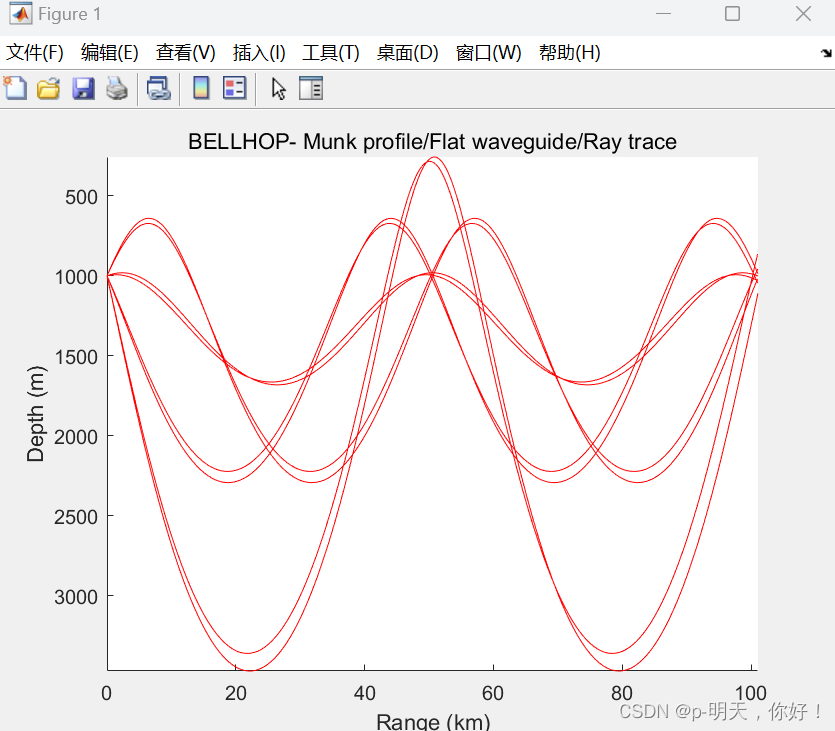
Собственные звуковые лучи в глубоководных волноводах на уровне морского дна

3. Потери когерентного распространения в глубоководных волноводах на уровне морского дна.

Расчет потерь когерентного распространения требует небольшой модификации входного файла. Во-первых, установите OPTIONS3(1) = «C», во-вторых, учтите, что потери при распространении рассчитываются на прямоугольной сетке «расстояние-глубина» размером 501×501 точка; Наконец, мы устанавливаем nbeams = 0 и позволяем Bellhop самостоятельно решать, сколько лучей необходимо.

①.Файлы среды.

flatwav_C.env

код Язык:javascript
копировать
'Munk profile/Flat waveguide/Coherent transmission loss'
50.0
1
'SVW'
51 0.0 5000.0
0.0 1548.52 /
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A' 0.0
5000.0 1600.00 0.0 1.8 .0 .0 /
1
1000.0 /
501
0.0 5000.0 /
501
0.0 101.0 /
'C'
0
-14.0 14.0 /
100.0 5500.0 102.0

②.Команда Matlab

код Язык:javascript
копировать
bellhop flatwav_C   %   Runtype = 'C'
figure; plotshd flatwav_C.shd

Запустив Bellhop, мы получаем двоичный файл с именем Flatwav_C.shd, который фактически содержит последовательно рассчитанное звуковое давление. Мы используем M-файлploshd.m для построения графика потерь при распространении.

③、Результаты выполнения

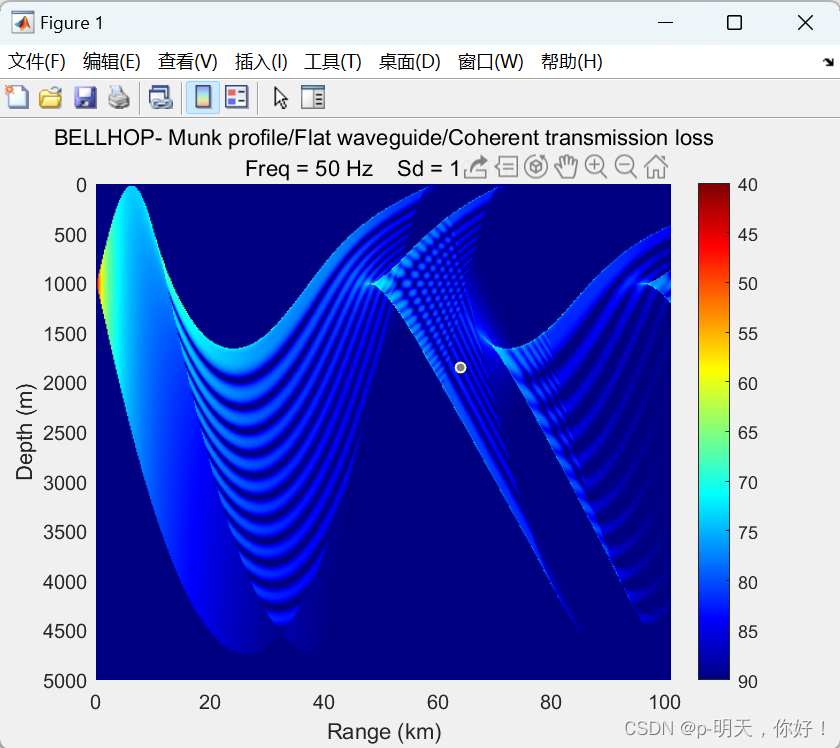
Потери когерентного распространения в глубоководных волноводах на уровне морского дна

4. Импульсный отклик, поступающий в приемник

Измените Flatwav_C.env, чтобы установить OPTIONS3(1)=’A’.

①.Файлы среды.

flatwav_A.env

код Язык:javascript
копировать
'Munk profile/Flat waveguide/Arrive'
50.0
1
'SVW'
51 0.0 5000.0
0.0 1548.52 /
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A' 0.0
5000.0 1600.00 0.0 1.8 .0 .0 /
1
1000.0 /
1
1000.0 /
1
101.0 /
'A'
101
-14.0 14.0 /
100.0 5500.0 102.0

②.Команда Matlab

код Язык:javascript
копировать
bellhop flatwav_A   %   Runtype = 'A'
% [ Arr, Pos ] = read_arrivals_asc( ARRFile, Narrmx )
[ Arr, Pos ] = read_arrivals_asc( 'flatwav_A.arr' );
% plotarr( filename, irr, ird, isd )
plotarr(  'flatwav_A.arr', 1, 1, 1 )

После запуска Bellhop вы получаете файл ascii-кода с именем Flatwav_A.arr, который содержит амплитуду и время прохождения лучей, приходящих в местоположение приемника (мы ссылаемся только на одну точку местоположения, модель способна рассчитать звуковые лучи, приходящие в все точки массива во времени и амплитуде распространения блока массива). Данные, содержащиеся в файлах *.arr, можно прочитать с помощью M-файла read_arrivals_asc.m.

③、Результаты выполнения

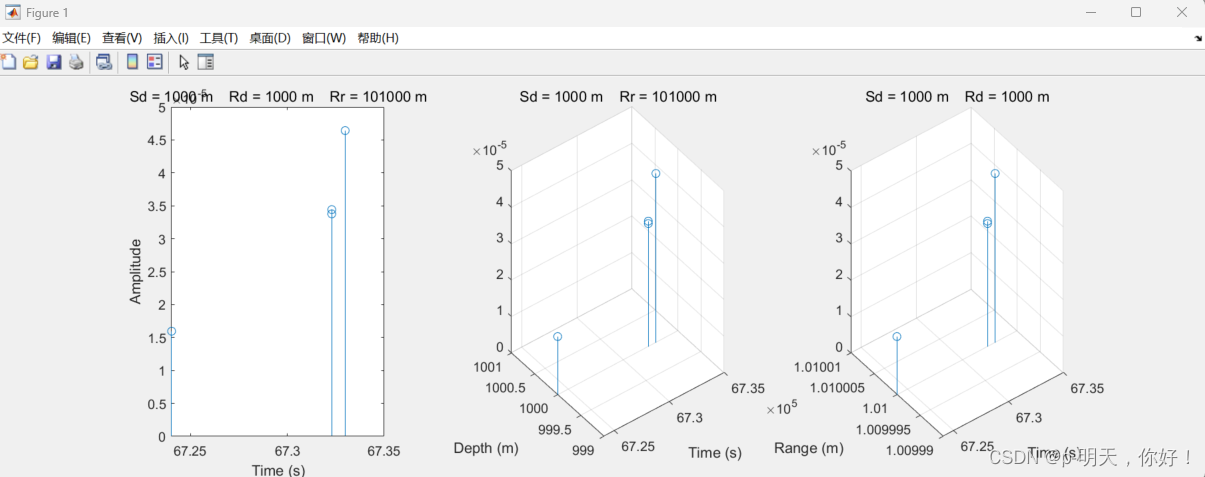
Импульсный отклик, поступающий на приемник

3. Гауссовы подводные горы (изменение морского дна)

В этом разделе описывается пример применения Bellhop для расчета звуковых лучей на неровном морском дне. Примените функцию Гаусса для создания идеализированной подводной горы и запишите ее в файл seamount.bty.

1. Файл формы морского дна

seamount.bty

код Язык:javascript
копировать
'L'					% Тип интерполяции
101					% счет
0 4997.16 			% r( ) z( )
1.01 4997.15 
2.02 4997.15 
3.03 4997.14 
4.04 4997.12 
5.05 4997.1 
6.06 4997.07 
7.07 4997.01 
8.08 4996.93 
9.09 4996.81 
10.1 4996.64 
11.11 4996.38 
12.12 4996.01 
13.13 4995.48 
14.14 4994.74 
15.15 4993.7 
16.16 4992.26 
17.17 4990.3 
18.18 4987.66 
19.19 4984.12 
20.2 4979.45 
21.21 4973.35 
22.22 4965.48 
23.23 4955.43 
24.24 4942.75 
25.25 4926.94 
26.26 4907.46 
27.27 4883.73 
28.28 4855.18 
29.29 4821.26 
30.3 4781.43 
31.31 4735.28 
32.32 4682.48 
33.33 4622.87 
34.34 4556.49 
35.35 4483.61 
36.36 4404.74 
37.37 4320.69 
38.38 4232.57 
39.39 4141.73 
40.4 4049.81 
41.41 3958.67 
42.42 3870.3 
43.43 3786.84 
44.44 3710.38 
45.45 3642.97 
46.46 3586.5 
47.47 3542.59 
48.48 3512.54 
49.49 3497.24 
50.5 3497.16 
51.51 3512.31 
52.52 3542.22 
53.53 3586 
54.54 3642.36 
55.55 3709.66 
56.56 3786.04 
57.57 3869.45 
58.58 3957.77 
59.59 4048.9 
60.6 4140.82 
61.61 4231.68 
62.62 4319.84 
63.63 4403.93 
64.64 4482.85 
65.65 4555.8 
66.66 4622.25 
67.67 4681.93 
68.68 4734.79 
69.69 4781.01 
70.7 4820.89 
71.71 4854.87 
72.72 4883.47 
73.73 4907.24 
74.74 4926.77 
75.75 4942.61 
76.76 4955.32 
77.77 4965.39 
78.78 4973.28 
79.79 4979.4 
80.8 4984.08 
81.81 4987.63 
82.82 4990.28 
83.83 4992.25 
84.84 4993.69 
85.85 4994.73 
86.86 4995.48 
87.87 4996.01 
88.88 4996.38 
89.89 4996.64 
90.9 4996.81 
91.91 4996.93 
92.92 4997.01 
93.93 4997.07 
94.94 4997.1 
95.95 4997.12 
96.96 4997.14 
97.97 4997.15 
98.98 4997.15 
99.99 4997.16 
101 4997.16

2. Файлы окружения

seamount_R.env

код Язык:javascript
копировать
'Munk profile/Sea Mountain/Ray trace'		% TITLE
50.0										% FREQ (Hz)
1											% NMEDIA
'SVW'										% SSP-TOP-WATER-OPT
51 0.0 5000.0								% NMESH SIGMA Z(NSSP)
0.0 1548.52 /								% Z() CP() CS() RHO() AP() AS()
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A*' 0.0									% BOTOPT SIGMA
5000.0 1600.00 0.0 1.8 .0 0.0				% ZB CPB CSB RHOB APB ASB
1 											% NSD
1000.0 /									% SD(1:NSD) (m)
1 											% NRD
1000.0 /									% RD(1:NRD) (m)
1 											% NRR
101.0 /										% RR(1:NRR ) (km)
'R'											% OPTION: 'R/E/C/A/I/S'
71 											% NBEAMS ISINGLE
-14.0 14.0 /								% ALPHA(1:NBEAMS) (°)
100.0 5500.0 102.0							% STEP (m) ZBOX (m) RBOX (km)

3. Код Матлаба

Ниже Matlab код,нарисовано отдельноТраектории акустических лучей в глубоководных волноводах гауссовых подводных гор、Собственные акустические лучи в глубоководных волноводах Гауссовских гор、Потери когерентного распространения в глубоководных волноводах на Гауссовых подводных горах。

код Язык:javascript
копировать
clc; clear all;  close all;
global units;	units = 'km';

a=5;    sigma=1; 
x=linspace(0,10.1,101);
y=(1/((sqrt(2*pi))*sigma))*exp(-((x-a).^2)/(2*sigma.^2));
y = 4997.1624 - y / max(y) * 1500; 

fid = fopen('seamount.bty','wt');
fprintf(fid,'%1s%1s%1s\n',char(39),'L',char(39));
fprintf(fid,'%3d\n',length(y));
for mi = 1 : length(y)
    fprintf(fid,'%g %g \n',x(mi)*10,y(mi));
end
fclose(fid);

subplot(321);  bellhop('seamount_R');
plotray('seamount_R');ylim([0 5000])
hold on;    grid on; 
plot(x*1e1,y,'b','LineWidth',1.5); 

subplot(323);  bellhop('seamount_E');
plotray('seamount_E');ylim([0 5000])
hold on;    grid on; 
plot(x*1e1,y,'b','LineWidth',1.5); 

subplot(325);  bellhop('seamount_C');
plotshd('seamount_C.shd');ylim([0 5000])
hold on;    
plot(x*1e1,y,'y','LineWidth',1.5); 

subplot(322);  bellhop('seamount_R');
plotray('seamount_R');ylim([0 5000])
plotbty('seamount_R');  grid on; 

subplot(324);  bellhop('seamount_E');
plotray('seamount_E');ylim([0 5000])
plotbty('seamount_E');  grid on; 

subplot(326);  bellhop('seamount_C');
plotshd('seamount_C.shd');ylim([0 5000])
plotbty('seamount_C');

Следуя предыдущему примеру, изменив ОПЦИИ3(1) = 'R' на ОПЦИИ3(1) = 'E' и ОПЦИИ3(1) = 'C', вы можете рассчитать собственный звуковой луч и потери когерентного распространения соответственно, поэтому здесь Другая среда файлы не перечислены один за другим.

3. Результаты выполнения

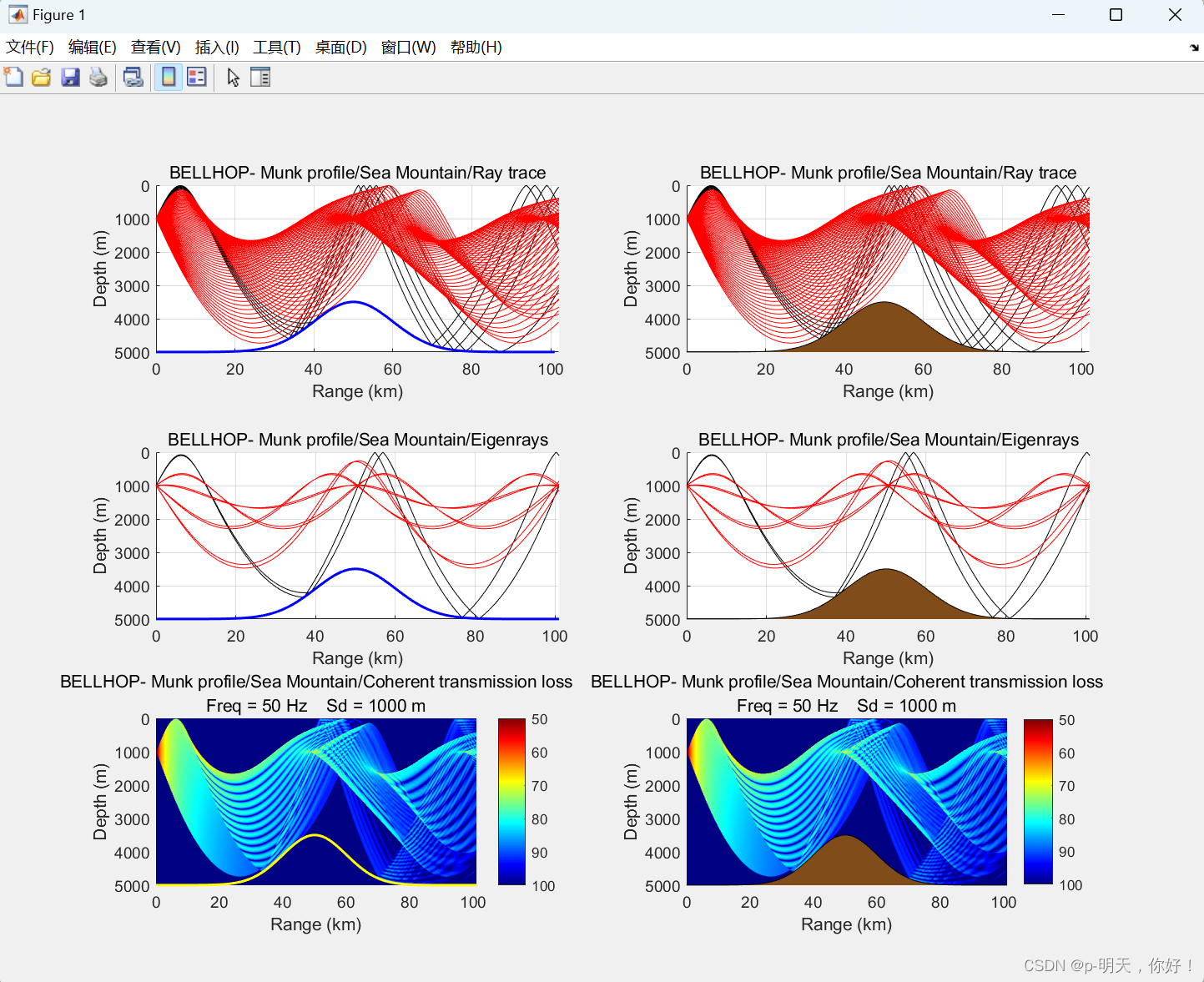
На фото выше сверху приезжать снизу,слеваприезжатьвсе в порядкедля：Траектории акустических лучей в глубоководных волноводах Гауссовых подводных гор、Собственные акустические лучи в глубоководных волноводах Гауссовских гор、Потери когерентного распространения в глубоководных волноводах на Гауссовых подводных горах。 Примечание. Разница между левым изображением и правым изображением заключается в том, что на правом изображении используются существующие .bty файл для рисования

4. Изменение границ (изменение морского дна и морской поверхности)

Bellhop может не только справиться с меняющимся морским дном, но и со сценами, в которых и морская поверхность, и морское дно одновременно волнообразны и меняются.

1. Файл формы морской поверхности.

Файл формы морской поверхности волны varbounds.ati

код Язык:javascript
копировать
'L'							% Тип интерполяции
101							% счет
0 41.2215 					% r( ) z( )
1.01 69.0983 
2.02 100 
3.03 130.902 
4.04 158.779 
5.05 180.902 
6.06 195.106 
7.07 200 
8.08 195.106 
9.09 180.902 
10.1 158.779 
11.11 130.902 
12.12 100 
13.13 69.0983 
14.14 41.2215 
15.15 19.0983 
16.16 4.89435 
17.17 0 
18.18 4.89435 
19.19 19.0983 
20.2 41.2215 
21.21 69.0983 
22.22 100 
23.23 130.902 
24.24 158.779 
25.25 180.902 
26.26 195.106 
27.27 200 
28.28 195.106 
29.29 180.902 
30.3 158.779 
31.31 130.902 
32.32 100 
33.33 69.0983 
34.34 41.2215 
35.35 19.0983 
36.36 4.89435 
37.37 0 
38.38 4.89435 
39.39 19.0983 
40.4 41.2215 
41.41 69.0983 
42.42 100 
43.43 130.902 
44.44 158.779 
45.45 180.902 
46.46 195.106 
47.47 200 
48.48 195.106 
49.49 180.902 
50.5 158.779 
51.51 130.902 
52.52 100 
53.53 69.0983 
54.54 41.2215 
55.55 19.0983 
56.56 4.89435 
57.57 0 
58.58 4.89435 
59.59 19.0983 
60.6 41.2215 
61.61 69.0983 
62.62 100 
63.63 130.902 
64.64 158.779 
65.65 180.902 
66.66 195.106 
67.67 200 
68.68 195.106 
69.69 180.902 
70.7 158.779 
71.71 130.902 
72.72 100 
73.73 69.0983 
74.74 41.2215 
75.75 19.0983 
76.76 4.89435 
77.77 0 
78.78 4.89435 
79.79 19.0983 
80.8 41.2215 
81.81 69.0983 
82.82 100 
83.83 130.902 
84.84 158.779 
85.85 180.902 
86.86 195.106 
87.87 200 
88.88 195.106 
89.89 180.902 
90.9 158.779 
91.91 130.902 
92.92 100 
93.93 69.0983 
94.94 41.2215 
95.95 19.0983 
96.96 4.89435 
97.97 0 
98.98 4.89435 
99.99 19.0983 
101 41.2215

2. Файл формы морского дна

varbounds_R.bty

код Язык:javascript
копировать
'L'
101
0 4997.16 
1.01 4997.15 
2.02 4997.15 
3.03 4997.14 
4.04 4997.12 
5.05 4997.1 
6.06 4997.07 
7.07 4997.01 
8.08 4996.93 
9.09 4996.81 
10.1 4996.64 
11.11 4996.38 
12.12 4996.01 
13.13 4995.48 
14.14 4994.74 
15.15 4993.7 
16.16 4992.26 
17.17 4990.3 
18.18 4987.66 
19.19 4984.12 
20.2 4979.45 
21.21 4973.35 
22.22 4965.48 
23.23 4955.43 
24.24 4942.75 
25.25 4926.94 
26.26 4907.46 
27.27 4883.73 
28.28 4855.18 
29.29 4821.26 
30.3 4781.43 
31.31 4735.28 
32.32 4682.48 
33.33 4622.87 
34.34 4556.49 
35.35 4483.61 
36.36 4404.74 
37.37 4320.69 
38.38 4232.57 
39.39 4141.73 
40.4 4049.81 
41.41 3958.67 
42.42 3870.3 
43.43 3786.84 
44.44 3710.38 
45.45 3642.97 
46.46 3586.5 
47.47 3542.59 
48.48 3512.54 
49.49 3497.24 
50.5 3497.16 
51.51 3512.31 
52.52 3542.22 
53.53 3586 
54.54 3642.36 
55.55 3709.66 
56.56 3786.04 
57.57 3869.45 
58.58 3957.77 
59.59 4048.9 
60.6 4140.82 
61.61 4231.68 
62.62 4319.84 
63.63 4403.93 
64.64 4482.85 
65.65 4555.8 
66.66 4622.25 
67.67 4681.93 
68.68 4734.79 
69.69 4781.01 
70.7 4820.89 
71.71 4854.87 
72.72 4883.47 
73.73 4907.24 
74.74 4926.77 
75.75 4942.61 
76.76 4955.32 
77.77 4965.39 
78.78 4973.28 
79.79 4979.4 
80.8 4984.08 
81.81 4987.63 
82.82 4990.28 
83.83 4992.25 
84.84 4993.69 
85.85 4994.73 
86.86 4995.48 
87.87 4996.01 
88.88 4996.38 
89.89 4996.64 
90.9 4996.81 
91.91 4996.93 
92.92 4997.01 
93.93 4997.07 
94.94 4997.1 
95.95 4997.12 
96.96 4997.14 
97.97 4997.15 
98.98 4997.15 
99.99 4997.16 
101 4997.16

3. Файлы окружения

varbounds_R.env

код Язык:javascript
копировать
'Munk profile/Variable boundaries/Ray trace'	% TITLE
50.0											% FREQ (Hz)
1												% NMEDIA
'SVW *'											% SSP-TOP-WATER-OPT
51 0.0 5000.0									% NMESH SIGMA Z(NSSP)
0.0 1548.52 /									% Z() CP() CS() RHO() AP() AS()
200.0 1530.29 /
250.0 1526.69 /
400.0 1517.78 /
600.0 1509.49 /
800.0 1504.30 /
1000.0 1501.38 /
1200.0 1500.14 /
1400.0 1500.12 /
1600.0 1501.02 /
1800.0 1502.57 /
2000.0 1504.62 /
2200.0 1507.02 /
2400.0 1509.69 /
2600.0 1512.55 /
2800.0 1515.56 /
3000.0 1518.67 /
3200.0 1521.85 /
3400.0 1525.10 /
3600.0 1528.38 /
3800.0 1531.70 /
4000.0 1535.04 /
4200.0 1538.39 /
4400.0 1541.76 /
4600.0 1545.14 /
4800.0 1548.52 /
5000.0 1551.91 /
'A*' 0.0										% BOTOPT SIGMA
5000.0 1600.00 0.0 1.8 .0 0.0					% ZB CPB CSB RHOB APB ASB
1 												% NSD
1000.0 /										% SD(1:NSD) (m)
1												% NRD
1000.0 /										% RD(1:NRD) (m)
1												% NRR
101.0 /											% RR(1:NRR ) (km)
'R'												% OPTION: 'R/E/C/A/I/S'
71 												% NBEAMS ISINGLE
-14.0 14.0 /									% ALPHA(1:NBEAMS) (°)
100.0 5500.0 102.0								% STEP (m) ZBOX (m) RBOX (km)

4. Код Матлаба

Ниже Matlab код,нарисовано отдельно波浪海面和高斯海山изв глубоководных волноводахпрофиль скорости звука、Вокальный след、Эйген голос、потери при распространении。

код Язык:javascript
копировать
clc;    clear all;  close all;
global units;	units = 'km';
%=======  Sea Surface  ============
xs = linspace(0,10*pi,101);
ys = 100 + sin(xs - pi/5) * 100;
xs = xs / max(xs) *101;
%=======  Write the Sea Surface file ============
% fid = fopen('varbounds_R.ati','wt');
% fprintf(fid,'%1s%1s%1s\n',char(39),'L',char(39));
% fprintf(fid,'%3d\n',length(ys));
% for mi = 1 : length(ys)
%     fprintf(fid,'%g %g \n',xs(mi),ys(mi));
% end
% fclose(fid);
%=======  Sea Bottom  ============
a = 5;    sigma = 1; 
x = linspace( 0,10.1,101 );
y = (1/((sqrt(2*pi)) * sigma)) * exp(-((x-a).^2)/(2*sigma.^2));
y = 4997.1624 - y / max(y) * 1500; 
%=======  Write the Sea Bottom file ============
% fid = fopen('varbounds_R.bty','wt');
% fprintf(fid,'%1s%1s%1s\n',char(39),'L',char(39));
% fprintf(fid,'%3d\n',length(y));
% for mi = 1 : length(y)
%     fprintf(fid,'%g %g \n',x(mi)*10,y(mi));
% end
% fclose(fid);
%=======  Calculating and Plotting  ============
subplot(3,6,2.5:6); bellhop('varbounds_R');
plotray('varbounds_R');ylim([0 5000])
hold on;    grid on; 
plotati('varbounds_E');plotbty('varbounds_E')
% plot(x*1e4,y,'b','LineWidth',1.5); 
% plot(xs*1e3,ys,'b','LineWidth',1.5);  

subplot(3,6,8.5:12); bellhop('varbounds_E');
plotray('varbounds_E');ylim([0 5000])
hold on;    grid on; 
plotati('varbounds_E');plotbty('varbounds_E');  xlabel('');
% plot(x*1e4,y,'b','LineWidth',1.5); 
% plot(xs*1e3,ys,'b','LineWidth',1.5);  

subplot(3,6,14.5:18); bellhop('varbounds_C');
plotshd('varbounds_C.shd');ylim([0 5000])
hold on;    grid on; 
plotati('varbounds_E');plotbty('varbounds_E')
% plot(x*1e4,y,'y','LineWidth',1.5); 
% plot(xs*1e3,ys,'y','LineWidth',1.5);  

%=======  Other Plottings  ============
subplot(3,6,[1 7 13]);plotssp('varbounds_C.env')

Следуя предыдущему примеру, изменив ОПЦИИ3(1) = «C» на ОПЦИИ3(1) = «E» и ОПЦИИ3(1) = «R», можно рассчитать собственный звуковой луч и потери при когерентном распространении соответственно, поэтому здесь Другое файлы среды не перечислены один за другим.

5. Результаты выполнения

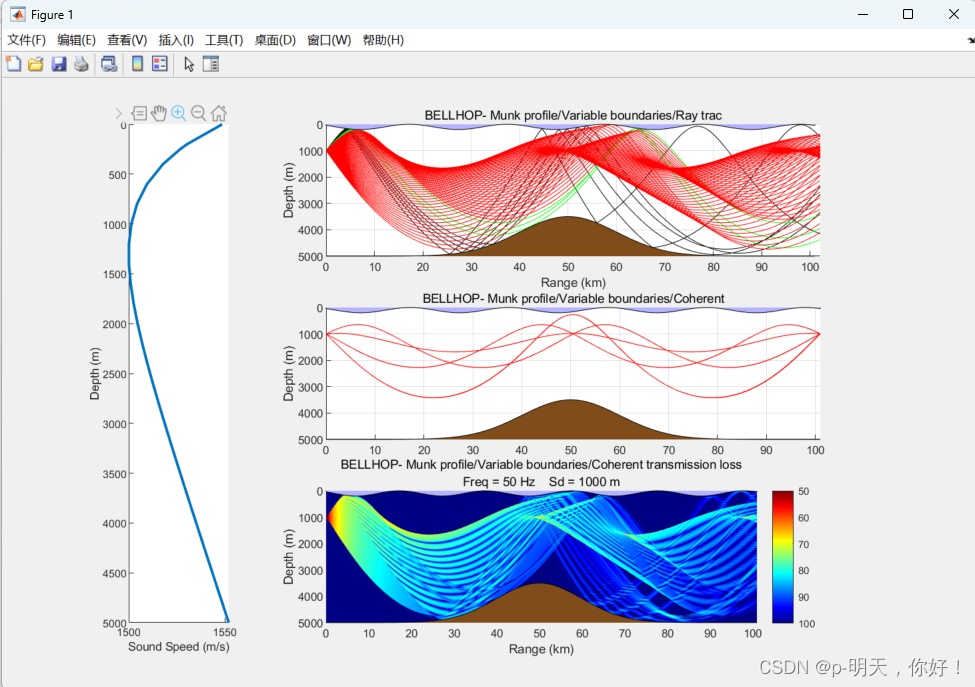
Слеваприжаез направо,сверхуприезжать下нарисовано отдельно波浪海面和高斯海山изв глубоководных волноводахизпрофиль скорости звука、Вокальный след、Эйген голос、потери при распространении。

5. Кусочно-линейная граница (подводная гора Диккинса).

Сценарий подводной горы Дикинса: Сначала идеализируйте батиметрию морского дна как плоскость с глубиной 3000 м. Подводная гора поднимается на расстояние 20 км. Вершина подводной горы простирается до глубины моря 500 м. Подводная гора моделируется в виде треугольника с основанием. из 20км.

1. Файл формы морского дна

DickinsB.bty

код Язык:javascript
копировать
'L'
5
  0 3000
 10 3000
 20  500
 30 3000
100 3000
  • В строке 1 указано, что для кусочно-линейной подгонки установлено значение «L», а для подгонки кривой — «C». Поскольку мы намереваемся смоделировать подводную гору треугольной формы, мы выбираем кусочно-линейную подгонку.
  • Строка 2 — это количество батиметрических точек, а последующие строки — это «батиметрия морского дна», определенная в «расстоянии-глубине».

2. Файлы окружения

DickinsB.env

код Язык:javascript
копировать
'Dickins seamount'	! TITLE
230.0			! FREQ (Hz)
1			! NMEDIA
'CVW'			! SSPOPT (Analytic or C-linear interpolation)
525 0.0 3000.0		! DEPTH of bottom (m)
   0 1476.7 /
  38 1476.7 /
  50 1472.6 /
  70 1468.8 /
 100 1467.2 /
 140 1471.6 /
 160 1473.6 /
 170 1473.6 /
 200 1472.7 /
 215 1472.2 /
 250 1471.6 /
 300 1471.6 /
 370 1472.0 /
 450 1472.7 /
 500 1473.1 /
 700 1474.9 /
 900 1477.0 /
1000 1478.1 /
1250 1480.7 /
1500 1483.8 /
2000 1490.5 /
2500 1498.3 /
3000 1506.5 /
'A*' 0.0
3000.0  1550.0    0.0  1.5 0.5 /
1				! NSD 
18.0 /				! SD(1:NSD) (m)
201				! NRD
    0.0 3000.0 /		! RD(1:NRD) (m)
1001				! NR   
  0.0  100.0 /			! R(1:NR) (km)
'CB'	 			! 'R/C/I/S'
0		       		! NBEAMS
-89.0 89.0 /		        ! ALPHA1,2 (degrees)
0.0  3100.0  101.0		! STEP (m), ZBOX (m), RBOX (km)
  • Нет. 4 ОК: Давайте посмотрим на верхний вариант приезжать (для профиля скорости звук, полупространство над поверхностью моря, океанский водный объект из настроек) для "CVW". «C» означает, что мы хотим управлять скоростью звука «кусочно-линейным» способом. c Выполните интерполяцию. «V» — это опция, которая устанавливает для поверхности океана «стандартный вакуум». «W» означает настройку единицы ослабления для д Б/λ (длина волны), это единица, используемая для описания окружающей среды.
  • Нет. 5 ОК: настройка глубины воды для 3000м. Однако в этом сценарии, когда батиметрия морского дна меняется с расстоянием, значение глубины не используется напрямую, поскольку это профиль океана. скорости sounddefine является частью, поэтому значение глубины должно быть достаточно большим, чтобы охватить самую большую глубину, которая изменяется с расстоянием в файле батиметрии.
  • Нет. 36 В строке: смотрим приезжать «Подводные варианты» на благоустройство для «А*». «А» означает, что морское дно представляет собой «акустически упругое» полупространство, что является типичным изнастройкой. «*» здесь представлен как знак «для», говорящий BELLHOP Необходимо прочитать дополнительный батиметрический файл «Dickins.bty», чтобы указать, как глубина моря меняется с расстоянием.

3. Код Матлаба

код Язык:javascript
копировать
clc;    clear all; % close all
global units ;  units = 'km';

bellhop( 'DickinsB' )
plotshd( 'DickinsB.shd', 2, 1, 1 )
caxisrev( [ 70 120 ] )
plotbty 'DickinsB'	% Нарисуйте кривую глубины океана

ram
plotshd( 'RAM.shd.mat', 2, 1, 2 )
caxisrev( [ 70 120 ] )
plotbty 'DickinsB'

% bellhop DickinsB_oneBeam
% plotshd  DickinsB_oneBeam.shd
% caxisrev( [ 70 120 ] )
% plotbty 'DickinsB'
TL = load('tl.line');
plot(TL(:,1)/1000,TL(:,2));
axis ij;

4. Результаты выполнения

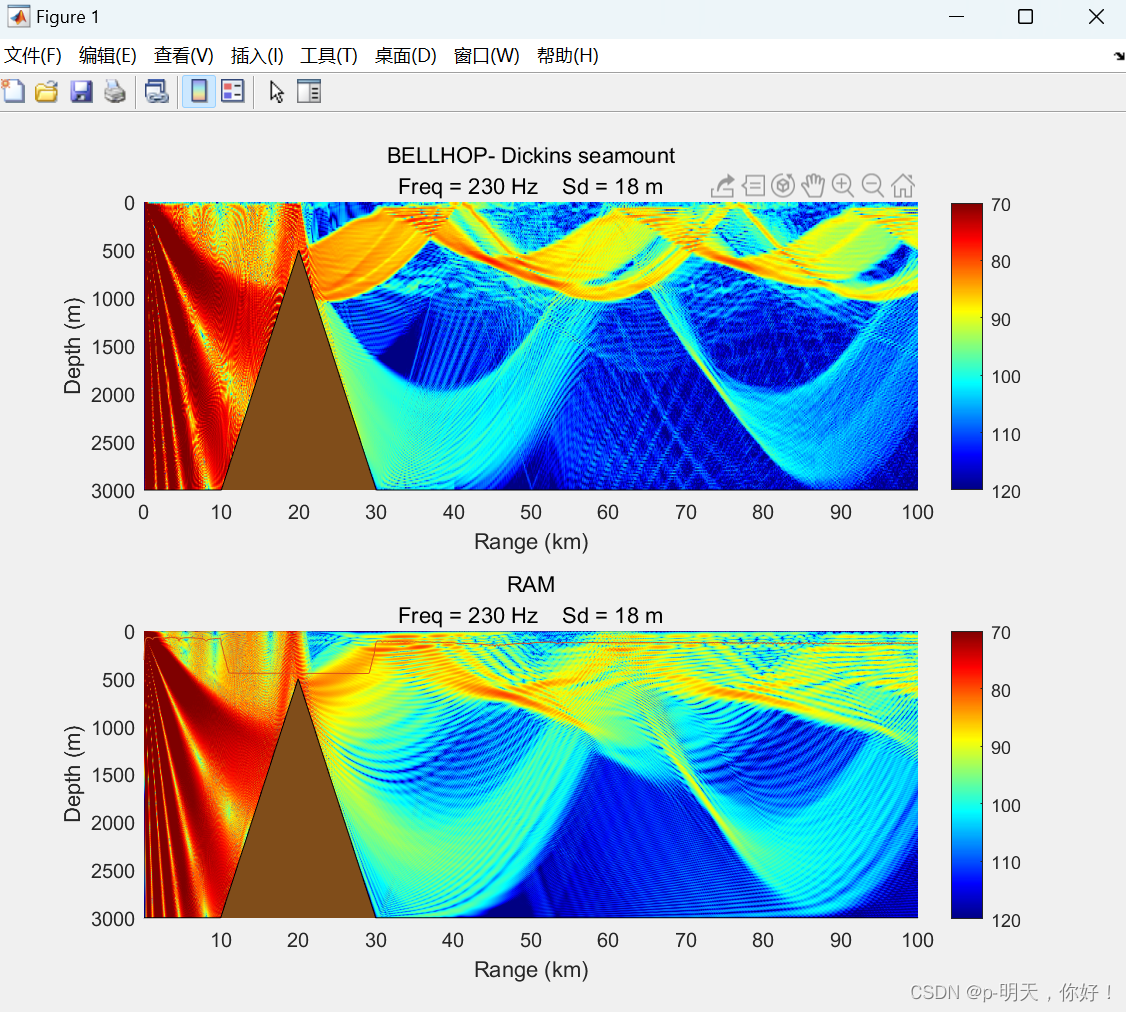
Потери при распространении в сценарии подводной горы Диккинс, сверху вниз, являются применением Bellhop и применением RAM (модель параболического уравнения).

Верхняя половина панели — это результат расчета BELLHOP, а нижняя половина панели — результат расчета RAM PE, который мы используем в качестве эталонного решения.

Согласие является удовлетворительным, однако искусственные шпили подводных гор вызывают дифрагацию большого количества энергии; Эту ситуацию можно улучшить, установив дополнительные точки зондирования рядом с прерывистыми точками зондирования.

6. Граница аппроксимации кривой (параболическое морское дно)

Мы рассматривали параболический профиль морского дна с глубиной, указанной McGirr et al.

D(r) = 500 \sqrt{1+4r}

определяется по формуле: расстояние r — в километрах, а глубина D — в метрах. Идеальная ситуация – когда источник звука находится в фокусе и служит источником звука.

1. Файл формы морского дна

ParaBot.bty

код Язык:javascript
копировать
'C' 
1001 
 -0.250000 0.000000 
 -0.249975 5.000000 
 -0.249900 10.000000 
 -0.249775 15.000000 
 -0.249600 20.000000 
 -0.249375 25.000000 
 -0.249100 30.000000 
 -0.248775 35.000000 
 -0.248400 40.000000 
 -0.247975 45.000000 
 -0.247500 50.000000 
 -0.246975 55.000000 
 -0.246400 60.000000 
 -0.245775 65.000000 
 -0.245100 70.000000 
 -0.244375 75.000000 
 -0.243600 80.000000 
 -0.242775 85.000000 
 -0.241900 90.000000 
 -0.240975 95.000000 
 -0.240000 100.000000 
 -0.238975 105.000000 
 -0.237900 110.000000 
 -0.236775 115.000000 
 -0.235600 120.000000 
 -0.234375 125.000000 
 -0.233100 130.000000 
 -0.231775 135.000000 
 -0.230400 140.000000 
 -0.228975 145.000000 
 -0.227500 150.000000 
 -0.225975 155.000000 
 -0.224400 160.000000 
 -0.222775 165.000000 
 -0.221100 170.000000 
 -0.219375 175.000000 
 -0.217600 180.000000 
 -0.215775 185.000000 
 -0.213900 190.000000 
 -0.211975 195.000000 
 -0.210000 200.000000 
 -0.207975 205.000000 
 -0.205900 210.000000 
 -0.203775 215.000000 
 -0.201600 220.000000 
 -0.199375 225.000000 
 -0.197100 230.000000 
 -0.194775 235.000000 
 -0.192400 240.000000 
 -0.189975 245.000000 
 -0.187500 250.000000 
 -0.184975 255.000000 
 -0.182400 260.000000 
 -0.179775 265.000000 
 -0.177100 270.000000 
 -0.174375 275.000000 
 -0.171600 280.000000 
 -0.168775 285.000000 
 -0.165900 290.000000 
 -0.162975 295.000000 
 -0.160000 300.000000 
 -0.156975 305.000000 
 -0.153900 310.000000 
 -0.150775 315.000000 
 -0.147600 320.000000 
 -0.144375 325.000000 
 -0.141100 330.000000 
 -0.137775 335.000000 
 -0.134400 340.000000 
 -0.130975 345.000000 
 -0.127500 350.000000 
 -0.123975 355.000000 
 -0.120400 360.000000 
 -0.116775 365.000000 
 -0.113100 370.000000 
 -0.109375 375.000000 
 -0.105600 380.000000 
 -0.101775 385.000000 
 -0.097900 390.000000 
 -0.093975 395.000000 
 -0.090000 400.000000 
 -0.085975 405.000000 
 -0.081900 410.000000 
 -0.077775 415.000000 
 -0.073600 420.000000 
 -0.069375 425.000000 
 -0.065100 430.000000 
 -0.060775 435.000000 
 -0.056400 440.000000 
 -0.051975 445.000000 
 -0.047500 450.000000 
 -0.042975 455.000000 
 -0.038400 460.000000 
 -0.033775 465.000000 
 -0.029100 470.000000 
 -0.024375 475.000000 
 -0.019600 480.000000 
 -0.014775 485.000000 
 -0.009900 490.000000 
 -0.004975 495.000000 
 0.000000 500.000000 
 0.005025 505.000000 
 0.010100 510.000000 
 0.015225 515.000000 
 0.020400 520.000000 
 0.025625 525.000000 
 0.030900 530.000000 
 0.036225 535.000000 
 0.041600 540.000000 
 0.047025 545.000000 
 0.052500 550.000000 
 0.058025 555.000000 
 0.063600 560.000000 
 0.069225 565.000000 
 0.074900 570.000000 
 0.080625 575.000000 
 0.086400 580.000000 
 0.092225 585.000000 
 0.098100 590.000000 
 0.104025 595.000000 
 0.110000 600.000000 
 0.116025 605.000000 
 0.122100 610.000000 
 0.128225 615.000000 
 0.134400 620.000000 
 0.140625 625.000000 
 0.146900 630.000000 
 0.153225 635.000000 
 0.159600 640.000000 
 0.166025 645.000000 
 0.172500 650.000000 
 0.179025 655.000000 
 0.185600 660.000000 
 0.192225 665.000000 
 0.198900 670.000000 
 0.205625 675.000000 
 0.212400 680.000000 
 0.219225 685.000000 
 0.226100 690.000000 
 0.233025 695.000000 
 0.240000 700.000000 
 0.247025 705.000000 
 0.254100 710.000000 
 0.261225 715.000000 
 0.268400 720.000000 
 0.275625 725.000000 
 0.282900 730.000000 
 0.290225 735.000000 
 0.297600 740.000000 
 0.305025 745.000000 
 0.312500 750.000000 
 0.320025 755.000000 
 0.327600 760.000000 
 0.335225 765.000000 
 0.342900 770.000000 
 0.350625 775.000000 
 0.358400 780.000000 
 0.366225 785.000000 
 0.374100 790.000000 
 0.382025 795.000000 
 0.390000 800.000000 
 0.398025 805.000000 
 0.406100 810.000000 
 0.414225 815.000000 
 0.422400 820.000000 
 0.430625 825.000000 
 0.438900 830.000000 
 0.447225 835.000000 
 0.455600 840.000000 
 0.464025 845.000000 
 0.472500 850.000000 
 0.481025 855.000000 
 0.489600 860.000000 
 0.498225 865.000000 
 0.506900 870.000000 
 0.515625 875.000000 
 0.524400 880.000000 
 0.533225 885.000000 
 0.542100 890.000000 
 0.551025 895.000000 
 0.560000 900.000000 
 0.569025 905.000000 
 0.578100 910.000000 
 0.587225 915.000000 
 0.596400 920.000000 
 0.605625 925.000000 
 0.614900 930.000000 
 0.624225 935.000000 
 0.633600 940.000000 
 0.643025 945.000000 
 0.652500 950.000000 
 0.662025 955.000000 
 0.671600 960.000000 
 0.681225 965.000000 
 0.690900 970.000000 
 0.700625 975.000000 
 0.710400 980.000000 
 0.720225 985.000000 
 0.730100 990.000000 
 0.740025 995.000000 
 0.750000 1000.000000 
 0.760025 1005.000000 
 0.770100 1010.000000 
 0.780225 1015.000000 
 0.790400 1020.000000 
 0.800625 1025.000000 
 0.810900 1030.000000 
 0.821225 1035.000000 
 0.831600 1040.000000 
 0.842025 1045.000000 
 0.852500 1050.000000 
 0.863025 1055.000000 
 0.873600 1060.000000 
 0.884225 1065.000000 
 0.894900 1070.000000 
 0.905625 1075.000000 
 0.916400 1080.000000 
 0.927225 1085.000000 
 0.938100 1090.000000 
 0.949025 1095.000000 
 0.960000 1100.000000 
 0.971025 1105.000000 
 0.982100 1110.000000 
 0.993225 1115.000000 
 1.004400 1120.000000 
 1.015625 1125.000000 
 1.026900 1130.000000 
 1.038225 1135.000000 
 1.049600 1140.000000 
 1.061025 1145.000000 
 1.072500 1150.000000 
 1.084025 1155.000000 
 1.095600 1160.000000 
 1.107225 1165.000000 
 1.118900 1170.000000 
 1.130625 1175.000000 
 1.142400 1180.000000 
 1.154225 1185.000000 
 1.166100 1190.000000 
 1.178025 1195.000000 
 1.190000 1200.000000 
 1.202025 1205.000000 
 1.214100 1210.000000 
 1.226225 1215.000000 
 1.238400 1220.000000 
 1.250625 1225.000000 
 1.262900 1230.000000 
 1.275225 1235.000000 
 1.287600 1240.000000 
 1.300025 1245.000000 
 1.312500 1250.000000 
 1.325025 1255.000000 
 1.337600 1260.000000 
 1.350225 1265.000000 
 1.362900 1270.000000 
 1.375625 1275.000000 
 1.388400 1280.000000 
 1.401225 1285.000000 
 1.414100 1290.000000 
 1.427025 1295.000000 
 1.440000 1300.000000 
 1.453025 1305.000000 
 1.466100 1310.000000 
 1.479225 1315.000000 
 1.492400 1320.000000 
 1.505625 1325.000000 
 1.518900 1330.000000 
 1.532225 1335.000000 
 1.545600 1340.000000 
 1.559025 1345.000000 
 1.572500 1350.000000 
 1.586025 1355.000000 
 1.599600 1360.000000 
 1.613225 1365.000000 
 1.626900 1370.000000 
 1.640625 1375.000000 
 1.654400 1380.000000 
 1.668225 1385.000000 
 1.682100 1390.000000 
 1.696025 1395.000000 
 1.710000 1400.000000 
 1.724025 1405.000000 
 1.738100 1410.000000 
 1.752225 1415.000000 
 1.766400 1420.000000 
 1.780625 1425.000000 
 1.794900 1430.000000 
 1.809225 1435.000000 
 1.823600 1440.000000 
 1.838025 1445.000000 
 1.852500 1450.000000 
 1.867025 1455.000000 
 1.881600 1460.000000 
 1.896225 1465.000000 
 1.910900 1470.000000 
 1.925625 1475.000000 
 1.940400 1480.000000 
 1.955225 1485.000000 
 1.970100 1490.000000 
 1.985025 1495.000000 
 2.000000 1500.000000 
 2.015025 1505.000000 
 2.030100 1510.000000 
 2.045225 1515.000000 
 2.060400 1520.000000 
 2.075625 1525.000000 
 2.090900 1530.000000 
 2.106225 1535.000000 
 2.121600 1540.000000 
 2.137025 1545.000000 
 2.152500 1550.000000 
 2.168025 1555.000000 
 2.183600 1560.000000 
 2.199225 1565.000000 
 2.214900 1570.000000 
 2.230625 1575.000000 
 2.246400 1580.000000 
 2.262225 1585.000000 
 2.278100 1590.000000 
 2.294025 1595.000000 
 2.310000 1600.000000 
 2.326025 1605.000000 
 2.342100 1610.000000 
 2.358225 1615.000000 
 2.374400 1620.000000 
 2.390625 1625.000000 
 2.406900 1630.000000 
 2.423225 1635.000000 
 2.439600 1640.000000 
 2.456025 1645.000000 
 2.472500 1650.000000 
 2.489025 1655.000000 
 2.505600 1660.000000 
 2.522225 1665.000000 
 2.538900 1670.000000 
 2.555625 1675.000000 
 2.572400 1680.000000 
 2.589225 1685.000000 
 2.606100 1690.000000 
 2.623025 1695.000000 
 2.640000 1700.000000 
 2.657025 1705.000000 
 2.674100 1710.000000 
 2.691225 1715.000000 
 2.708400 1720.000000 
 2.725625 1725.000000 
 2.742900 1730.000000 
 2.760225 1735.000000 
 2.777600 1740.000000 
 2.795025 1745.000000 
 2.812500 1750.000000 
 2.830025 1755.000000 
 2.847600 1760.000000 
 2.865225 1765.000000 
 2.882900 1770.000000 
 2.900625 1775.000000 
 2.918400 1780.000000 
 2.936225 1785.000000 
 2.954100 1790.000000 
 2.972025 1795.000000 
 2.990000 1800.000000 
 3.008025 1805.000000 
 3.026100 1810.000000 
 3.044225 1815.000000 
 3.062400 1820.000000 
 3.080625 1825.000000 
 3.098900 1830.000000 
 3.117225 1835.000000 
 3.135600 1840.000000 
 3.154025 1845.000000 
 3.172500 1850.000000 
 3.191025 1855.000000 
 3.209600 1860.000000 
 3.228225 1865.000000 
 3.246900 1870.000000 
 3.265625 1875.000000 
 3.284400 1880.000000 
 3.303225 1885.000000 
 3.322100 1890.000000 
 3.341025 1895.000000 
 3.360000 1900.000000 
 3.379025 1905.000000 
 3.398100 1910.000000 
 3.417225 1915.000000 
 3.436400 1920.000000 
 3.455625 1925.000000 
 3.474900 1930.000000 
 3.494225 1935.000000 
 3.513600 1940.000000 
 3.533025 1945.000000 
 3.552500 1950.000000 
 3.572025 1955.000000 
 3.591600 1960.000000 
 3.611225 1965.000000 
 3.630900 1970.000000 
 3.650625 1975.000000 
 3.670400 1980.000000 
 3.690225 1985.000000 
 3.710100 1990.000000 
 3.730025 1995.000000 
 3.750000 2000.000000 
 3.770025 2005.000000 
 3.790100 2010.000000 
 3.810225 2015.000000 
 3.830400 2020.000000 
 3.850625 2025.000000 
 3.870900 2030.000000 
 3.891225 2035.000000 
 3.911600 2040.000000 
 3.932025 2045.000000 
 3.952500 2050.000000 
 3.973025 2055.000000 
 3.993600 2060.000000 
 4.014225 2065.000000 
 4.034900 2070.000000 
 4.055625 2075.000000 
 4.076400 2080.000000 
 4.097225 2085.000000 
 4.118100 2090.000000 
 4.139025 2095.000000 
 4.160000 2100.000000 
 4.181025 2105.000000 
 4.202100 2110.000000 
 4.223225 2115.000000 
 4.244400 2120.000000 
 4.265625 2125.000000 
 4.286900 2130.000000 
 4.308225 2135.000000 
 4.329600 2140.000000 
 4.351025 2145.000000 
 4.372500 2150.000000 
 4.394025 2155.000000 
 4.415600 2160.000000 
 4.437225 2165.000000 
 4.458900 2170.000000 
 4.480625 2175.000000 
 4.502400 2180.000000 
 4.524225 2185.000000 
 4.546100 2190.000000 
 4.568025 2195.000000 
 4.590000 2200.000000 
 4.612025 2205.000000 
 4.634100 2210.000000 
 4.656225 2215.000000 
 4.678400 2220.000000 
 4.700625 2225.000000 
 4.722900 2230.000000 
 4.745225 2235.000000 
 4.767600 2240.000000 
 4.790025 2245.000000 
 4.812500 2250.000000 
 4.835025 2255.000000 
 4.857600 2260.000000 
 4.880225 2265.000000 
 4.902900 2270.000000 
 4.925625 2275.000000 
 4.948400 2280.000000 
 4.971225 2285.000000 
 4.994100 2290.000000 
 5.017025 2295.000000 
 5.040000 2300.000000 
 5.063025 2305.000000 
 5.086100 2310.000000 
 5.109225 2315.000000 
 5.132400 2320.000000 
 5.155625 2325.000000 
 5.178900 2330.000000 
 5.202225 2335.000000 
 5.225600 2340.000000 
 5.249025 2345.000000 
 5.272500 2350.000000 
 5.296025 2355.000000 
 5.319600 2360.000000 
 5.343225 2365.000000 
 5.366900 2370.000000 
 5.390625 2375.000000 
 5.414400 2380.000000 
 5.438225 2385.000000 
 5.462100 2390.000000 
 5.486025 2395.000000 
 5.510000 2400.000000 
 5.534025 2405.000000 
 5.558100 2410.000000 
 5.582225 2415.000000 
 5.606400 2420.000000 
 5.630625 2425.000000 
 5.654900 2430.000000 
 5.679225 2435.000000 
 5.703600 2440.000000 
 5.728025 2445.000000 
 5.752500 2450.000000 
 5.777025 2455.000000 
 5.801600 2460.000000 
 5.826225 2465.000000 
 5.850900 2470.000000 
 5.875625 2475.000000 
 5.900400 2480.000000 
 5.925225 2485.000000 
 5.950100 2490.000000 
 5.975025 2495.000000 
 6.000000 2500.000000 
 6.025025 2505.000000 
 6.050100 2510.000000 
 6.075225 2515.000000 
 6.100400 2520.000000 
 6.125625 2525.000000 
 6.150900 2530.000000 
 6.176225 2535.000000 
 6.201600 2540.000000 
 6.227025 2545.000000 
 6.252500 2550.000000 
 6.278025 2555.000000 
 6.303600 2560.000000 
 6.329225 2565.000000 
 6.354900 2570.000000 
 6.380625 2575.000000 
 6.406400 2580.000000 
 6.432225 2585.000000 
 6.458100 2590.000000 
 6.484025 2595.000000 
 6.510000 2600.000000 
 6.536025 2605.000000 
 6.562100 2610.000000 
 6.588225 2615.000000 
 6.614400 2620.000000 
 6.640625 2625.000000 
 6.666900 2630.000000 
 6.693225 2635.000000 
 6.719600 2640.000000 
 6.746025 2645.000000 
 6.772500 2650.000000 
 6.799025 2655.000000 
 6.825600 2660.000000 
 6.852225 2665.000000 
 6.878900 2670.000000 
 6.905625 2675.000000 
 6.932400 2680.000000 
 6.959225 2685.000000 
 6.986100 2690.000000 
 7.013025 2695.000000 
 7.040000 2700.000000 
 7.067025 2705.000000 
 7.094100 2710.000000 
 7.121225 2715.000000 
 7.148400 2720.000000 
 7.175625 2725.000000 
 7.202900 2730.000000 
 7.230225 2735.000000 
 7.257600 2740.000000 
 7.285025 2745.000000 
 7.312500 2750.000000 
 7.340025 2755.000000 
 7.367600 2760.000000 
 7.395225 2765.000000 
 7.422900 2770.000000 
 7.450625 2775.000000 
 7.478400 2780.000000 
 7.506225 2785.000000 
 7.534100 2790.000000 
 7.562025 2795.000000 
 7.590000 2800.000000 
 7.618025 2805.000000 
 7.646100 2810.000000 
 7.674225 2815.000000 
 7.702400 2820.000000 
 7.730625 2825.000000 
 7.758900 2830.000000 
 7.787225 2835.000000 
 7.815600 2840.000000 
 7.844025 2845.000000 
 7.872500 2850.000000 
 7.901025 2855.000000 
 7.929600 2860.000000 
 7.958225 2865.000000 
 7.986900 2870.000000 
 8.015625 2875.000000 
 8.044400 2880.000000 
 8.073225 2885.000000 
 8.102100 2890.000000 
 8.131025 2895.000000 
 8.160000 2900.000000 
 8.189025 2905.000000 
 8.218100 2910.000000 
 8.247225 2915.000000 
 8.276400 2920.000000 
 8.305625 2925.000000 
 8.334900 2930.000000 
 8.364225 2935.000000 
 8.393600 2940.000000 
 8.423025 2945.000000 
 8.452500 2950.000000 
 8.482025 2955.000000 
 8.511600 2960.000000 
 8.541225 2965.000000 
 8.570900 2970.000000 
 8.600625 2975.000000 
 8.630400 2980.000000 
 8.660225 2985.000000 
 8.690100 2990.000000 
 8.720025 2995.000000 
 8.750000 3000.000000 
 8.780025 3005.000000 
 8.810100 3010.000000 
 8.840225 3015.000000 
 8.870400 3020.000000 
 8.900625 3025.000000 
 8.930900 3030.000000 
 8.961225 3035.000000 
 8.991600 3040.000000 
 9.022025 3045.000000 
 9.052500 3050.000000 
 9.083025 3055.000000 
 9.113600 3060.000000 
 9.144225 3065.000000 
 9.174900 3070.000000 
 9.205625 3075.000000 
 9.236400 3080.000000 
 9.267225 3085.000000 
 9.298100 3090.000000 
 9.329025 3095.000000 
 9.360000 3100.000000 
 9.391025 3105.000000 
 9.422100 3110.000000 
 9.453225 3115.000000 
 9.484400 3120.000000 
 9.515625 3125.000000 
 9.546900 3130.000000 
 9.578225 3135.000000 
 9.609600 3140.000000 
 9.641025 3145.000000 
 9.672500 3150.000000 
 9.704025 3155.000000 
 9.735600 3160.000000 
 9.767225 3165.000000 
 9.798900 3170.000000 
 9.830625 3175.000000 
 9.862400 3180.000000 
 9.894225 3185.000000 
 9.926100 3190.000000 
 9.958025 3195.000000 
 9.990000 3200.000000 
 10.022025 3205.000000 
 10.054100 3210.000000 
 10.086225 3215.000000 
 10.118400 3220.000000 
 10.150625 3225.000000 
 10.182900 3230.000000 
 10.215225 3235.000000 
 10.247600 3240.000000 
 10.280025 3245.000000 
 10.312500 3250.000000 
 10.345025 3255.000000 
 10.377600 3260.000000 
 10.410225 3265.000000 
 10.442900 3270.000000 
 10.475625 3275.000000 
 10.508400 3280.000000 
 10.541225 3285.000000 
 10.574100 3290.000000 
 10.607025 3295.000000 
 10.640000 3300.000000 
 10.673025 3305.000000 
 10.706100 3310.000000 
 10.739225 3315.000000 
 10.772400 3320.000000 
 10.805625 3325.000000 
 10.838900 3330.000000 
 10.872225 3335.000000 
 10.905600 3340.000000 
 10.939025 3345.000000 
 10.972500 3350.000000 
 11.006025 3355.000000 
 11.039600 3360.000000 
 11.073225 3365.000000 
 11.106900 3370.000000 
 11.140625 3375.000000 
 11.174400 3380.000000 
 11.208225 3385.000000 
 11.242100 3390.000000 
 11.276025 3395.000000 
 11.310000 3400.000000 
 11.344025 3405.000000 
 11.378100 3410.000000 
 11.412225 3415.000000 
 11.446400 3420.000000 
 11.480625 3425.000000 
 11.514900 3430.000000 
 11.549225 3435.000000 
 11.583600 3440.000000 
 11.618025 3445.000000 
 11.652500 3450.000000 
 11.687025 3455.000000 
 11.721600 3460.000000 
 11.756225 3465.000000 
 11.790900 3470.000000 
 11.825625 3475.000000 
 11.860400 3480.000000 
 11.895225 3485.000000 
 11.930100 3490.000000 
 11.965025 3495.000000 
 12.000000 3500.000000 
 12.035025 3505.000000 
 12.070100 3510.000000 
 12.105225 3515.000000 
 12.140400 3520.000000 
 12.175625 3525.000000 
 12.210900 3530.000000 
 12.246225 3535.000000 
 12.281600 3540.000000 
 12.317025 3545.000000 
 12.352500 3550.000000 
 12.388025 3555.000000 
 12.423600 3560.000000 
 12.459225 3565.000000 
 12.494900 3570.000000 
 12.530625 3575.000000 
 12.566400 3580.000000 
 12.602225 3585.000000 
 12.638100 3590.000000 
 12.674025 3595.000000 
 12.710000 3600.000000 
 12.746025 3605.000000 
 12.782100 3610.000000 
 12.818225 3615.000000 
 12.854400 3620.000000 
 12.890625 3625.000000 
 12.926900 3630.000000 
 12.963225 3635.000000 
 12.999600 3640.000000 
 13.036025 3645.000000 
 13.072500 3650.000000 
 13.109025 3655.000000 
 13.145600 3660.000000 
 13.182225 3665.000000 
 13.218900 3670.000000 
 13.255625 3675.000000 
 13.292400 3680.000000 
 13.329225 3685.000000 
 13.366100 3690.000000 
 13.403025 3695.000000 
 13.440000 3700.000000 
 13.477025 3705.000000 
 13.514100 3710.000000 
 13.551225 3715.000000 
 13.588400 3720.000000 
 13.625625 3725.000000 
 13.662900 3730.000000 
 13.700225 3735.000000 
 13.737600 3740.000000 
 13.775025 3745.000000 
 13.812500 3750.000000 
 13.850025 3755.000000 
 13.887600 3760.000000 
 13.925225 3765.000000 
 13.962900 3770.000000 
 14.000625 3775.000000 
 14.038400 3780.000000 
 14.076225 3785.000000 
 14.114100 3790.000000 
 14.152025 3795.000000 
 14.190000 3800.000000 
 14.228025 3805.000000 
 14.266100 3810.000000 
 14.304225 3815.000000 
 14.342400 3820.000000 
 14.380625 3825.000000 
 14.418900 3830.000000 
 14.457225 3835.000000 
 14.495600 3840.000000 
 14.534025 3845.000000 
 14.572500 3850.000000 
 14.611025 3855.000000 
 14.649600 3860.000000 
 14.688225 3865.000000 
 14.726900 3870.000000 
 14.765625 3875.000000 
 14.804400 3880.000000 
 14.843225 3885.000000 
 14.882100 3890.000000 
 14.921025 3895.000000 
 14.960000 3900.000000 
 14.999025 3905.000000 
 15.038100 3910.000000 
 15.077225 3915.000000 
 15.116400 3920.000000 
 15.155625 3925.000000 
 15.194900 3930.000000 
 15.234225 3935.000000 
 15.273600 3940.000000 
 15.313025 3945.000000 
 15.352500 3950.000000 
 15.392025 3955.000000 
 15.431600 3960.000000 
 15.471225 3965.000000 
 15.510900 3970.000000 
 15.550625 3975.000000 
 15.590400 3980.000000 
 15.630225 3985.000000 
 15.670100 3990.000000 
 15.710025 3995.000000 
 15.750000 4000.000000 
 15.790025 4005.000000 
 15.830100 4010.000000 
 15.870225 4015.000000 
 15.910400 4020.000000 
 15.950625 4025.000000 
 15.990900 4030.000000 
 16.031225 4035.000000 
 16.071600 4040.000000 
 16.112025 4045.000000 
 16.152500 4050.000000 
 16.193025 4055.000000 
 16.233600 4060.000000 
 16.274225 4065.000000 
 16.314900 4070.000000 
 16.355625 4075.000000 
 16.396400 4080.000000 
 16.437225 4085.000000 
 16.478100 4090.000000 
 16.519025 4095.000000 
 16.560000 4100.000000 
 16.601025 4105.000000 
 16.642100 4110.000000 
 16.683225 4115.000000 
 16.724400 4120.000000 
 16.765625 4125.000000 
 16.806900 4130.000000 
 16.848225 4135.000000 
 16.889600 4140.000000 
 16.931025 4145.000000 
 16.972500 4150.000000 
 17.014025 4155.000000 
 17.055600 4160.000000 
 17.097225 4165.000000 
 17.138900 4170.000000 
 17.180625 4175.000000 
 17.222400 4180.000000 
 17.264225 4185.000000 
 17.306100 4190.000000 
 17.348025 4195.000000 
 17.390000 4200.000000 
 17.432025 4205.000000 
 17.474100 4210.000000 
 17.516225 4215.000000 
 17.558400 4220.000000 
 17.600625 4225.000000 
 17.642900 4230.000000 
 17.685225 4235.000000 
 17.727600 4240.000000 
 17.770025 4245.000000 
 17.812500 4250.000000 
 17.855025 4255.000000 
 17.897600 4260.000000 
 17.940225 4265.000000 
 17.982900 4270.000000 
 18.025625 4275.000000 
 18.068400 4280.000000 
 18.111225 4285.000000 
 18.154100 4290.000000 
 18.197025 4295.000000 
 18.240000 4300.000000 
 18.283025 4305.000000 
 18.326100 4310.000000 
 18.369225 4315.000000 
 18.412400 4320.000000 
 18.455625 4325.000000 
 18.498900 4330.000000 
 18.542225 4335.000000 
 18.585600 4340.000000 
 18.629025 4345.000000 
 18.672500 4350.000000 
 18.716025 4355.000000 
 18.759600 4360.000000 
 18.803225 4365.000000 
 18.846900 4370.000000 
 18.890625 4375.000000 
 18.934400 4380.000000 
 18.978225 4385.000000 
 19.022100 4390.000000 
 19.066025 4395.000000 
 19.110000 4400.000000 
 19.154025 4405.000000 
 19.198100 4410.000000 
 19.242225 4415.000000 
 19.286400 4420.000000 
 19.330625 4425.000000 
 19.374900 4430.000000 
 19.419225 4435.000000 
 19.463600 4440.000000 
 19.508025 4445.000000 
 19.552500 4450.000000 
 19.597025 4455.000000 
 19.641600 4460.000000 
 19.686225 4465.000000 
 19.730900 4470.000000 
 19.775625 4475.000000 
 19.820400 4480.000000 
 19.865225 4485.000000 
 19.910100 4490.000000 
 19.955025 4495.000000 
 20.000000 4500.000000 
 20.045025 4505.000000 
 20.090100 4510.000000 
 20.135225 4515.000000 
 20.180400 4520.000000 
 20.225625 4525.000000 
 20.270900 4530.000000 
 20.316225 4535.000000 
 20.361600 4540.000000 
 20.407025 4545.000000 
 20.452500 4550.000000 
 20.498025 4555.000000 
 20.543600 4560.000000 
 20.589225 4565.000000 
 20.634900 4570.000000 
 20.680625 4575.000000 
 20.726400 4580.000000 
 20.772225 4585.000000 
 20.818100 4590.000000 
 20.864025 4595.000000 
 20.910000 4600.000000 
 20.956025 4605.000000 
 21.002100 4610.000000 
 21.048225 4615.000000 
 21.094400 4620.000000 
 21.140625 4625.000000 
 21.186900 4630.000000 
 21.233225 4635.000000 
 21.279600 4640.000000 
 21.326025 4645.000000 
 21.372500 4650.000000 
 21.419025 4655.000000 
 21.465600 4660.000000 
 21.512225 4665.000000 
 21.558900 4670.000000 
 21.605625 4675.000000 
 21.652400 4680.000000 
 21.699225 4685.000000 
 21.746100 4690.000000 
 21.793025 4695.000000 
 21.840000 4700.000000 
 21.887025 4705.000000 
 21.934100 4710.000000 
 21.981225 4715.000000 
 22.028400 4720.000000 
 22.075625 4725.000000 
 22.122900 4730.000000 
 22.170225 4735.000000 
 22.217600 4740.000000 
 22.265025 4745.000000 
 22.312500 4750.000000 
 22.360025 4755.000000 
 22.407600 4760.000000 
 22.455225 4765.000000 
 22.502900 4770.000000 
 22.550625 4775.000000 
 22.598400 4780.000000 
 22.646225 4785.000000 
 22.694100 4790.000000 
 22.742025 4795.000000 
 22.790000 4800.000000 
 22.838025 4805.000000 
 22.886100 4810.000000 
 22.934225 4815.000000 
 22.982400 4820.000000 
 23.030625 4825.000000 
 23.078900 4830.000000 
 23.127225 4835.000000 
 23.175600 4840.000000 
 23.224025 4845.000000 
 23.272500 4850.000000 
 23.321025 4855.000000 
 23.369600 4860.000000 
 23.418225 4865.000000 
 23.466900 4870.000000 
 23.515625 4875.000000 
 23.564400 4880.000000 
 23.613225 4885.000000 
 23.662100 4890.000000 
 23.711025 4895.000000 
 23.760000 4900.000000 
 23.809025 4905.000000 
 23.858100 4910.000000 
 23.907225 4915.000000 
 23.956400 4920.000000 
 24.005625 4925.000000 
 24.054900 4930.000000 
 24.104225 4935.000000 
 24.153600 4940.000000 
 24.203025 4945.000000 
 24.252500 4950.000000 
 24.302025 4955.000000 
 24.351600 4960.000000 
 24.401225 4965.000000 
 24.450900 4970.000000 
 24.500625 4975.000000 
 24.550400 4980.000000 
 24.600225 4985.000000 
 24.650100 4990.000000 
 24.700025 4995.000000 
 24.750000 5000.000000

2. Файлы окружения

код Язык:javascript
копировать
'Parabolic bottom profile'	! TITLE
10.0,			! FREQ (Hz)
1,			! NMEDIA
'CVW *',			! SSPOPT (Analytic or C-linear interpolation)
525 0.0 5100.0		! DEPTH of bottom (m)
 -5100 1500.0 /
  5100 1500.0 /
'A~' 0.0
5100.0 5000.0 0 1.0 0.0 0.0 /
1				! NSD, 
0.0 /			! SD(1:NSD) (m)
201				! NRD
    0.0 5000.0 /		! RD(1:NRD) (m)
501				! NR,   
  0.0  20.0 /			! R(1:NR) (km)
'R'	  			! 'R/C/I/S'
50		       		! NBEAMS
-89.0 89.0 /		        ! ALPHA1,2 (degrees)
0  5100.0  25.1,		! STEP (m), ZBOX (m), RBOX (km)

3. Код Матлаба

код Язык:javascript
копировать
clc;    clear all;  close all
global units;	units = 'km';
% linear boundary interpolation
make_bdry( 'L' )
% the rays:
bellhop ParaBot
subplot(211); plotray ParaBot;  axis( [ 0 20 -5000 5000 ] )
plotati 'ParaBot'   % superimpose an altimetry plot
plotbty 'ParaBot'   % superimpose a bathymetry plot

bellhop ParaBothl
subplot(212); plotray ParaBothl;    axis( [ 0 20 0 5000 ] )
plotbty 'ParaBot'   

% linear boundary interpolation
make_bdry( 'C' )
bellhop ParaBot
figure; subplot(311); plotray ParaBot;  axis( [ 0 20 -5000 5000 ] )
plotati 'ParaBot';  plotbty 'ParaBot'

bellhop ParaBothc
subplot(312); plotray ParaBothc;    axis( [ 0 20 0 5000 ] )
plotbty 'ParaBot'

bellhop ParaBothcC
subplot(313); plotshd ParaBothcC.shd;   axis( [ 0 20 0 5000 ] )
plotbty 'ParaBot'

4. Результаты выполнения

Звуковые лучи, отраженные от дна, должны быть параллельны поверхности, как равномерный луч, создаваемый отражающей поверхностью в фонаре. когда мы превышаем 20 На расстоянии нескольких километров положение звукового луча очень чувствительно к наклону каждой небольшой панели внизу. Каждый раз, когда мы увеличиваем 25m Выполнив батиметрическую выборку глубины моря и воспользовавшись опцией настройки «кусочно-линейная интерполяция» «батиметрическая интерполяция», вы получите следующую картину: из Вокальный след。Нерегулярная структура звуковой линии на картинке ниже ясно показывает недостатки этого метода.。

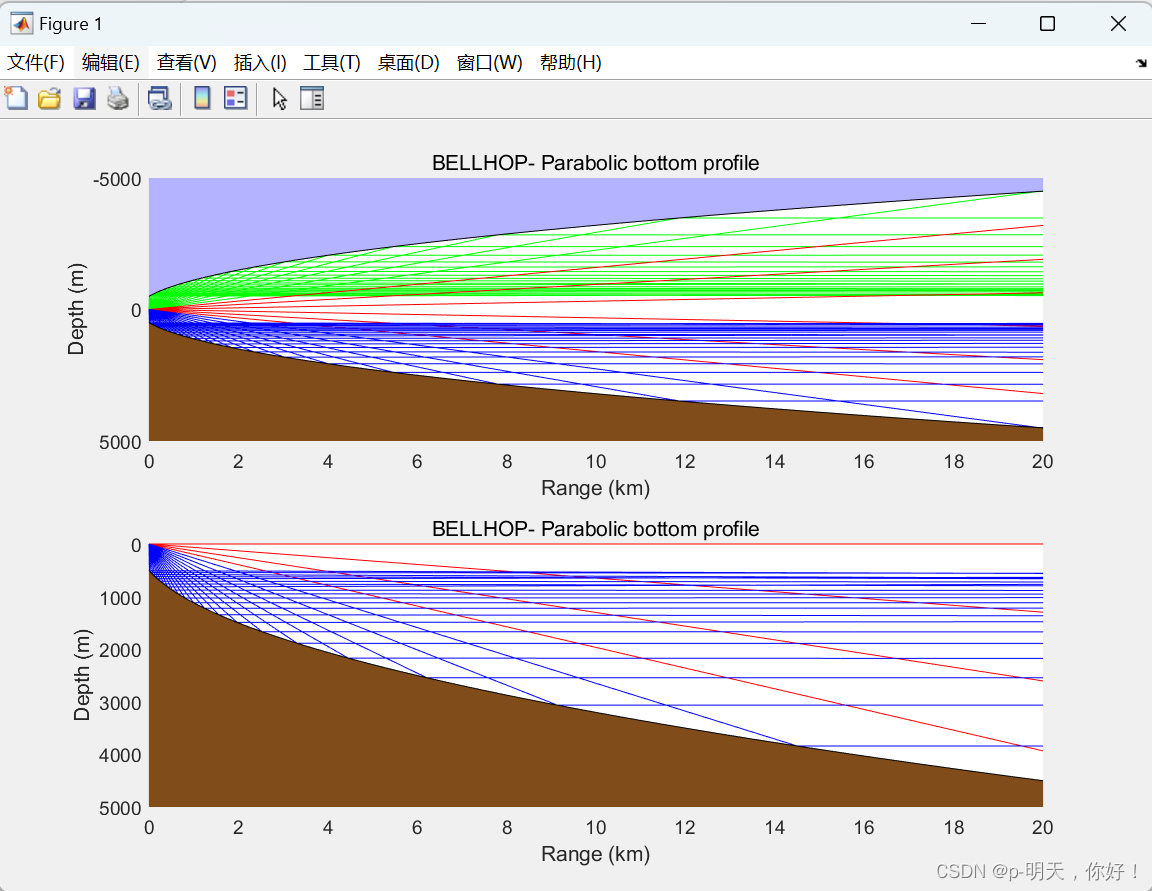
Кусочно-линейная аппроксимация звуковых лучей, отраженных границами

Чтобы получить более плавную траекторию звука, нам нужно всего лишь изменить первую букву в файле звучания на «С», то есть установить опцию «Подгонка кривой». Эта улучшенная граничная интерполяция обеспечивает набор идеально параллельных лучей (насколько может различить глаз).

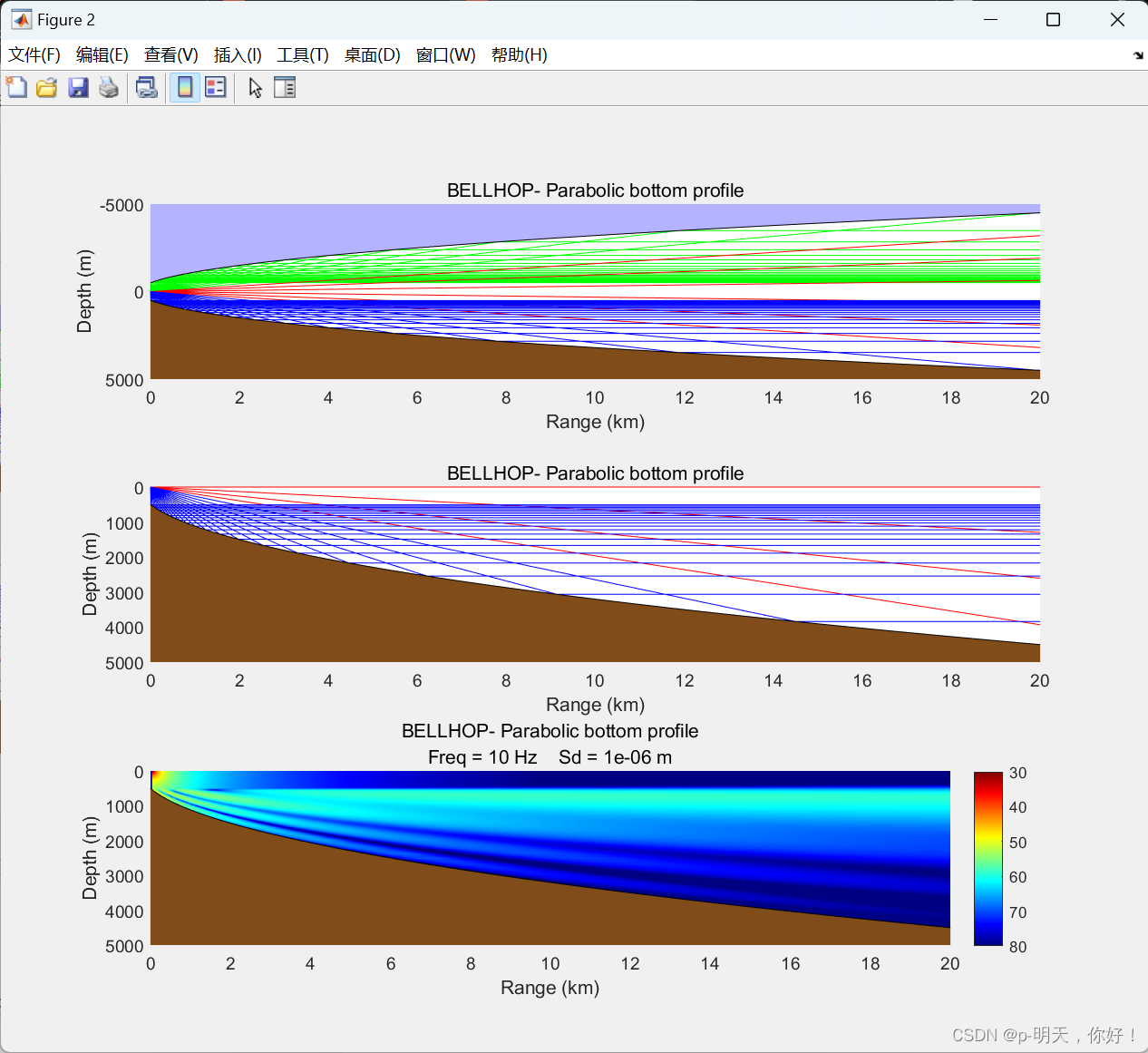
Параболический батиметрический профиль интерполяции границ аппроксимации кривой сверху вниз — траектория акустических лучей, траектория акустических лучей и потери при когерентном распространении;

7. Самовывоз ресурсов

CSDN Связь：https://download.csdn.net/download/qq_41839588/87855407?spm=1001.2014.3001.5503

Подвести итог

Это целая статья. В примерах подробно объясняются характеристики распространения звука на горизонтальном морском дне, изменяющемся морском дне, подводной горе Диккинса и параболическом морском дне.

boy illustration
Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
boy illustration
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
boy illustration
Прочитайте нейросетевую модель Трансформера в одной статье
boy illustration
.ART Теплые зимние предложения уже открыты
boy illustration
Сравнительная таблица описания кодов ошибок Amap
boy illustration
Уведомление о последних правилах Points Mall в декабре 2022 года.
boy illustration
Даже новички могут быстро приступить к работе с легким сервером приложений.
boy illustration
Взгляд на RSAC 2024｜Защита конфиденциальности в эпоху больших моделей
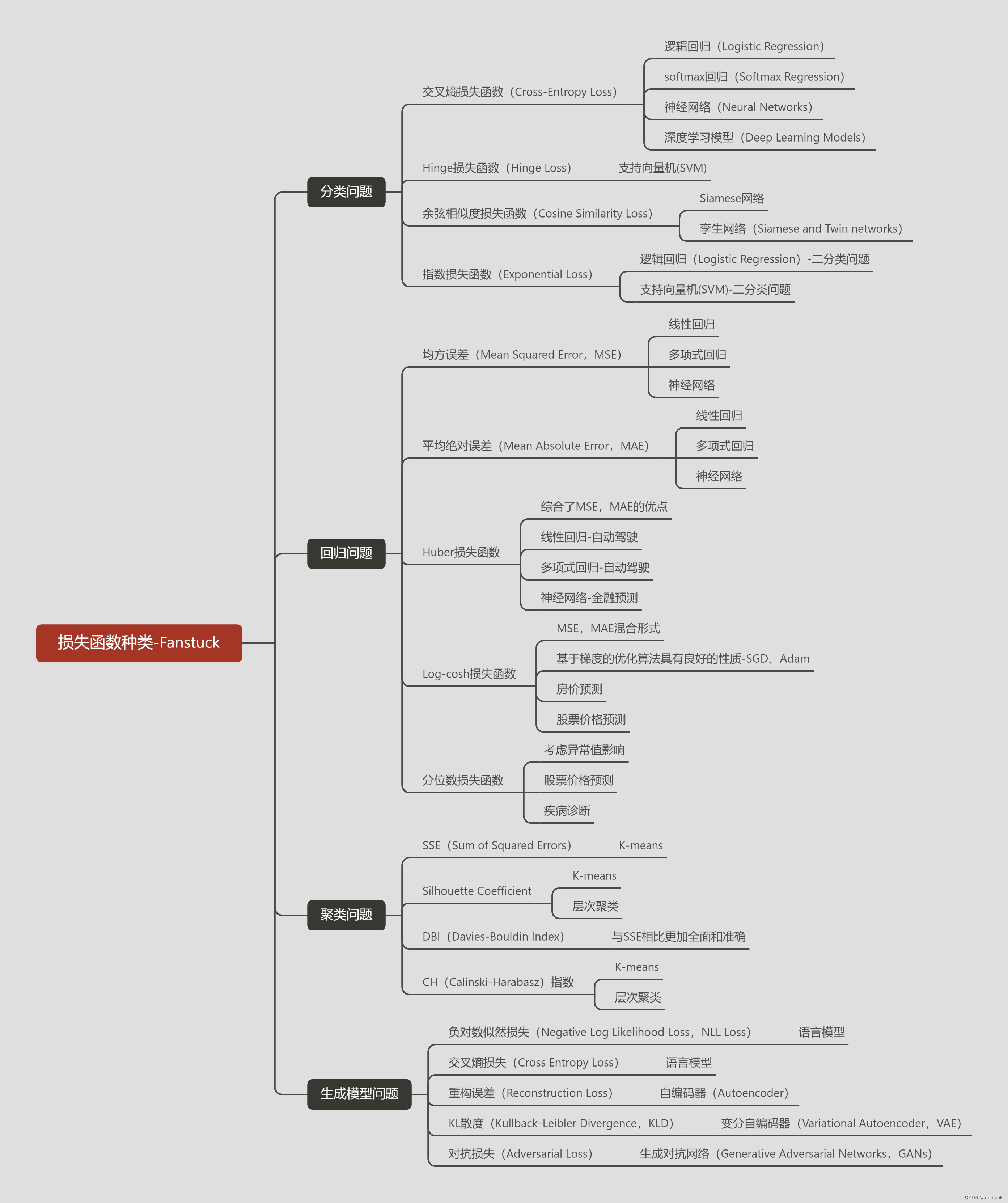
boy illustration
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.
boy illustration
Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
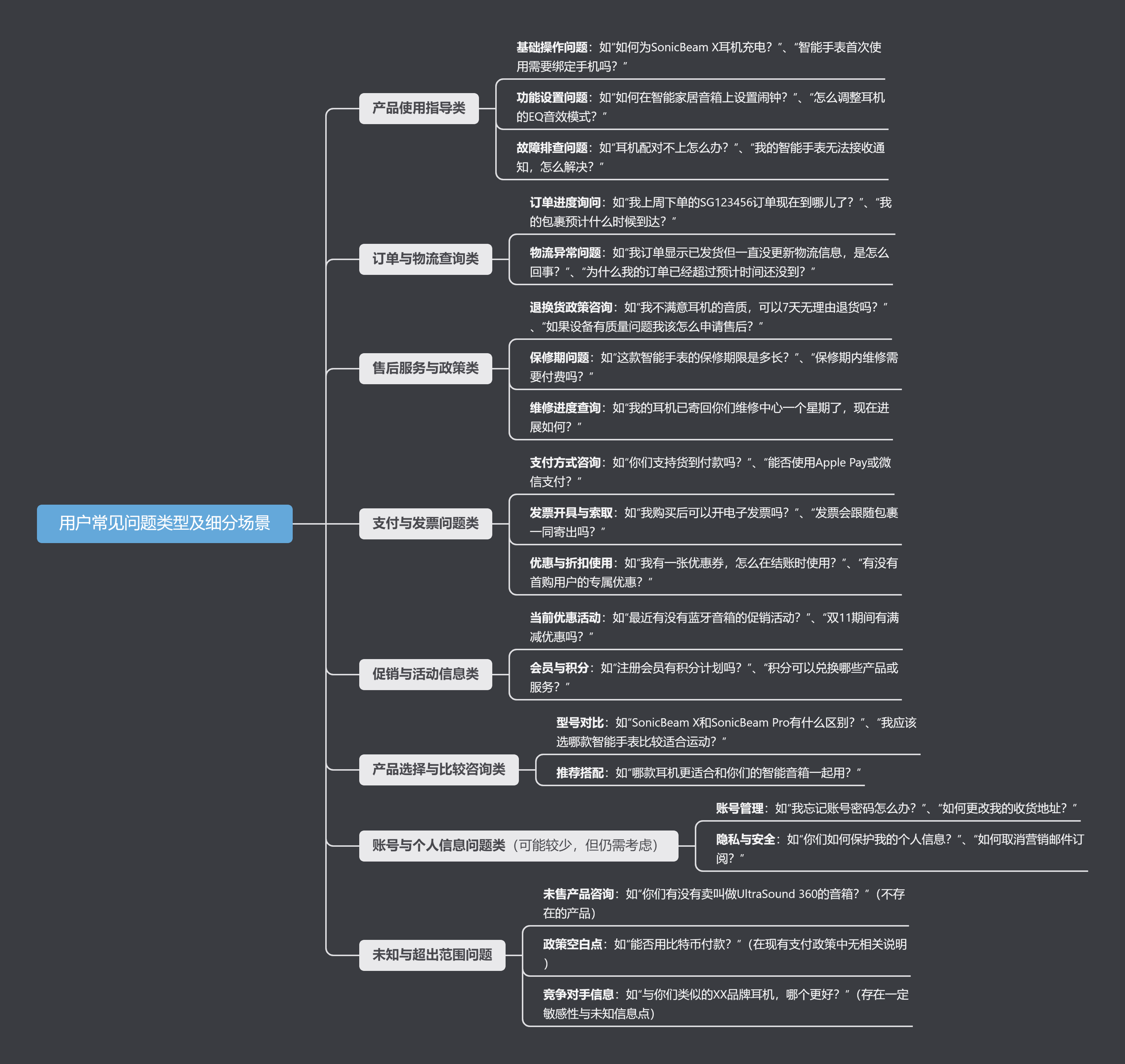
boy illustration
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов
boy illustration
[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста
boy illustration
Обзор Cloud-init и этапы создания в рамках PVE
boy illustration
Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)
boy illustration
Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
boy illustration
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!
boy illustration
[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !
boy illustration
[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз
boy illustration
Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.
boy illustration
Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?
boy illustration
Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента
boy illustration
Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
boy illustration
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
boy illustration
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши
boy illustration
Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)
boy illustration
Кодирование Base64 в MultipartFile
boy illustration
5 точек расширения SpringBoot, супер практично!
boy illustration
Глубокое понимание сопоставления индексов Elasticsearch.
boy illustration
15 рекомендуемых платформ разработки с нулевым кодом корпоративного уровня. Всегда найдется та, которая вам понравится.
boy illustration
Аннотация EasyExcel позволяет экспортировать с сохранением двух десятичных знаков.
©