Диаграмма рассеяния плотности визуализации данных Python Диаграмма рассеяния плотности
График рассеяния плотности(Density Scatter График), также известный как точечный график плотности или оценка. плотности ядра График Рассеяние — это метод предварительного просмотра данных, который в основном используется для отображения распределения большого количества точек данных на двухмерной плоскости. По традиции График рассеянияпо сравнению с,Он использует цвет или затенение для представления плотности точек данных.,Это сделает распределение выставок более интуитивным. График рассеяния плотность может лучше выявить центральную тенденцию и структуру распределения данных, особенно когда объем данных очень велик, что позволяет избежать проблемы графика. рассеяния Проблема путаницы при предварительном просмотре, вызванная перекрытием средних точек.
Основные понятия, используемые в диаграммах рассеяния плотности:
- График рассеяния(Scatter График: базовое двумерное представление данных, используемое для отображения взаимосвязи между двумя переменными. Положение каждой точки данных определяется значениями этих двух переменных. Когда объем данных огромен, многие точки будут перекрываться, что делает невозможным четкое представление о распределении данных.
- Оценка плотности ядра(Kernel Density Оценка (KDE): непараметрический метод оценки функции плотности вероятности случайной величины. Сглаживание используется для заполнения промежутков между отдельными наблюдениями, в результате чего получается непрерывная функция плотности вероятности. КДЕ Обычно это включает в себя выбор функции ядра (например, ядра Гаусса) и полосы пропускания (параметр, который контролирует степень гладкости).
- Цветовое кодирование:существовать График рассеяния плотностисередина,Области различной плотности частоиспользоватьразные цвета или оттенкивыражать,Глубина цвета представляет собой плотность точек данных в области.
Принципы визуализации:
- отображение данных:Сначала положите каждыйданные Точки отображаются на двумерной плоскости.。Это отличается от обычного График Как и рассеяние, этот шаг определяет положение каждой точки на графике.
- оценка плотности:всемданные Отвечатьиспользовать Оценка плотности Алгоритм ядра. Этот шаг выполняется путем размещения «ядра» вокруг каждой точки данных, а затем поиска всех ядер в области, покрытой всем набором данных. В результате получается оценка каждой позиции во всем двумерном пространстве. плотностиценить。
- карта цветов:Согласно полученномуоценка Значения плотности присваивают цвета или оттенки различным областям. Областям с высокой плотностью будет присвоен более темный или более яркий цвет, а областям с низкой плотностью — более светлый или бледный цвет.
- Рендеринг дисплея:в конечном итоге будет Цветовое Раскрывается двухмерная плоскость кодирования, образующая окончательный График. рассеяния плотность. Дополнительно: График на чертеже рассеяния Показывать цветную полосу справа или снизу плотности colorbar。
Зачем использовать диаграмму рассеяния плотности?
- Изучите распределение данных:проходить Цветовое кодирование представляет собой различные уровни плотности, График рассеяния Плотность может выявить различные закономерности, кластеры или тенденции, которые могут быть скрыты в данных. Это особенно полезно для исследовательского анализа, поскольку может помочь исследователям обнаружить непредвиденные связи или модели поведения. Мы можем видеть, в каких областях более плотная концентрация точек данных, а в каких — относительно разреженная. При работе с большими наборами данных, содержащими десятки тысяч точек данных, традиционный График рассеяние может привести к серьезному перенасыщению графика, когда положения различных точек данных на диаграмме перекрываются, что делает невозможным четкое представление о распределении данных. График рассеяния Плотность решает эту проблему, представляя относительную плотность точек данных внутри области, обеспечивая тем самым более четкий и эффективный способ понимания распределения данных.
- Оптимизируйте визуальное представление:График рассеяния Плотность помогает четко отображать данные с помощью таких методов, как градиентные цвета или отображение уровней цвета, по сравнению с традиционным графиком. рассеяния растерянность и размытость. Это облегчает различие между областями с высокой и низкой плотностью, делая общую презентацию более красивой и простой для понимания. Очень гибкий график рассеяния плотность поддерживает различные параметры настройки, такие как настройка карты цветов、прозрачность、отметкаразмерждать,Для соответствия различным типам и размерам наборов данных. также,Его также можно комбинировать с другими методами предварительной визуализации (например, с контурами или сетками) для улучшения выразительности.
- Обнаружение выбросов:График рассеяния плотность может помочь нам выявить выбросы. Если одна область намного плотнее других областей, может быть выброс.
- кластерный анализ:График рассеяния плотность может помочь нам обнаружить области сбора данных. Если определенная область имеет более высокую плотность, то это может быть центр кластера данных.
- Анализ результатов прогнозирования модели:График рассеяния плотностиочень подходитиспользовать ВВизуализациянаблюдениеценитьипримеркаценитьситуация,Можно наблюдать потенциальные отклонения и достоверность прогнозов модели.
- Облегчить принятие решений:существоватьбизнес-аналитика、финансовый анализ、Биометрияждатьполе,Понимание и анализ закономерностей в сложных наборах данных имеет решающее значение для принятия решений. График рассеяния плотности обеспечивает интуитивно понятный способ определения взаимосвязей между ключевыми переменными и динамическими изменениями.,Это помогает лицам, принимающим решения, делать более осознанный выбор на основе глубокой информации.
Таким образом, использование диаграмм рассеяния плотности полезно при работе с крупномасштабными и
или сложные наборы данных. Он не только эффективно решает проблему перерисовки, но также раскрывает структуру и закономерности, скрытые за огромными данными, обеспечивая при этом элегантное и мощное визуальное представление. Будь то научные исследования, промышленность или бизнес, освоение и применение этой технологии значительно повысят способность понимать и использовать данные.
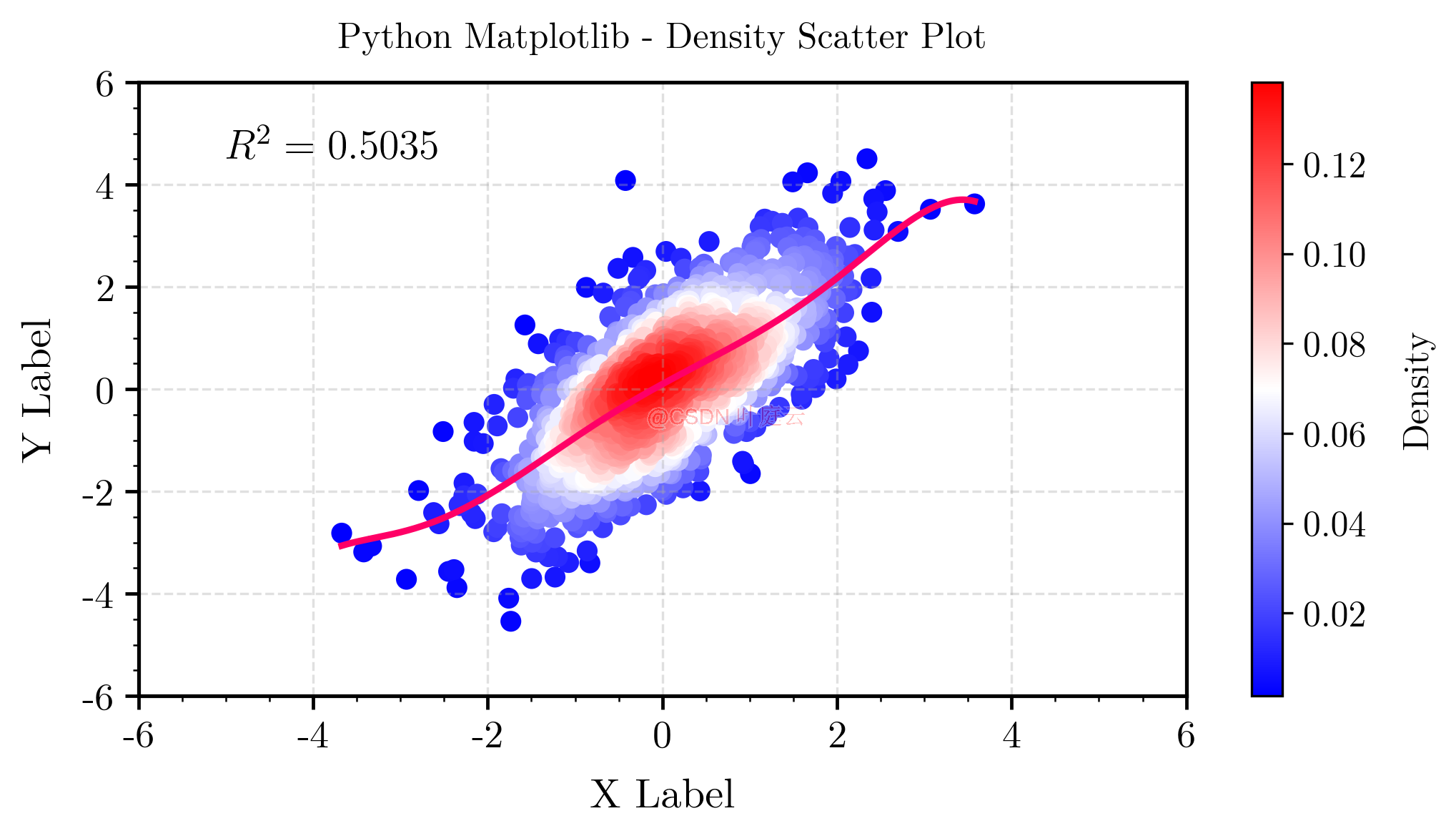
Давайте объясним график с помощью подходящей кривой. рассеяния Пример рисунка плотности。
Импортируйте необходимые зависимые библиотеки:
import numpy as np
from numpy import polyfit, poly1d
import matplotlib as mpl
from matplotlib import cm
from matplotlib import ticker
from matplotlib import colors
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from scipy.stats import gaussian_kdeПостройте диаграмму рассеяния плотности с подобранной кривой Python Код выглядит следующим образом:
# зафиксированный numpy случайное семя
np.random.seed(2024)
# Построение двумерных данных xиy
x = np.random.normal(loc=0.0, scale=1.0, size=1000)
y = x + np.random.normal(loc=0.1, scale=1.0, size=1000)
# Оценка плотности ядра
x_and_y = np.vstack([x, y])
kde = gaussian_kde(x_and_y)
z = kde(x_and_y)
idx = z.argsort()
x, y, z = x[idx], y[idx], z[idx]
is_cbar = True
# Создание графиков и осей
fig, ax = plt.subplots(figsize=(7, 4), dpi=150)
# cmap: bwr、Spectral_r、viridis_r、spring、gist_rainbow_r、RdBu_r
# настраиваемый colormaps - https://matplotlib.org/tutorials/colors/colormaps.html
my_cmap = "bwr"
# График рисования рассеяния плотности
ax.scatter(x, y, c=z, cmap=my_cmap)
# использовать 7 Субполиномиальная аппроксимация,настраиватьиспользовать poly1d Метод получения полиномиальных коэффициентов.
y_fit = polyfit(x, y, 7)
y_fit_1d = np.poly1d(y_fit)
y_hat = np.polyval(y_fit, x)
# Вычислить коэффициент корреляции и R^2
print('Correlation coefficients:')
print(np.corrcoef(y_hat, y))
correlation = np.corrcoef(y_hat, y)[0, 1]
R_square = correlation ** 2
print("R^2:", R_square)
xtick = np.linspace(min(x), max(x), 1000)
# Подобранная полиномиальная кривая
plt.plot(xtick, y_fit_1d(xtick), color="#FF0066", lw=2.2)
# Числовое значение шкалы координатной осииспользовать Latin Modern Math шрифт
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontproperties(font_latex2) for label in labels]
[label.set_color('black') for label in labels]
# Установить масштаб оси
plt.tick_params(axis='x', direction='out', labelsize=13, length=4.6, width=1.15)
plt.tick_params(axis='y', direction='out', labelsize=13, length=4.6, width=1.15)
# выставка XиY субшкала оси
ax.xaxis.set_minor_locator(ticker.AutoMinorLocator())
ax.yaxis.set_minor_locator(ticker.AutoMinorLocator())
# цветная полосанастраивать:шкала、шрифт、Размер шрифтаждать
if is_cbar:
norm = colors.Normalize(vmin=np.min(z), vmax=np.max(z))
cbar = plt.colorbar(cm.ScalarMappable(norm=norm, cmap=my_cmap), ax=ax)
cbar.ax.set_ylabel("Density", fontproperties=font_latex2, labelpad=12)
cbar.ax.tick_params(labelsize=12)
labels = cbar.ax.get_xticklabels() + cbar.ax.get_yticklabels()
[label.set_fontproperties(font_latex2) for label in labels]
[label.set_color('black') for label in labels]
tick_locator = ticker.MaxNLocator(nbins=8)
cbar.locator = tick_locator
cbar.update_ticks()
# настраивать X Ось Y Диапазон значений шкалы оси
ax.set_xlim(left=-6, right=6.0000001)
ax.set_xticks(np.arange(-6, 6.000001, step=2.0))
ax.set_ylim(bottom=-6, top=6.0000001)
ax.set_yticks(np.arange(-6, 6.000001, step=2.0))
# Сделайте рамку вокруг объекта рисования более жирной.
lw = 1.25
ax.spines["right"].set_linewidth(lw)
ax.spines["left"].set_linewidth(lw)
ax.spines["top"].set_linewidth(lw)
ax.spines["bottom"].set_linewidth(lw)
# настраивать X Ось Y метка оси、шрифт、шкалаишкала Этикеткасуществоватьограничивающая рамка оси внутрисерединарасстояние
plt.xlabel("X Label", fontproperties=font_latex1, labelpad=8)
plt.ylabel("Y Label", fontproperties=font_latex1, labelpad=8)
# настраиватьзаголовок шрифт размер и расстояние от объекта рисования
plt.title("Python Matplotlib - Density Scatter Plot",
fontproperties=font_latex2, pad=12
)
# Положение текста определяется на основе координат данных.
ax.text(x=-5, y=4.5, s=r'$\ {R^2} = 0.522$', usetex=True,
fontsize=14, fontweight="bold"
)
# показать сетку Пунктирная линия и прозрачность
plt.grid(alpha=0.360, ls="--", which="major", color="#A9A9A9")
# Компактная планировка
plt.tight_layout()
plt.savefig("./Figures/График рассеяния плотности.png", dpi=300, bbox_inches="tight")
plt.show()Общее объяснение: этот код сначала импортирует необходимые библиотеки, а затем генерирует тестовые данные.
и
(Практическое применение также может быть реальной ценностью.
и прогнозируемая стоимость
). Затем он использует оценку плотности ядра (KDE) для расчета распределения плотности данных. После этого он строит график рассеяния плотности и использует полиномиальную аппроксимацию для создания кривой. Наконец, он вычисляет коэффициент корреляции и
значение и устанавливать различные графические свойства, такие как масштабы осей, цветные полосы, сетки и т. д. Наконец, он сохраняет изображение как .png файл и отображается.
Результаты визуализации следующие::

📚️ Справочные ссылки:
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
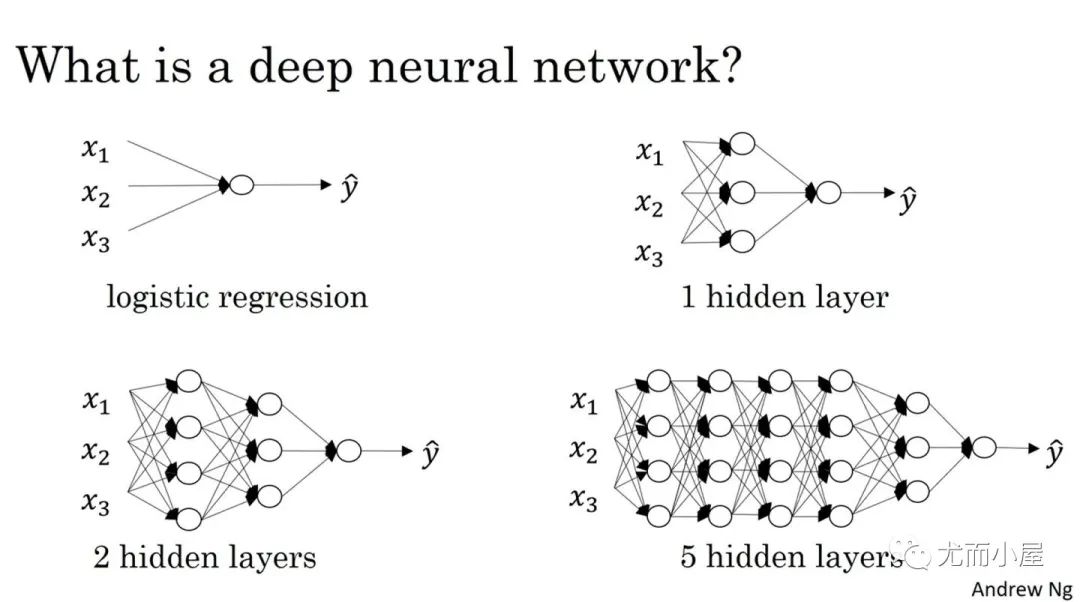
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


