Анализ и оптимизация принципов ПИД-алгоритма
Сегодня я познакомлю вас с классическим управлениемалгоритмодин изПИД-метод регулирования.PIDЭтот метод управления имеет более чем 100-летнюю историю с момента его предложения.,Благодаря простой конструкции, простоте реализации, хорошей прочности и высокой надежности,,В электромеханическом、металлургия、механический、Он широко используется в химической промышленности и других отраслях промышленности.
Когда я учился в колледже, я использовал классический алгоритм ПИД-управления в соревновании по умным автомобилям, в котором я участвовал, что сделало отладку умных автомобилей более удобной.
1. ПИД-принцип
Метод ПИД-управления использует линейную комбинацию пропорционального, интегрального и производного отклонения для формирования управляющей переменной для управления управляемым объектом.
Обычная система ПИД-регулирования показана на рисунке:
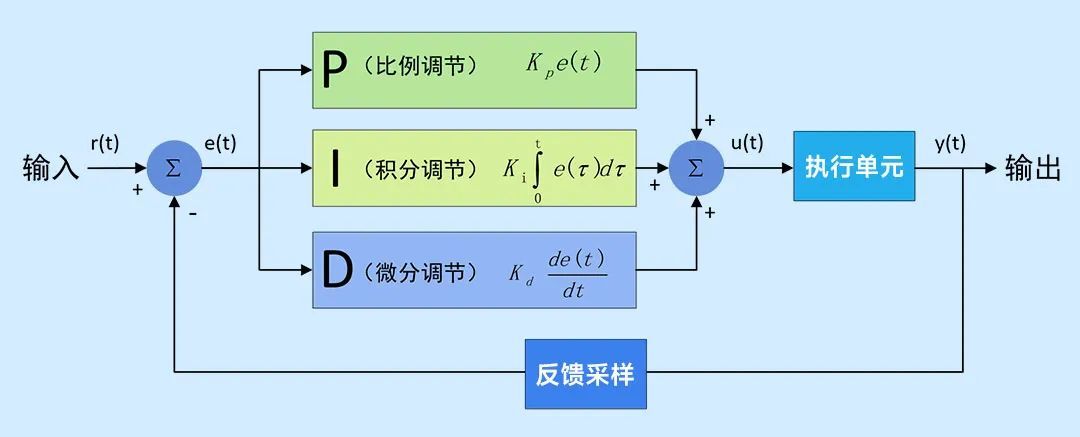
Вход r(t) системы — это целевое выходное значение управляющей величины, выход y(t) — фактическое выходное значение управляющей величины, а e(t) — отклонение между целевым значением и фактическим значением. значение выходной величины. Управление ПИД-алгоритмом осуществляется на основе e(t).
Пропорциональная регулировка – это линейная регулировка, основанная на отклонении между фактическим значением и целевым значением. В системе он выражается как Kpe(t), а Kp — это пропорциональный коэффициент усиления.
Чем больше коэффициент пропорционального усиления Kp, тем более радикальным является эффект регулирования. Небольшие отклонения входных и выходных данных вызывают большие корректировочные действия, и наоборот, чем меньше Kp, тем более консервативен эффект регулирования. эффект корректировки системы не очевиден.
Интегральная корректировка использует накопление исторических отклонений для корректировки выходных данных системы. В системе это выражается как:

Значение интегрального регулирования заключается в устранении установившейся ошибки системы. Чем больше интегральный коэффициент усиления Ki, тем быстрее устраняется установившаяся ошибка системы. Чем меньше Ki, тем сложнее устранить установившуюся ошибку системы и тем хуже точность настройки системы. Однако если Ki слишком велико, это приведет к значительному выбросу в процессе отклика, что приведет к насыщению интеграла.
Дифференциальная регулировка заключается в корректировке выходного сигнала системы на основе скорости изменения отклонения (деривации отклонения), которая выражается в системе как:
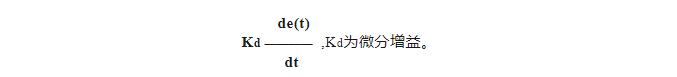
Дифференциальная регулировка в основном играет роль демпфирования и подавления перерегулирования. Чем больше дифференциальный коэффициент усиления Kd, тем лучше стабильность системы и тем меньше колебания кривой в процессе регулировки. Однако, если Kd установлен слишком высоко, время настройки системы будет увеличено, а способность защиты от помех будет ослаблена.
Значение отклонения будет генерировать управляющую величину u(t) после трех типов регулировки, а u(t) будет контролироваться и выводиться через исполнительный блок. Система будет использовать блок выборки для передачи выходных данных на входной терминал для расчета отклонения.
Функциональная связь между u(t) и e(t) в традиционной системе ПИД-регулирования следующая:
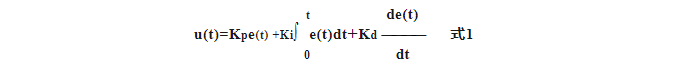
Влияние регулировки параметров Kp, Ki и Kd соответственно на производительность системы ПИД-регулирования показано в следующей таблице:
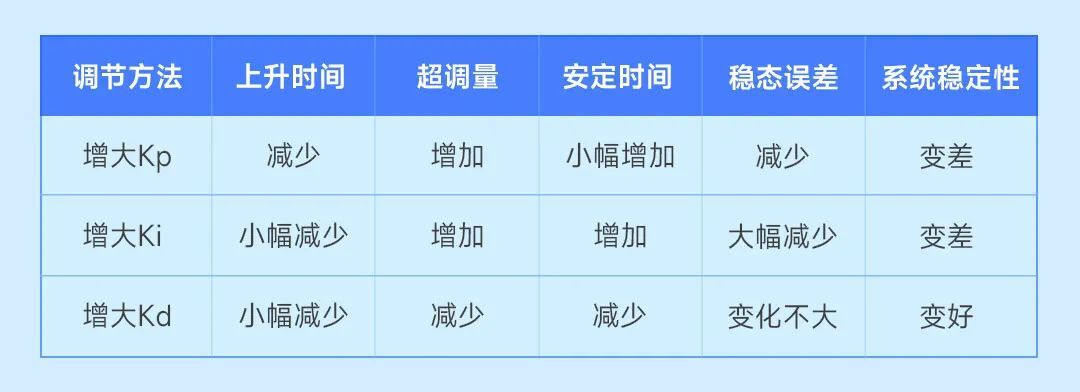
2. Цифровое ПИД-регулирование.
С развитием компьютерных технологий в настоящее время в качестве вычислительного ядра используются микроконтроллеры или компьютеры, а для реализации ПИД-управления и коррекции, то есть цифрового ПИД-управления, используются программы программного обеспечения. Обычно используемые методы цифрового ПИД-регулирования включают в себя: позиционный ПИД, инкрементный ПИД и ступенчатый ПИД.
01
Позиционный ПИД
Поскольку компьютерные операции дискретны, для реализации цифрового ПИД-регулирования сначала необходимо дискретизировать непрерывную функцию.
Используя накопление ошибок для замены интегральной операции, а разность ошибок для замены дифференциальной операции, мы можем получить:
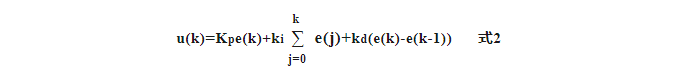
где k — порядковый номер выборки (k=0,1,2,3......),e(k) — значение ошибки при k-й выборке.,e(k-1) — значение ошибки в k-1-й момент выборки. u(k) — выходное значение управляющей величины в k-й момент выборки. В Позиционном ПИД выведите u(k) для непосредственного управления объектом, которым нужно управлять.,Между значением u(k) и объектом управления существует взаимно однозначное соответствие.
Это видно из уравнения 2,Позиционному ПИД необходимо рассчитать погрешность k-го и k-1 раз.,Контроллер накапливает отклонения,Это увеличит вычислительную сложность системы.,Занимает слишком много памяти,Положите нагрузку на компьютер.
В то же время каждый выход u(k) контроллера связан с прошлым состоянием. Большое изменение u(k) приведет к значительному изменению состояния исполнительного механизма, а способность системы к помехам будет плохой. .
Чтобы решить эти проблемы, некоторые ученые предложили другой метод реализации цифрового ПИД-инкрементального ПИД.
02
Инкрементальный ПИД
Выходным сигналом Инкрементального ПИД является приращение Δu(k) к управляемому объекту, а не фактическая величина управления.
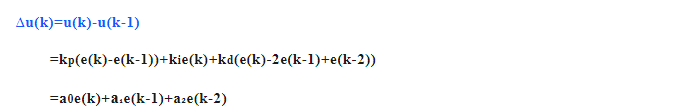
Среди них a0=kp+ki+kd, a₁=-Kp-2kd, a₂=kd.
Из приведенной выше формулы видно, что Инкрементальный ПИД связан с отклонениями в момент времени k, времени k-1 и времени k-2, но отклонения не накапливаются, поэтому по сравнению с Позиционным ПИДСумма расчета меньше,Это не будет связано с прошлыми отклонениями.,Таким образом, стабильность системы управления хорошая.
03
Пошаговый ПИД-регулятор
Когда значение настройки ПИД-системы претерпевает значительные изменения.,система склонна к перерегулированию,повлиять на его стабильность。Чтобы избежать негативного воздействия шаговых сигналов, некоторые учёные предложили Пошаговый ПИД-регулятор.
Пошаговый ПИД-регулятор не реагирует напрямую на сигналы шага.,Вместо этого заданное значение постепенно увеличивается в соответствии с установленными правилами шага.,Заставьте сигнал постепенно приближаться к целевому значению,Таким образом, управляемый объект движется плавно.,Избегается перерегулирование, вызванное мутациями.
Этот метод не меняет саму структуру алгоритма PID, а изменяет заданное значение так, чтобы оно не вызывало мутаций. Существует множество методов пошаговой обработки. Наиболее распространенным из них является установка функции линейного изменения и определение шага изменения. При обнаружении изменения целевого значения заданное значение постепенно корректируется в соответствии с размером шага.
Ys=Yn+kT
Среди них Ys — установленное целевое значение, Yn — текущее целевое значение, T — размер шага и k — коэффициент вариации. Когда обнаруживается, что целевое значение увеличивается, k=1, когда целевое значение не изменяется, k=0, и когда целевое значение уменьшается, k=-1.
Хотя это может уменьшить помехи, вызванные шаговыми сигналами.,Но это также замедлит скорость реакции системы.,Размер шага можно регулировать, чтобы сбалансировать соотношение между двумя。Чем меньше размер шага, тем стабильнее работа и тем медленнее скорость отклика системы, и наоборот.
3. Оптимизация ПИД-алгоритма
01
Интегральная обработка оптимизации насыщения
Если система продолжает иметь отклонение в одном направлении, выходной сигнал ПИД-регулятора увеличивается из-за непрерывного накопления интегральных эффектов, что приводит к выходу контроллера за пределы диапазона и входу в зону насыщения.
Когда в системе возникает обратное отклонение, она не может быстро отреагировать на обратное отклонение из-за выходного насыщения. Это явление называется интегральным насыщением.

Обычно используемые методы подавления насыщения интеграла ПИД включают: Метод интегрального разделения, метод интеграла ограниченного ослабления, метод интеграла переменной скорости и т. д.
//метод интегрального разделения
Когда система обнаруживает, что отклонение e(k) велико, интегральное звено аннулируется. Когда управляемая переменная приближается к заданному значению, ошибка уменьшается, и в это время интегральное звено восстанавливается. Это не повлияет на динамические характеристики контроллера, но также позволит избежать серьезных перерегулирований или непрерывных колебаний.
//метод интегрирования переменной скорости
Скорость интегрирования регулируется в соответствии с отклонением e(k) системы. Когда абсолютное значение e(k) велико, скорость интегрирования замедляется. Когда абсолютное значение e(k) мало, интегрирование. скорость увеличивается. Уменьшение времени интегрирования при насыщении интеграла позволяет добиться эффекта подавления насыщения интеграла и повысить адаптивность системы.
//Метод баллов, который ослабевает при столкновении с ограничениями:
При обнаружении попадания управляющей переменной u(k) в зону насыщения накопление интегрального члена больше не производится, а выполняется операция, ослабляющая интеграл. Это не приведет к слишком сильному перерегулированию и может быстрее реагировать, когда требуется обратная регулировка, не позволяя выходному сигналу оставаться в зоне насыщения в течение длительного времени.
02
Обработка дифференциальной оптимизации терминов
Дифференциальный член в алгоритме ПИД связан со скоростью изменения отклонения. Если в системе есть высокочастотные помехи или мутации, значение дифференциального члена будет продолжать прыгать, вызывая колебания системы в процессе управления и влияя на стабильность системы управления.

Обычно используемые методы оптимизации дифференциальных каналов следующие:
//дифференциальное опережение :
Производная часть действует на отклонение, вызванное измеренным значением, а не на заданное значение. Это позволяет избежать больших колебаний регулировки, вызванных изменениями заданного значения, и подавить колебания системы, вызванные высокочастотными помехами.
//неполный дифференциал :
Неполное дифференцирование вводит инерционное звено первого порядка после дифференциального воздействия, так что величина дифференциальной регулировки, генерируемая при ступенчатом изменении отклонения, выводится относительно плавно. Таким образом, колебания, вызванные мутацией отклонений, могут быть уменьшены без уменьшения эффекта дифференциальной регулировки.
//метод контролируемого дифференцирования :
Дифференциальный ПИД-алгоритм с регулируемой переменной дифференцирует выходное значение контроллера вместо фактического выходного значения реакции системы, что позволяет избежать чрезмерного отклонения реакции системы из-за частых изменений заданного значения системы или больших колебаний привода.
03
Каскадный ПИД-регулятор
так называемый Каскадный ПИД-регулятор,Он использует несколько ПИД-регуляторов для последовательной работы.,Выход контроллера внешнего контура используется в качестве заданного значения контроллера внутреннего контура.,Выход контроллера внутреннего контура управляет контроллером внешнего контура.,Для достижения эффекта управления контролируемой величиной внешнего контура。Каскадный ПИД-регулятор позволяет эффективно повысить качество управления и широко используется при управлении технологическими процессами.
В системе управления доминирует контроллер внешнего контура, с целью обеспечения стабильности основных переменных внешнего контура. Два контроллера координируются и взаимодействуют друг с другом. Контроллер внешнего контура постоянно корректирует заданное значение контроллера внутреннего контура в соответствии с изменениями нагрузки и условий эксплуатации, так что заданное значение контроллера внутреннего контура адаптируется к изменениям нагрузки и условий эксплуатации.
В управлении двигателем очень распространен Каскадный ПИД-регулятор. Обычно используемая структура управления контуром положения + контуром скорости + токовым контуром показана на рисунке.
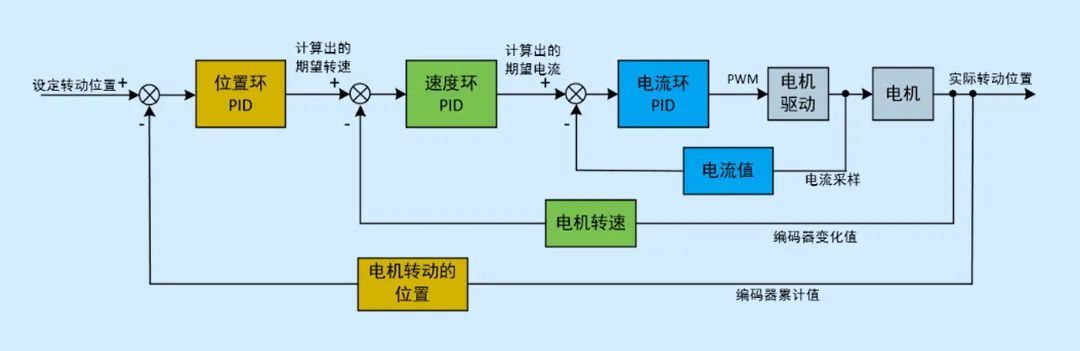
существоватьPIDв методе управленияP、I、Dтри различных регуляторных эффекта,В практических целях три функции регулировки можно гибко комбинировать в соответствии с потребностями.,В этом и прелесть метода ПИД-регулирования.,Его структура определяет его разнообразие и гибкость в практическом применении.
В этой статье в основном дается краткое введение в аспекты принципа ПИД, метода реализации цифрового ПИД и оптимизации алгоритма. Я надеюсь, что она будет полезна всем при изучении алгоритма ПИД.
Учебное пособие по Jetpack Compose для начинающих, базовые элементы управления и макет

Код js веб-страницы, фон частицы, код спецэффектов

【новый! Суперподробное】Полное руководство по свойствам компонентов Figma.
🎉Обязательно к прочтению новичкам: полное руководство по написанию мини-программ WeChat с использованием программного обеспечения Cursor.
[Забавный проект Docker] VoceChat — еще одно приложение для мгновенного чата (IM)! Может быть встроен в любую веб-страницу!

Как реализовать переход по странице в HTML (html переходит на указанную страницу)

Как решить проблему зависания и низкой скорости при установке зависимостей с помощью npm. Существуют ли доступные источники npm, которые могут решить эту проблему?

Серия From Zero to Fun: Uni-App WeChat Payment Practice WeChat авторизует вход в систему и украшает страницу заказа, создает интерфейс заказа и инициирует запрос заказа

Серия uni-app: uni.navigateЧтобы передать скачок значения

Апплет WeChat настраивает верхнюю панель навигации и адаптируется к различным моделям.

JS-время конвертации

Обеспечьте бесперебойную работу ChromeDriver 125: советы по решению проблемы chromedriver.exe не найдены

Поле комментария, щелчок мышью, специальные эффекты, js-код
Объект массива перемещения объекта JS

Как открыть разрешение на позиционирование апплета WeChat_Как использовать WeChat для определения местонахождения друзей
Я даю вам два набора из 18 простых в использовании фонов холста Power BI, так что вам больше не придется возиться с цветами!

Получить текущее время в js_Как динамически отображать дату и время в js

Вам необходимо изучить сочетания клавиш vsCode для форматирования и организации кода, чтобы вам больше не приходилось настраивать формат вручную.

У ChatGPT большое обновление. Всего за 45 минут пресс-конференция показывает, что OpenAI сделал еще один шаг вперед.
Copilot облачной разработки — упрощение разработки

Микросборка xChatGPT с низким кодом, создание апплета чат-бота с искусственным интеллектом за пять шагов

CUDA Out of Memory: идеальное решение проблемы нехватки памяти CUDA
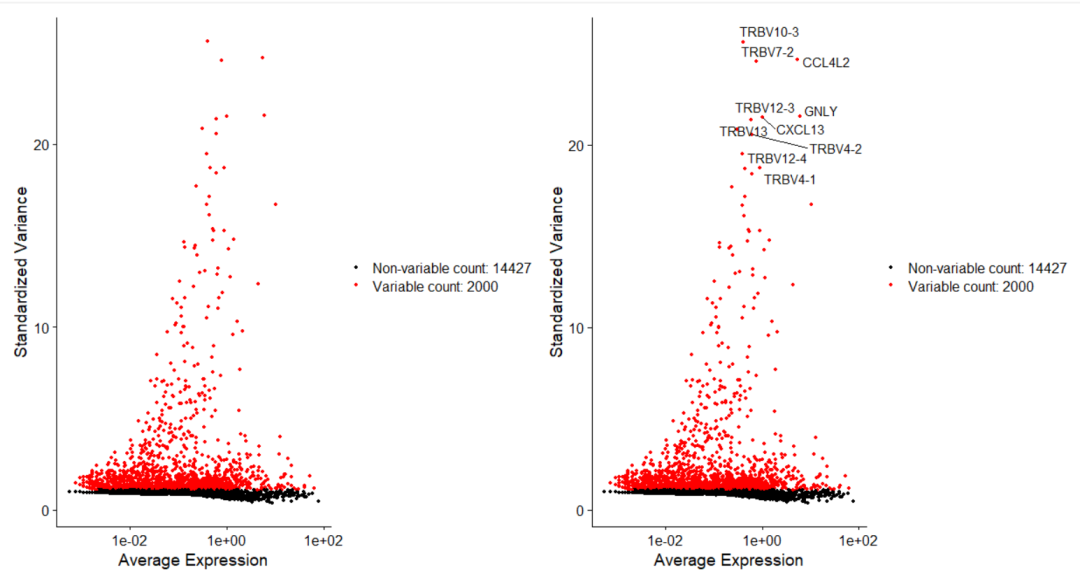
Анализ кластеризации отдельных ячеек, который должен освоить каждый&MarkerгенетическийВизуализация

vLLM: мощный инструмент для ускорения вывода ИИ

CodeGeeX: мощный инструмент генерации кода искусственного интеллекта, который можно использовать бесплатно в дополнение к второму пилоту.

Машинное обучение Реальный бой LightGBM + настройка параметров случайного поиска: точность 96,67%
Бесшовная интеграция, мгновенный интеллект [1]: платформа больших моделей Dify-LLM, интеграция без кодирования и встраивание в сторонние системы, более 42 тысяч звезд, чтобы стать свидетелями эксклюзивных интеллектуальных решений.
LM Studio для создания локальных больших моделей
Как определить количество слоев и нейронов скрытых слоев нейронной сети?


