Алгоритм двоичного дерева поиска C#
Бинарное дерево поиска (Двоичное Search Дерево (сокращенно BST) — это специальное двоичное дерево, обладающее следующими свойствами: для каждого узла дерева значения всех узлов его левого поддерева меньше значения его узла, а значения всех узлов в его правом поддереве меньше значения его узла. Все значения больше значения его узла. Эта структура данных очень распространена в информатике, поскольку она обеспечивает эффективный способ хранения и извлечения данных. В этой статье мы подробно рассмотрим алгоритмы реализации бинарных деревьев поиска в C#, включая создание дерева、вставлять、удалить、Такие операции, как поиск и перемещение.
Основные понятия о двоичных деревьях поиска
Прежде чем подробно обсуждать алгоритм, давайте сначала определим некоторые основные понятия двоичных деревьев поиска:
- Узел:Самая маленькая единица дерева,Содержит ключевое значение、указатель левого дочернего узла、Указатель правого дочернего узла.
- Корневой узел (Root):верхний узел дерева,Родительского узла нет.
- Поддерево:Дерево с корнем в узле。
- Листовой узел (Лист):Узел без дочерних узлов。
- Высота:Количество ребер на самом длинном пути от корневого узла до листового узла.。
- Баланс:Связь между высотой дерева и количеством узлов в дереве,Сбалансированные двоичные деревья поиска обеспечивают лучшую производительность.
C# реализация двоичного дерева поиска
Чтобы реализовать двоичное дерево поиска в C#, нам сначала нужно определить класс узла, а затем реализовать основные операции с деревом.
Определение класса узла
public class TreeNode
{
public int Value { get; set; }
public TreeNode Left { get; set; }
public TreeNode Right { get; set; }
public TreeNode(int value)
{
Value = value;
Left = null;
Right = null;
}
}создание дерева
Создание бинарного дерева поиска обычно начинается с пустого дерева, а затем вставляются узлы один за другим.
public class BinarySearchTree
{
public TreeNode Root { get; set; }
public BinarySearchTree()
{
Root = null;
}
}Вставка узлов
Операция вставки является ядром двоичного дерева поиска, которое должно поддерживать поисковую природу дерева. Временная сложность операции вставки равна O(h), где h — высота дерева.
public void Insert(int value)
{
Root = Insert(Root, value);
}
private TreeNode Insert(TreeNode node, int value)
{
if (node == null)
{
node = new TreeNode(value);
}
else if (value < node.Value)
{
node.Left = Insert(node.Left, value);
}
else if (value > node.Value)
{
node.Right = Insert(node.Right, value);
}
return node;
}Поиск узла
Операция поиска проверяет, существует ли значение в двоичном дереве поиска. Временная сложность операции поиска также равна O(h).
public bool Search(int value)
{
return Search(Root, value) != null;
}
private TreeNode Search(TreeNode node, int value)
{
if (node == null || node.Value == value)
{
return node;
}
if (value < node.Value)
{
return Search(node.Left, value);
}
return Search(node.Right, value);
}Удаление узла
Операция удаления является более сложной операцией в бинарном дереве поиска. Необходимо учитывать три ситуации: удаление конечных узлов, удаление узлов только с одним дочерним узлом и удаление узлов с двумя дочерними узлами.
public void Delete(int value)
{
Root = Delete(Root, value);
}
private TreeNode Delete(TreeNode node, int value)
{
if (node == null)
{
return node;
}
if (value < node.Value)
{
node.Left = Delete(node.Left, value);
}
else if (value > node.Value)
{
node.Right = Delete(node.Right, value);
}
else
{
if (node.Left == null)
{
return node.Right;
}
else if (node.Right == null)
{
return node.Left;
}
node.Value = FindMinValue(node.Right);
node.Right = Delete(node.Right, node.Value);
}
return node;
}
private int FindMinValue(TreeNode node)
{
while (node.Left != null)
{
node = node.Left;
}
return node.Value;
}обход дерева
Операция обхода заключается в посещении каждого узла дерева. Общие методы обхода включают обход в предварительном порядке, обход по порядку, обход после порядка и обход по уровню.
public void InOrderTraversal(Action<int> action)
{
InOrderTraversal(Root, action);
}
private void InOrderTraversal(TreeNode node, Action<int> action)
{
if (node != null)
{
InOrderTraversal(node.Left, action);
action(node.Value);
InOrderTraversal(node.Right, action);
}
}Оптимизация производительности бинарных деревьев поиска
Хотя деревья двоичного поиска обеспечивают эффективные операции с данными, в худшем случае (например, когда дерево сильно несбалансировано) его производительность снижается до O(n). Для оптимизации производительности мы можем рассмотреть следующие стратегии:
- Самобалансирующееся двоичное дерево поиска:нравитьсяAVLдерево или красно-черное дерево,Они поддерживают баланс дерева посредством вращательных операций.
- Разделение и слияние деревьев:существоватьвставлятьиудалить В эксплуатации,Поддерживайте баланс дерева, разделяя и объединяя поддеревья.
- Используйте таблицы переходов:Список переходов — это структура данных, основанная на связанном списке.,Он обеспечивает производительность, аналогичную сбалансированным двоичным деревьям поиска.,Но реализация проще.

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
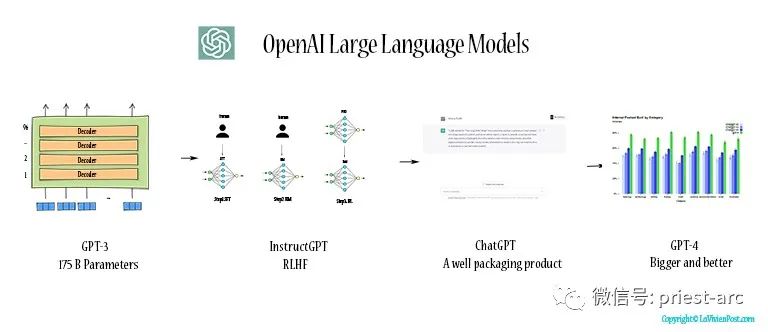
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
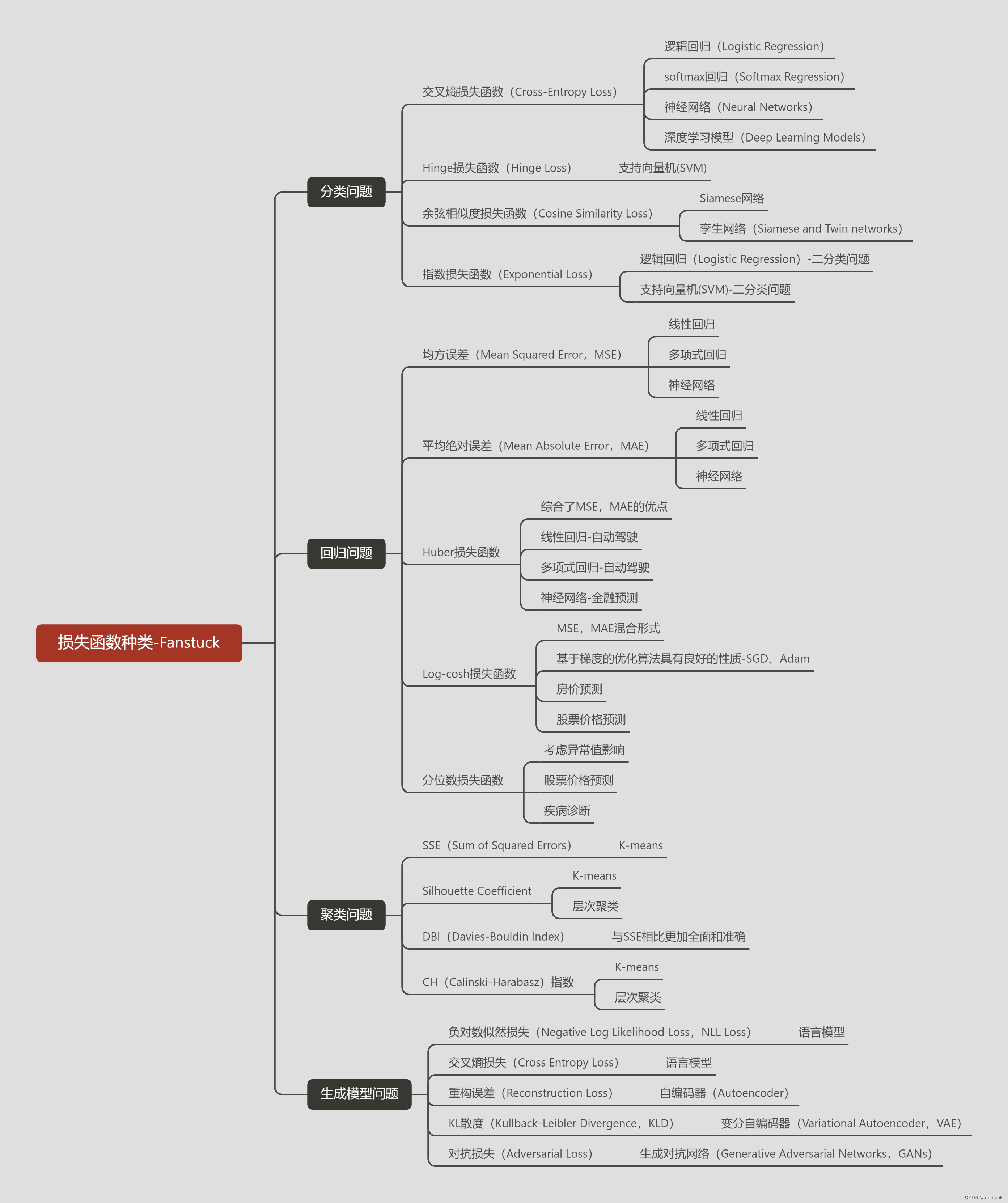
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
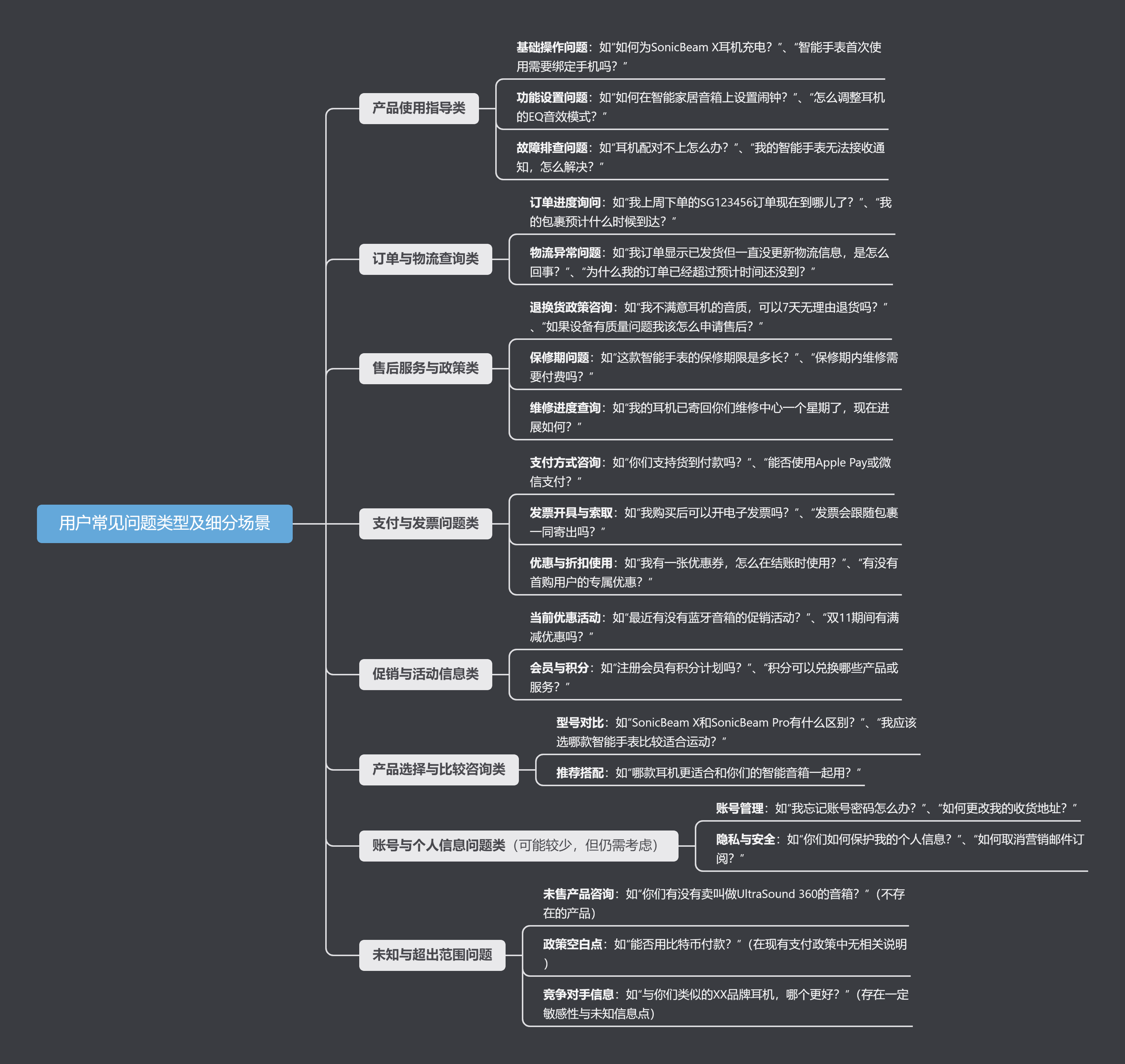
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
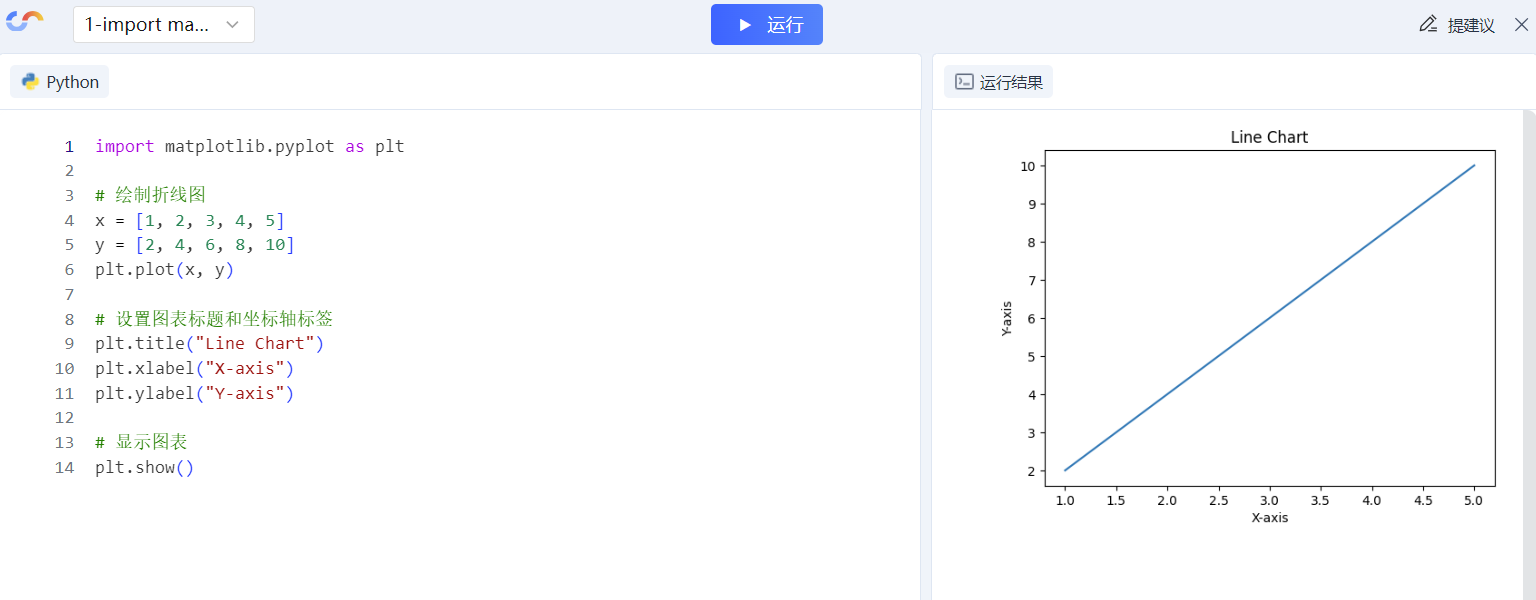
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
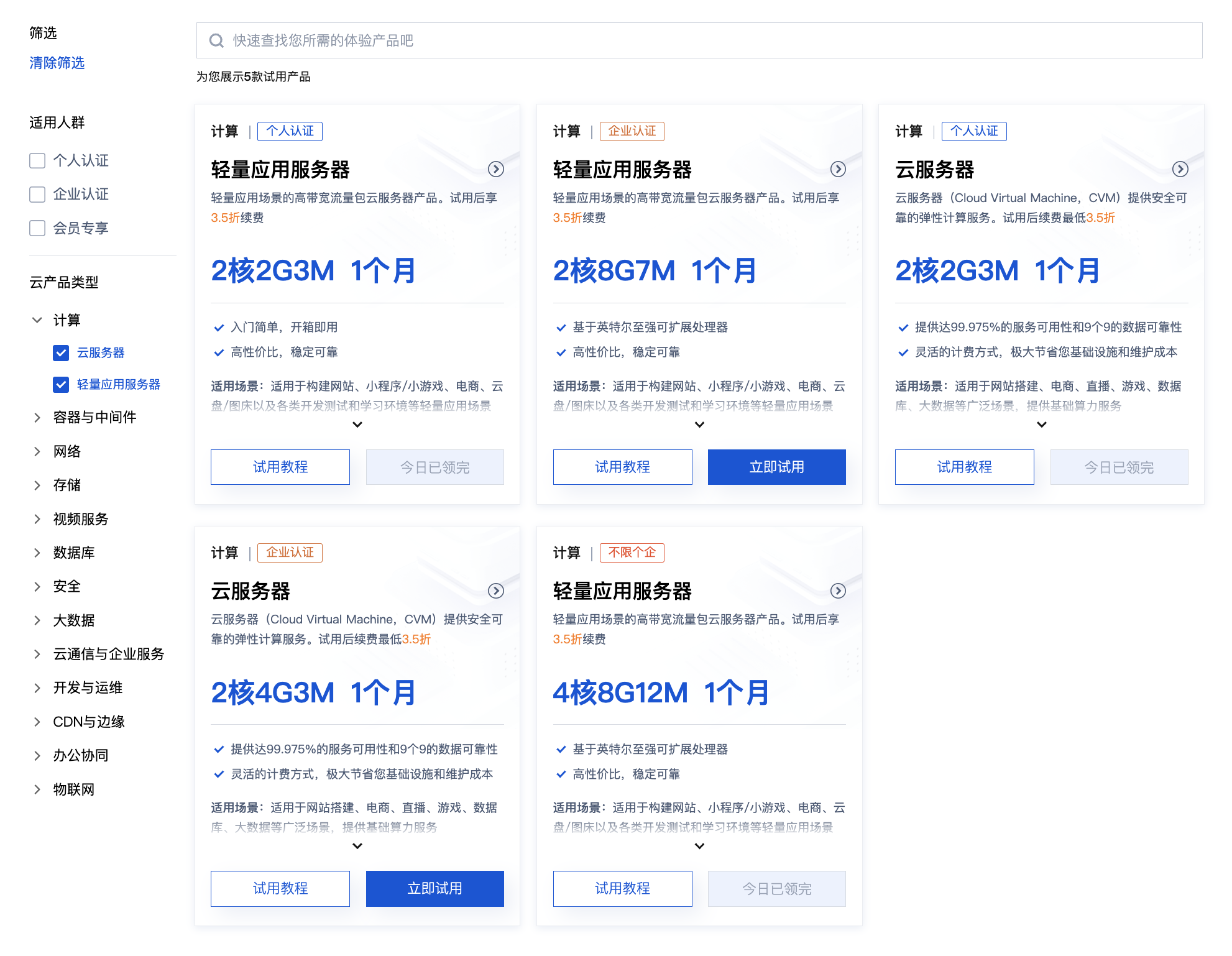
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.