1. Аналоговый фильтр Баттерворта (низкочастотный, высокочастотный, полосовой, полосовой заграждающий) — реализация MATLAB
Всем привет, мы снова встретились, я ваш друг Цюаньчжаньцзюнь.
Эта статья об аналоговых фильтрах.дизайн,Если вам нужно знать о цифровых фильтрах,Вы можете прочитать два других блога, которые я написал по порядку.,следующее:
2.MATLAB реализует цифровой фильтр с бесконечной импульсной характеристикой (БИХ).
3. MATLAB реализует цифровой фильтр с конечной импульсной характеристикой (FIR).
Оглавление
1. Введение в базовые знания
Давайте сначала уточним кое-что (это очень важно):
Синусоидальный сигнал частотой 50Гц. это означает Аналоговая частота сигнала f f f= 50 (Hz),Обратите внимание, что его единица измерения — Гц.
Выражение сигнала y знак равно s я п ( 2 π ж т ) знак равно s я п ( 2 π * 50 т ) знак равно s я п ( 100 π т ) y знак равно грех (2 \ пи фут) = грех (2 \ пи *50 т) = грех (100 \ пи т) ) y=sin(2πft)=sin(2π*50t)=sin(100πt)
Поскольку сигнал также можно выразить в виде y = s i n ( Ω t ) y = sin(\Omega t) y=sin(Ωt), поэтому здесь Ω = 2 π f = 100 π \Omega=2\pi f=100\pi Ω=2πf=100π
Вот Ω \Omega Ω даАналоговая угловая частота,Его единица измерения — рад/с.。
УведомлениеАналоговая угловая частота Ω \Omega Ω иАналоговая частота f f отношения Ω = 2 π f \Omega=2\pi f Ω=2πf
2. Введение функции
Сначала представим некоторые используемые функции MATLAB.
2.1 Кнопка – Определите порядок фильтра N и частоту среза 3 д Б wc.
[N,wc] = buttord(wp, ws, Rp, As, ‘s’) Входные параметры следующие:
Граница полосы пропускания Аналоговая частотаwp、граница стоп-зоны Аналоговая частотаws(Аналоговая угловая частота,Единица измерения: рад/с.)
Максимальное затухание в полосе пропусканияRp、Минимальное затухание в полосе задерживанияAs(Единица измерения: д Б.)
«s» относится к аналоговому фильтру. При проектировании цифрового фильтра параметр «s» отсутствует.
2.2 масло – Решите конкретные параметры B и A фильтра N-порядка. После решения B и A проектирование фильтра завершено.
[B,A] = butter(N, wc, ‘ftype’, ‘s’) - Аналоговый фильтрВходные параметры следующие:
N – Порядок фильтра
wc – 3dBКрайний срок Аналоговая частота(Единица измерения рад/с,N и wc рассчитываются с использованием функции Buttord)
ftype – Тип фильтра '': (1)Когда входной сигнал wc является одномерным вектором: по умолчаниюслучайдизайнизнизкий проходфильтр,дизайнКвалкоммфильтриз话令ftype=high
(2)Когда входной сигнал wc является двумерным вектором [wcl,wcu]: по умолчаниюслучайдизайнизполосовой пропускфильтр,дизайнполосовое сопротивлениефильтриз话令ftype=stop
2.3 фильтр – функция фильтра
y = filter(B,A,x)Это функция фильтра,
x — входной шумовой сигнал,
B и A — расчетные параметры фильтра.
Полученный выходной сигнал y является отфильтрованным сигналом.
3. Реализация кода:
(1) Фильтр нижних частот:
пример: Спроектируйте фильтр нижних частот Баттерворта с частотой среза полосы пропускания 5 к Гц, затуханием в полосе пропускания 2 д Б, частотой среза полосы задерживания 12 к Гц и затуханием в полосе задерживания 30 д Б.
Как видно из вопроса, конструкция представляет собой аналоговый фильтр, поэтому используются следующие три функции:
[N,wc] = buttord(wp, ws, Rp, As, ‘s’)
[B,A] = butter(N, wc, ‘ftype’, ‘s’)
y = filter(B,A,x)Сосредоточиться на ! ! !:
Все частоты аналоговых фильтров являются аналоговыми угловыми частотами. Ω \Omega Ω , оно и частота f f f отношение Ω = 2 π f \Omega = 2\pi f Ω=2πf
Итак, здесь
wp = 2 ∗ p i ∗ 5000 2*pi*5000 2∗pi∗5000,ws = 2 ∗ p i ∗ 12000 2*pi*12000 2∗pi∗12000,Rp = 2, As = 30
Код выглядит следующим образом:
wp = 2 * pi * 5000;
ws = 2 * pi * 12000;
Rp = 2;
As = 30;
[N, wc] = buttord(wp, ws, Rp, As, 's');
[B, A] = butter(N, wc, 's');Приведенные выше коды проектируют фильтр.
Если есть входной шумовой сигнал x, вызовите y = filter(B,A,x), и полученный y будет отфильтрованным сигналом.
Ниже представлена часть чертежа
Чтобы придать результатам фильтра более наглядное представление,Мы можем нарисовать его амплитудно-частотную характеристику.,Код выглядит следующим образом: Среди них мы использовали функцию частот,
h = freqs(B,A,wk)Он используется для расчета размера соответствующей частотной характеристики h, когда частота равна wk, и в основном используется для рисования изображений.
Рисунок Код выглядит следующим образом:
f = 0 : 10 : 14000;% снимает очки, от 0 до 14000, беря по очку каждые 10
w = 2 * pi * f;% Обратите внимание, что все частоты, используемые в аналоговых фильтрах, являются аналоговыми. угловая частота, умноженная на 2pi
Hk = freqs(B,A,w);%Для каждой взятой точки найдите там частотную характеристику.
%Рисовать
figure
plot(f/1000, 20 * log10(abs(Hk)));%Единица измерения по абсциссе – к Гц, по ординате – Единица. измерения: д Б.,
grid on;
%Установите метки горизонтальных и вертикальных координат
xlabel('f/kHz');
ylabel('-A(f)/dB');
%Установить диапазон горизонтальной и вертикальной оси
axis([0, 14, -40, 5]);Результаты розыгрыша следующие:

(2) Фильтр верхних частот:
Фильтр верхних частот практически аналогичен фильтру нижних частот, только обратите внимание. [B,A] = butter(N, wc, ‘ftype’, «с») в ftype=high
пример: Спроектируйте фильтр верхних частот Баттерворта с частотой среза полосы пропускания 4 к Гц, затуханием в полосе пропускания 0,1 д Б, частотой среза полосы задерживания 1 к Гц и затуханием в полосе задерживания 40 д Б.
Код выглядит следующим образом:
wp = 2 * pi * 4000;
ws = 2 * pi * 1000;
Rp = 0.1;
As = 40;
[N, wc] = buttord(wp, ws, Rp, As, 's');
[B, A] = butter(N, wc,'high', 's');%Обратите внимание на этот "высокий"Завершена разработка фильтра верхних частот.
Если есть входной шумовой сигнал x, вызовите y = filter(B,A,x), и полученный y будет отфильтрованным сигналом.
Затем рисуем амплитудно-частотную характеристику фильтра верхних частот
f = 0 : 10 : 14000;% снимает очки, от 0 до 14000, беря по очку каждые 10
w = 2 * pi * f;% Обратите внимание, что все частоты, используемые в аналоговых фильтрах, являются аналоговыми. угловая частота, умноженная на 2pi
Hk = freqs(B,A,w);%Для каждой взятой точки найдите там частотную характеристику.
%Рисовать
figure
plot(f/1000, 20 * log10(abs(Hk)));%Единица измерения по абсциссе – к Гц, по ординате – Единица. измерения: д Б.,
grid on;
%Установите метки горизонтальных и вертикальных координат
xlabel('f/kHz');
ylabel('-A(f)/dB');
%Установить диапазон горизонтальной и вертикальной оси
axis([0, 14, -60, 5]);График выглядит следующим образом:

(3) Полосовой фильтр:
пример: Спроектируйте полосовой фильтр Баттерворта с верхними и нижними граничными частотами полосы пропускания, составляющими 4 к Гц и 7 к Гц соответственно, затухание в полосе пропускания составляет 1 д Б, верхняя и нижняя граничные частоты полосы задерживания составляют 2 к Гц и 9 к Гц, а затухание в полосе задерживания составляет 20 д Б.
фильтрдизайн Код выглядит следующим образом:
%полосовой пропуск
wp = 2 * pi * [4000, 7000];
ws = 2 * pi * [2000,9000];
Rp = 1;
As = 20;
[N, wc] = buttord(wp, ws, Rp, As, 's');%В этот момент входные данные wp и ws являются двумерными, а выходные данные wc также являются двумерными.
[B, A] = butter(N, wc,'s');Завершена разработка полосового аналогового фильтра.
Если есть входной шумовой сигнал x, вызовите y = filter(B,A,x), и полученный y будет отфильтрованным сигналом.
Затем рисуем амплитудно-частотную характеристику полосового фильтра следующим образом:
f = 0 : 10 : 14000;% снимает очки, от 0 до 14000, беря по очку каждые 10
w = 2 * pi * f;% Обратите внимание, что все частоты, используемые в аналоговых фильтрах, являются аналоговыми. угловая частота, умноженная на 2pi
Hk = freqs(B,A,w);%Для каждой взятой точки найдите там частотную характеристику.
%Рисовать
figure
plot(f/1000, 20 * log10(abs(Hk)));%Единица измерения по абсциссе – к Гц, по ординате – Единица. измерения: д Б.,
grid on;
%Установите метки горизонтальных и вертикальных координат
xlabel('f/kHz');
ylabel('-A(f)/dB');
%Установить диапазон горизонтальной и вертикальной оси
axis([0, 14, -60, 5]);График выглядит следующим образом:

(4) Полосовой фильтр:
пример: Спроектируйте полосовой заграждающий фильтр Баттерворта с верхними и нижними граничными частотами полосы пропускания 2 к Гц и 9 к Гц соответственно, затуханием в полосе пропускания 1 д Б, верхней и нижней граничными частотами полосы задерживания 4 к Гц и 7 к Гц и затуханием в полосе задерживания 20 д Б.
%полосовое сопротивление
wp = 2 * pi * [2000, 9000];
ws = 2 * pi * [4000,7000];
Rp = 1;
As = 20;
[N, wc] = buttord(wp, ws, Rp, As, 's');%В этот момент входные данные wp и ws являются двумерными, а выходные данные wc также являются двумерными.
[B, A] = butter(N, wc,'stop','s');
полосовое Разработка резисторного аналогового фильтра завершена, если есть входной шумовой сигнал x, вызовите
y = filter(B,A,x), полученное значение y является отфильтрованным сигналом.Затем рисуем полосовое Амплитудно-частотная характеристика резистивного фильтра, Код выглядит следующим образом:
f = 0 : 10 : 14000;% снимает очки, от 0 до 14000, беря по очку каждые 10
w = 2 * pi * f;% Обратите внимание, что все частоты, используемые в аналоговых фильтрах, являются аналоговыми. угловая частота, умноженная на 2pi
Hk = freqs(B,A,w);%Для каждой взятой точки найдите там частотную характеристику.
%Рисовать
figure
plot(f/1000, 20 * log10(abs(Hk)));%Единица измерения по абсциссе – к Гц, по ординате – Единица. измерения: д Б.,
grid on;
%Установите метки горизонтальных и вертикальных координат
xlabel('f/kHz');
ylabel('-A(f)/dB');
%Установить диапазон горизонтальной и вертикальной оси
axis([0, 14, -100, 5]);Результат следующий:

Издатель: Лидер стека программистов полного стека, укажите источник для перепечатки: https://javaforall.cn/145891.html Исходная ссылка: https://javaforall.cn

Углубленный анализ переполнения памяти CUDA: OutOfMemoryError: CUDA не хватает памяти. Попыталась выделить 3,21 Ги Б (GPU 0; всего 8,00 Ги Б).
[Решено] ошибка установки conda. Среда решения: не удалось выполнить первоначальное зависание. Повторная попытка с помощью файла (графическое руководство).
Прочитайте нейросетевую модель Трансформера в одной статье

.ART Теплые зимние предложения уже открыты

Сравнительная таблица описания кодов ошибок Amap

Уведомление о последних правилах Points Mall в декабре 2022 года.

Даже новички могут быстро приступить к работе с легким сервером приложений.
Взгляд на RSAC 2024|Защита конфиденциальности в эпоху больших моделей
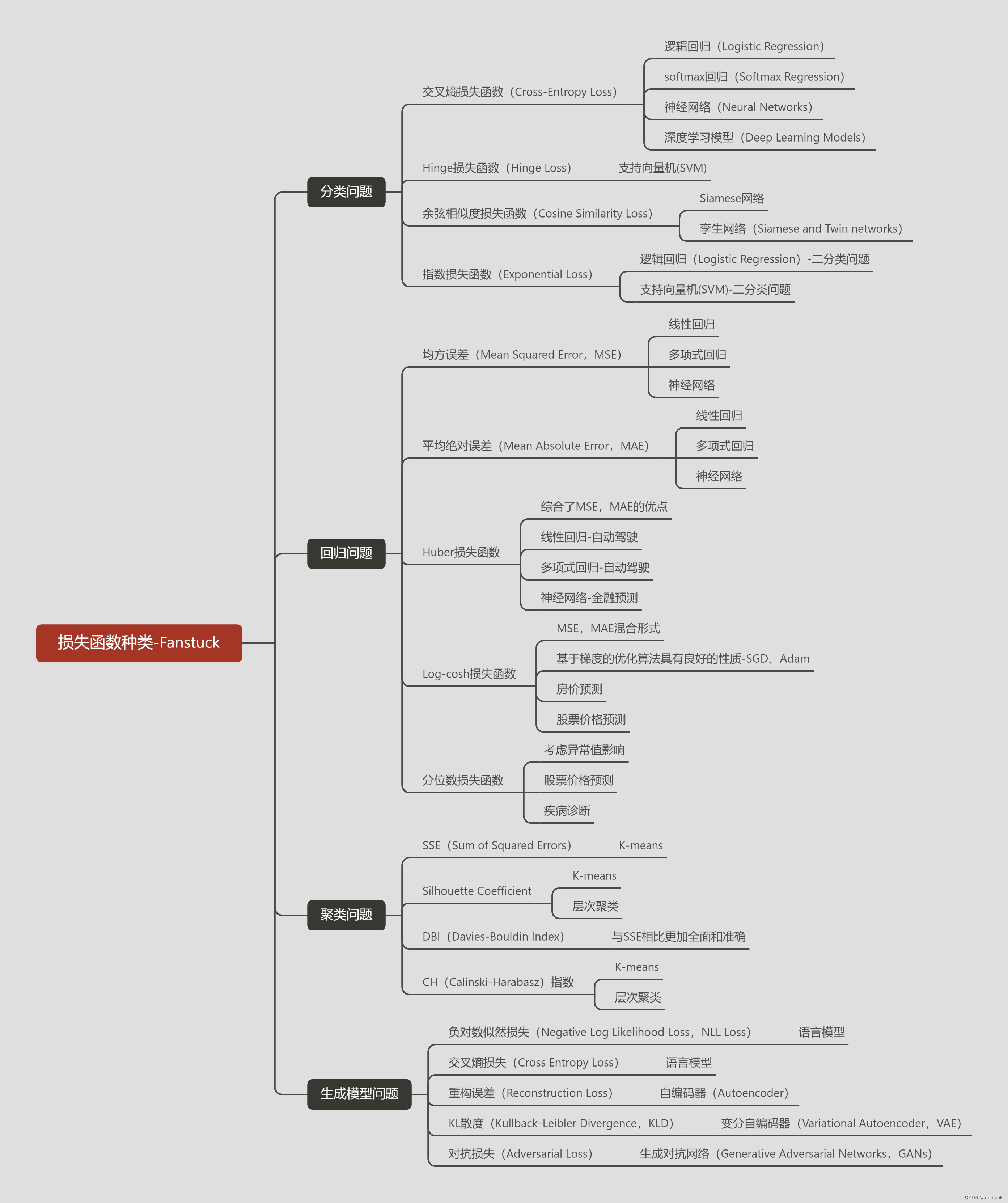
Вы используете ИИ каждый день и до сих пор не знаете, как ИИ дает обратную связь? Одна статья для понимания реализации в коде Python общих функций потерь генеративных моделей + анализ принципов расчета.

Используйте (внутренний) почтовый ящик для образовательных учреждений, чтобы использовать Microsoft Family Bucket (1T дискового пространства на одном диске и версию Office 365 для образовательных учреждений)
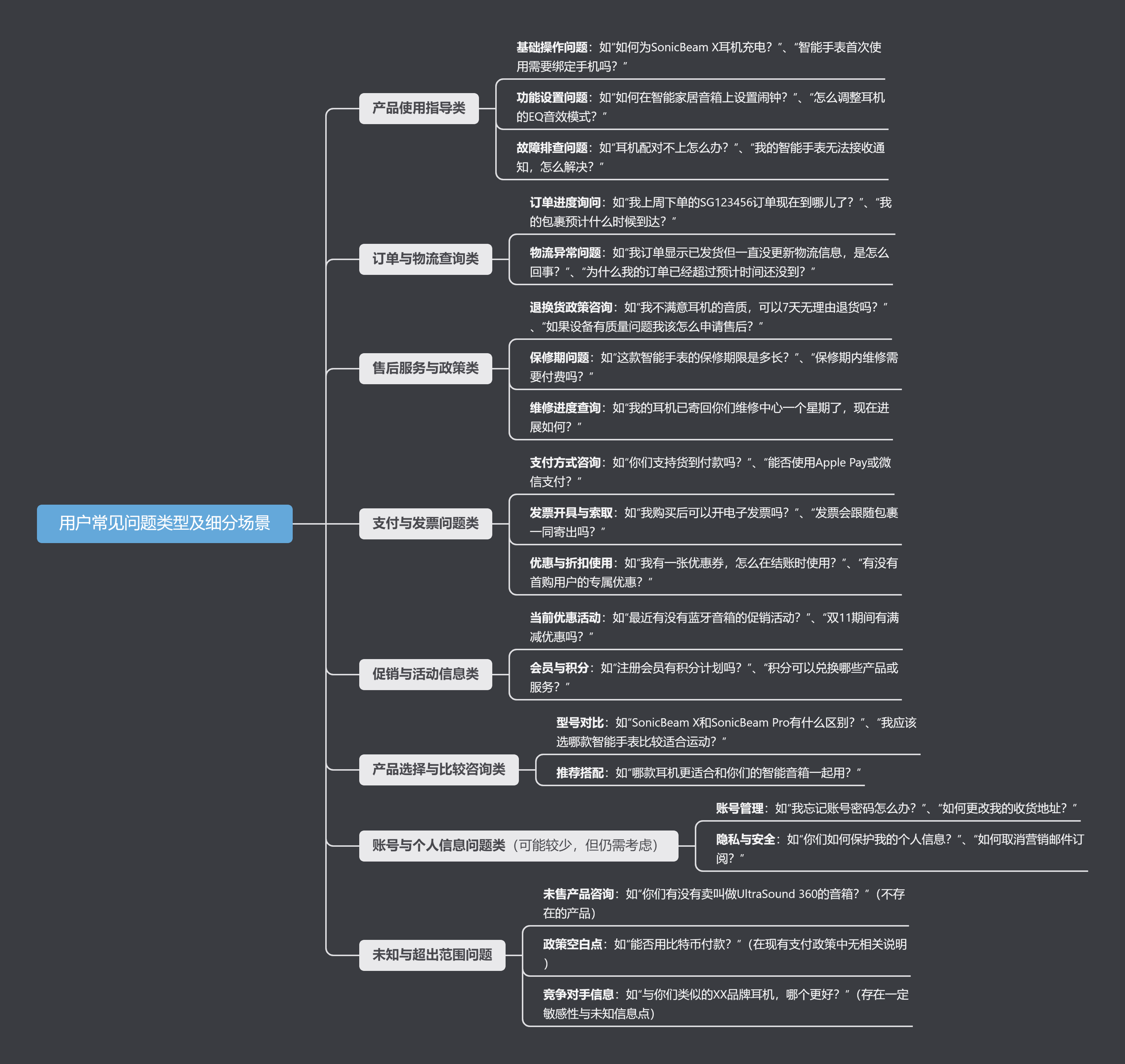
Руководство по началу работы с оперативным проектом (7) Практическое сочетание оперативного письма — оперативного письма на основе интеллектуальной системы вопросов и ответов службы поддержки клиентов

[docker] Версия сервера «Чтение 3» — создайте свою собственную программу чтения веб-текста

Обзор Cloud-init и этапы создания в рамках PVE

Корпоративные пользователи используют пакет регистрационных ресурсов для регистрации ICP для веб-сайта и активации оплаты WeChat H5 (с кодом платежного узла версии API V3)

Подробное объяснение таких показателей производительности с высоким уровнем параллелизма, как QPS, TPS, RT и пропускная способность.
Удачи в конкурсе Python Essay Challenge, станьте первым, кто испытает новую функцию сообщества [Запускать блоки кода онлайн] и выиграйте множество изысканных подарков!

[Техническая посадка травы] Кровавая рвота и отделка позволяют вам необычным образом ощипывать гусиные перья! Не распространяйте информацию! ! !

[Официальное ограниченное по времени мероприятие] Сейчас ноябрь, напишите и получите приз

Прочтите это в одной статье: Учебник для няни по созданию сервера Huanshou Parlu на базе CVM-сервера.

Cloud Native | Что такое CRD (настраиваемые определения ресурсов) в K8s?

Как использовать Cloudflare CDN для настройки узла (CF самостоятельно выбирает IP) Гонконг, Китай/Азия узел/сводка и рекомендации внутреннего высокоскоростного IP-сегмента

Дополнительные правила вознаграждения амбассадоров акции в марте 2023 г.
Можно ли открыть частный сервер Phantom Beast Palu одним щелчком мыши? Супер простой урок для начинающих! (Прилагается метод обновления сервера)
[Играйте с Phantom Beast Palu] Обновите игровой сервер Phantom Beast Pallu одним щелчком мыши

Maotouhu делится: последний доступный внутри страны адрес склада исходного образа Docker 2024 года (обновлено 1 декабря)

Кодирование Base64 в MultipartFile

5 точек расширения SpringBoot, супер практично!

Глубокое понимание сопоставления индексов Elasticsearch.